元素逆置

• 概述：其实就是将 第一个元素和最后一个元素交换，第二个元素和倒数第二个元素交换，依次到中间位置。
• 用途：可用于数组的移动，字符串反转，链表反转操作，栈和队列反转等操作。

逆置图解

代码

// 逆置元素算法
void Reverse(int R[] , int l , int r){// R 数组，l 左边 r 右边int i , j ,temp;for(i=l , j=r; i < j; i++,j--){					// i < j 不过数组个数是奇数还是偶数都行temp = R[i];R[i] = R[j];R[j] = temp;}
}

注意：逆置算法很简单，但是能延申其他的算法

---

循环移动算法

• 考研常考的一个算法，结合逆置算法，可进行实现

循环左移(右移)算法

图解

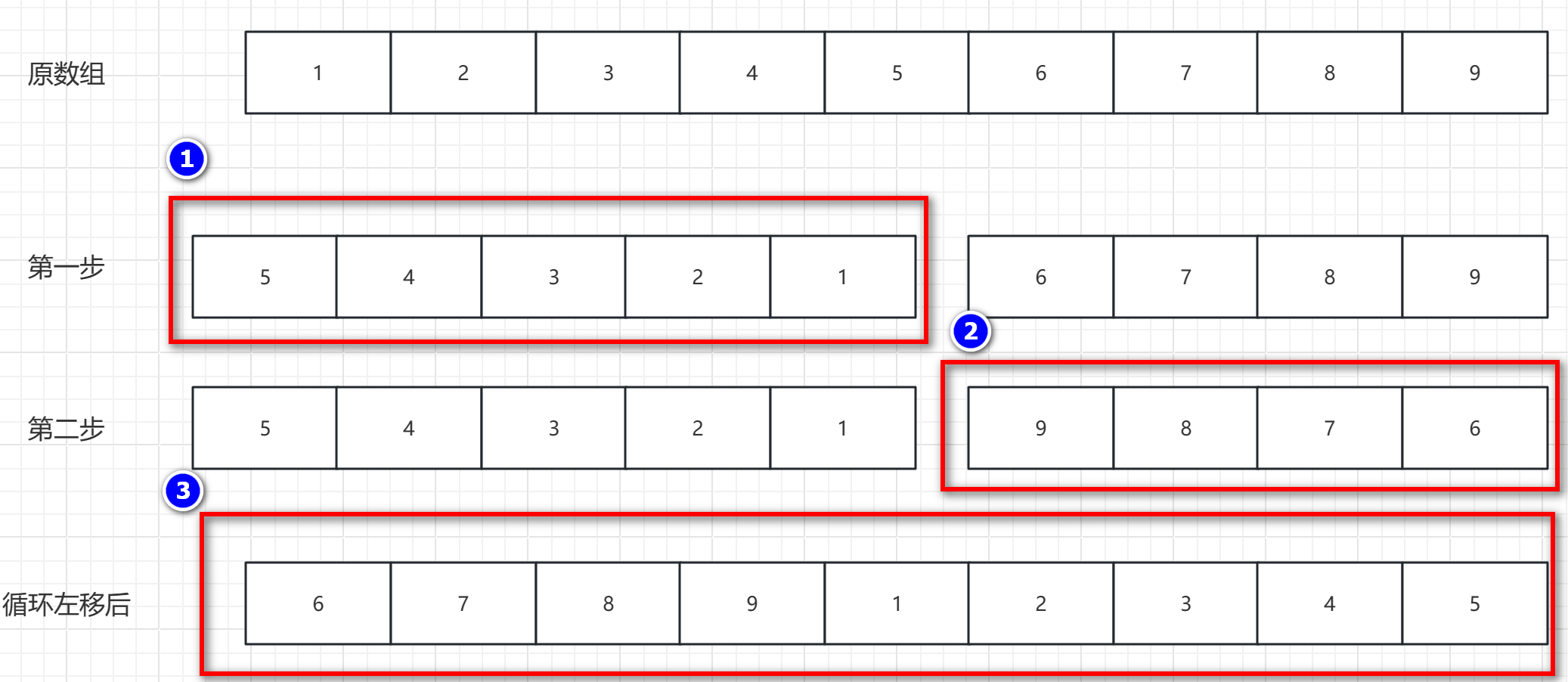
• 第一步：循环左移 p 个元素，就将 数组前 p 个（0~p-1）元素先进行逆置
• 第二步：再将 数组 p-1位置 之后的（n-p）个元素进行逆置
• 第三步：将 整个数组 整体进行逆置，即可得到 循环左移 p 个元素

代码

// 逆置元素算法
void Reverse(int R[] , int l , int r){// R 数组，l 左边 r 右边int i , j ,temp;for(i=l , j=r; i < j; i++,j--){temp = R[i];R[i] = R[j];R[j] = temp;}
}
// 循环左移算法
void LeftMove(int R[] , int n , int p){// r 数组 n 数组元素个数 p 循环左移个数if(p<0 || p>n){cout <<"ERROR"<<endl; }else{Reverse(r , 0 , p-1);        // 先逆置前p个Reverse(r , p , n-1);        // 再逆置后n-p个Reverse(r , 0 , n-1);        // 最后再把所有的都逆置}
}

时间复杂度分析

①：第一行 Reverse 执行频度为：1 + (p-1-0+1)/2
②：第二行 Reverse 执行频度为：1 + (n-1-p+1)/2
③：第三行 Reverse 执行频度为：1 + (n-1-0+1)/2
f(n) = 3 + n
T(n) = O(f(n)) = O(n)

空间复杂度

由于可以看到在 整个算法中，我们只定义了变量，并未定义其他数据结构，也未使用递归，所以空间复杂度是常数级别。为 O(1)