前缀和
S [ i ] = Σ i j = 1 A [ j ] = S [ i − 1 ] + A [ i ] \text{S}\left[ \text{i} \right] =\underset{\text{j}=1}{\overset{\text{i}}{\Sigma}}\text{A}\left[ \text{j} \right] =\text{S}\left[ \text{i}-1 \right] +\text{A}\left[ \text{i} \right] S[i]=j=1ΣiA[j]=S[i−1]+A[i]
说白了: S[i]就是前i项相加
- 子段和
sum(l,r):从数组中第l数计算到第r个数的和。----- 也就是部分和,从l项累加到r项
sum ( l,r ) = S [ r ] − S [ l − 1 ] \text{sum}\left( \text{l,r} \right) =\text{S}\left[ \text{r} \right] -\text{S}\left[ \text{l}-1 \right] sum(l,r)=S[r]−S[l−1]
为了不用分类讨论,一般设置前缀和数组第一个元素为0,这样:nums[0]=pre[0+1]-pre[0]可得到
前缀和的类实现
class preSum{
public:preSum(const vector<int>& nums){pre.push_back(0);int n = nums.size(); for (int i = 1;i<=n;i++){//注意:如果没添加过pre[i],是不可以直接下标访问的pre.push_back(nums[i-1] + pre[i - 1]);}}int sumRange(int i,int j){//求:nums中[i,j]区间的和//0 nums[0] nums[0]+nums[1] nums[0]+nums[1]+nums[2] ....//如果是1开始,[i,j]和:pre[j]-pre[i-1],现在添加了0return pre[j+1] - pre[i];}int numsVal(int i){return sumRange(i, i);//return pre[i + 1] - pre[i];}void traverse(){for(auto val:pre){cout << val << " ";}cout << endl;}
private:vector<int> pre;
};
注意:[i,j]之间的和:包含j且j最大的和-不包含i且i-1最大的和
力扣53:求出连续和最大值
class Solution {
public:int maxSubArray(vector<int>& nums) {//建立nums的前缀和数组preint n=nums.size();vector<int> pre(n+1);for(int i=1;i<=n;i++)pre[i]=pre[i-1]+nums[i-1];//对于i从1——n,考虑每一个j:求max(pre[i]-pre[j-1])//优化:只要求出pre[j-1]最小值即可int ret=-100000000;int premin=pre[0];for(int i=1;i<=n;i++){ret=max(ret,pre[i]-premin);premin=min(premin,pre[i]);}return ret;}
};
//法二:直接记录前i-1个数的和的最小值
int maxSubArray(vector<int>& nums) {//建立nums的前缀和数组preint n=nums.size();vector<int> pre(n+1);for(int i=1;i<=n;i++)pre[i]=pre[i-1]+nums[i-1];//求前缀最小值:前i个数和的最小值是fix[i]vector<int> fix(n+1,0);fix[0]=pre[0];//这里其实就是遍历pre[i],记录最小的for(int i=1;i<=n;i++)fix[i]=min(pre[i],fix[i-1]);int ret=INT_MIN;int premin=pre[0];for(int i=1;i<=n;i++){//[j,i],求:pre[i]-pre[j-1]最小值//优化pre[i]-pre[j]最小,j<i//fix[i-1]就是[0,i-1]范围内前缀和最小即pre[j]ret=max(ret,pre[i]-fix[i-1]);}return ret;}
vector中resize()
resize(尺寸大小,多余的补充数值)
- 该函数是少删多补,如果尺寸小于原数组大小就删去原数组的值
- 如果尺寸大小多于原数组就补充第二个元素,默认为0
vector<int> nums = {1, 2, 3, 4, 5, 6, 7, 8, 9};nums.resize(7,9); //1 2 3 4 5 6 7nums.resize(3);//123nums.resize(12); //1 2 3 4 5 6 7 8 9 0 0 0nums.resize(12,10); //1 2 3 4 5 6 7 8 9 10 10 10
resize()改写,就可以pre[i]访问
preSum(const vector<int>& nums){int n = nums.size();pre.resize(n + 1);for (int i = 1;i<=n;i++){pre[i]=nums[i-1] + pre[i - 1];}}
vector初始化
同resize(): vector vec(n,m)----n个m值,默认为0
vector<int> aa(10, 22);vector<int> bb(7);
/*
22 22 22 22 22 22 22 22 22 22
0 0 0 0 0 0 0
*/
赋值,括号或者=
vector<int> aa = {1, 2, 3, 4, 5};vector<int> bb(aa);vector<int> cc = aa;
//12345
迭代器或指针
vector<int> aa = {1, 2, 3, 4, 5};vector<int> bb(aa.begin() + 1, aa.end() - 1);traverse(bb);//2,3,4 [,)
insert()
在给定位置前面插入元素,函数返回值是指向新加入元素的最前位置
vector<int> aa = {1, 2, 3};auto it = aa.insert(aa.begin(), 100);//100,1,2,3cout << *it << " ";//100 vector<int> aa = {1, 2, 3};auto it = aa.insert(aa.end(), 100);//1,2,3,100cout << *it << " ";//100vector<int> aa = {1, 2, 3};auto it = aa.insert(aa.end()-2,3,77);//1,(77,77,77),2,3cout << *it << " ";//77vector<int> aa = {1, 2, 3};vector<int> bb = {7, 8, 9};auto it = aa.insert(aa.end() - 1, bb.begin(), bb.end()); // 1,2,(7,8,9),3cout << *it << " "; // 7vector<int> aa = {1, 2, 3};int bb[3] = {7, 8, 9};auto it = aa.insert(aa.begin()+1, begin(bb), end(bb)); // 1,(7,8,9),2,3cout << *it << " "; // 7
测试:
vector<int> myvector(3, 100);vector<int>::iterator it;it = myvector.begin();it = myvector.insert(it, 200);
traverse(myvector);//(200),100,100,100myvector.insert(it, 2, 300);
traverse(myvector);//(300,300),200,100,100,100it = myvector.begin();std::vector<int> anothervector(2, 400);myvector.insert(it + 2, anothervector.begin(), anothervector.end());
traverse(myvector);//300,300,(400,400),200,100,100,100int myarray[] = {501, 502, 503};myvector.insert(myvector.begin(), myarray, myarray + 3);
traverse(myvector);//(501,502,503),300,300,400,400,200,100,100,100
原地前缀和:
vector<int> vec = {1, 2, 3, 4, 5, 6};// 原地改成前缀和vec.insert(vec.begin(), 0);for (int i = 1; i <= vec.size(); i++) {vec[i] += vec[i - 1];}
二维前缀和
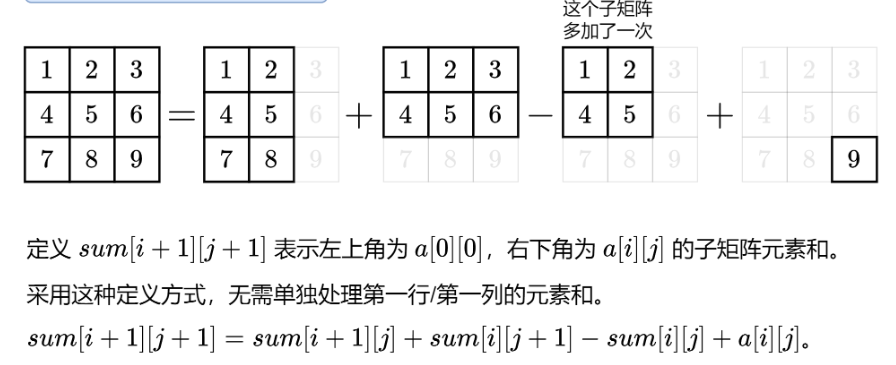
sum[i][j]:第i行和第j列构成的所有元素的和
相当于:sum[i-1][j]+sum[i][j-1]-sum[i-1][j-1]
即:去掉一行的和+去掉一列的和-去掉一行和一列的和(重叠部分)
然后加入当前下标元素值:a[i][j]
计算任意子矩阵和
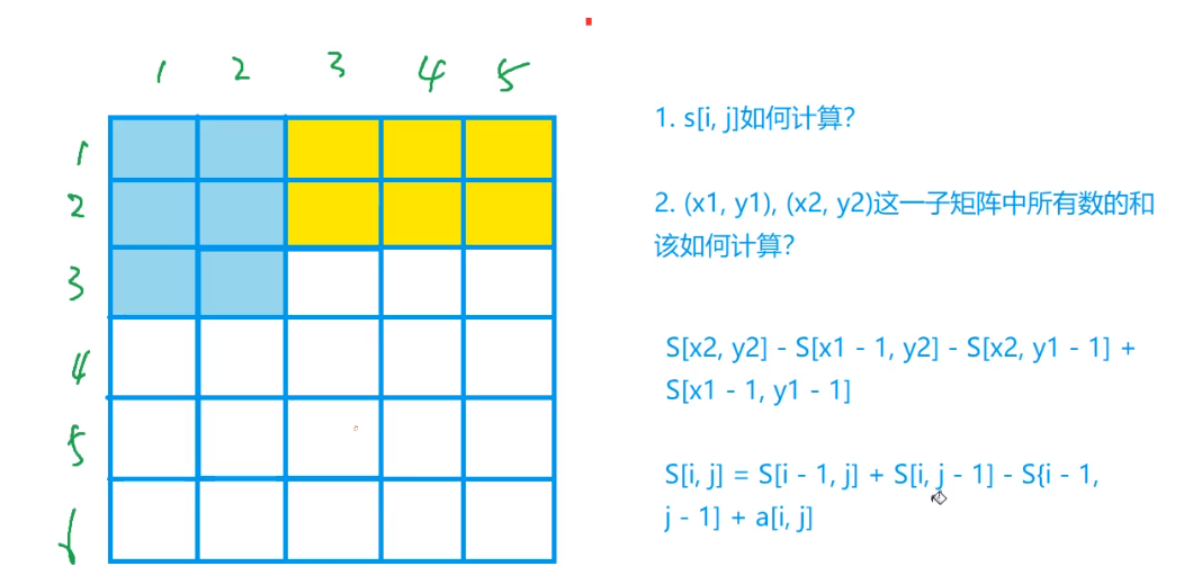
以(p,q)为左上角,(i,j)为右下角
设S[i,j]是(0,0)位置到(i,j)位置的和,a[i,j]是(i,j)位置上的值
sum(p,q,i,j)=sum[i] [j] - sum[i] [q-1]-sum[p-1] [j]+sum[p-1] [q-1]
这种方式可以用O(n平方)初始化前缀和矩阵,然后靠O(1)计算出结果
差分
差分是一种与
前缀和相对的策略,是求和的逆运算。
给定数组a i , 其差分数组为: \text{给定数组a}_{\text{i}},\text{其差分数组为:} 给定数组ai,其差分数组为:数组a = { a 1 , a 2 , a 3 , . . . , a n } \text{数组a}=\left\{ \text{a}_1,\text{a}_2,\text{a}_3,...,\text{a}_{\text{n}} \right\} 数组a={a1,a2,a3,...,an}
b i = { a 1 , i = 1 a i − a i − 1 2 ≤ i ≤ n \text{b}_{\text{i}}=\left\{ \begin{array}{l} \text{a}_1,\ \ \text{i}=1\\ \text{a}_{\text{i}}-\text{a}_{\text{i}-1}\ \ 2\le \text{i}\le \text{n}\\ \end{array} \right. bi={a1, i=1ai−ai−1 2≤i≤n
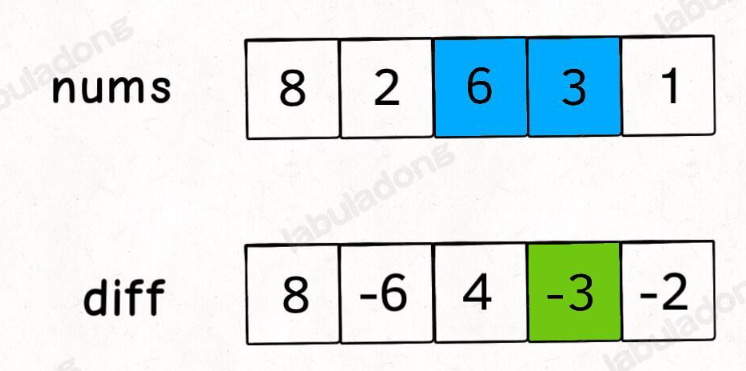
给定一个数组nums,其差分数组diff就是第一个元素不变,其余:diff[i]=nums[i]-nums[i-1] ( i>=1)
class diffSum{ // 差分
public://计算差分数组diffSum(const vector<int>& vec){diff.resize(vec.size());diff[0] = vec[0];for (int i = 1; i < diff.size();i++){diff[i] = vec[i] - vec[i - 1];}}//对差分数组求前缀和就是原数组vector<int> getOrigin(){vector<int> res;res.resize(diff.size());res[0] = diff[0];for (int i = 1; i < diff.size();i++){res[i] = res[i-1]+diff[i];//注意是已储存的res[i-1]}return res;};
private:vector<int> diff;
};
数组a = { a 1 , a 2 , a 3 , . . . , a n } , 差分数组b = { a 1 , a 2 − a 1 , a 3 − a 2 , . . . , a n − a n − 1 } \text{数组a}=\left\{ \text{a}_1,\text{a}_2,\text{a}_3,...,\text{a}_{\text{n}} \right\} ,\text{差分数组b}=\left\{ \text{a}_1,\text{a}_2-\text{a}_1,\text{a}_3-\text{a}_2,...,\text{a}_{\text{n}}-\text{a}_{\text{n}-1} \right\} 数组a={a1,a2,a3,...,an},差分数组b={a1,a2−a1,a3−a2,...,an−an−1}
发现:a i = Σ i j = 1 b j , 也就是说:差分数组的前缀和就是差分数组的原数组 \text{发现:a}_{\text{i}}=\underset{\text{j}=1}{\overset{\text{i}}{\Sigma}}\text{b}_{\text{j}},\text{也就是说:差分数组的前缀和就是差分数组的原数组} 发现:ai=j=1Σibj,也就是说:差分数组的前缀和就是差分数组的原数组
也就是说如果知道了该数组的差分数组后,对差分数组求前缀和,就可以得到原数组

差分应用
假如对数组a的 [ l,r ] 区间的每一个数加上一个数k: \text{假如对数组a的}\left[ \text{l,r} \right] \text{区间的每一个数加上一个数k:} 假如对数组a的[l,r]区间的每一个数加上一个数k:
{ a l + k,a l + 1 + k,a l + 2 + k,...,a r + k } ————这样连续区间的操作 \left\{ \text{a}_{\text{l}}+\text{k,a}_{\text{l}+1}+\text{k,a}_{\text{l}+2}+\text{k,...,a}_{\text{r}}+\text{k} \right\} \text{————这样连续区间的操作} {al+k,al+1+k,al+2+k,...,ar+k}————这样连续区间的操作
数组a = { a 1 , a 2 , a 3 , . . . , a n } , 差分数组: { a l + k,a l + 1 , a l + 2 , . . . , a r , a r + 1 − k } \text{数组a}=\left\{ \text{a}_1,\text{a}_2,\text{a}_3,...,\text{a}_{\text{n}} \right\} ,\text{差分数组:}\left\{ \text{a}_{\text{l}}+\text{k,a}_{\text{l}+1},\text{a}_{\text{l}+2},...,\text{a}_{\text{r}},\text{a}_{\text{r}+1}-\text{k} \right\} 数组a={a1,a2,a3,...,an},差分数组:{al+k,al+1,al+2,...,ar,ar+1−k}
发现对原数组需要进行[l,r]的操作,但是在差分数组只需要对l和r+1位置做出改变,这样在效率上会提高
class diffSum{ // 差分
public://原数组进行了区间操作,差分数组两端改变void op(int l,int r,int val){diff[l] += val;if(r+1<diff.size()){diff[r + 1] -= val;}}
private:vector<int> diff;
};
//主程序测试vector<int> vec = {1, 5, 3, 7, 2, 8, 4};diffSum mm(vec);//mm是vec差分数组int l = 2, r = 5,val=7;for (int i = l; i <= r;i++)vec[i] += 7;mm.op(l, r, val);vector aa = mm.getOrigin();//做前缀和for(auto v:aa)cout << v << " ";cout << endl;
)





-- 算法导论14.3 2题)






![机器人抓取 [ 题目/摘要 ] 更新中..](http://pic.xiahunao.cn/机器人抓取 [ 题目/摘要 ] 更新中..)





