原文链接：https://browse.arxiv.org/abs/2402.00752

1. 引言

许多基于3D高斯溅射（3D-GS）的方法针对稀疏视图场景的鲁棒性、性能和存储效率进行增强，但没有专门处理高斯投影的误差。

3D-GS以一组图像和相机通过SfM校准产生的点云为输入，建立3D高斯来表达场景。渲染时，3D高斯会通过投影函数$\varphi$投影到图像平面（$z=1$平面），以进行可微栅格化。

但是，尽管高斯函数经过卷积或仿射变换可以保留高斯属性，经过投影变换却不一定。因此，3D高斯溅射使用了局部仿射近似，即使用二阶泰勒展开近似投影函数，这会引入误差，从而在渲染图像中产生伪影。本文通过对泰勒余项的分析，揭示了3D高斯溅射误差与高斯均值的关系；同时，通过确定误差函数的极值，找到了使误差最小的条件。

本文还通过对误差函数的极值分析，提出最优投影方法，沿高斯均值与相机中心投影，投影平面与该线垂直。与直接将3D高斯投影到$z=1$平面相比，本文的投影方法误差更小，且也可实现真实且实时的渲染。

3. 准备知识

设有3D高斯函数$G$，由均值$\mu$和协方差矩阵$\Sigma$表达：
$$G_{\mu ,\Sigma }(x)=\exp (-1/2(x-\mu {)}^T{\Sigma }^{-1}(x-\mu ))$$

在混合过程中，高斯会乘以不透明度$\alpha$。

通过视图变换矩阵$W$，将高斯函数从世界坐标系变换到相机坐标系：
$$G^{\prime }(x)=\exp (-1/2(Wx-W\mu {)}^T(W\Sigma W^T{)}^{-1}(Wx-W\mu ))\text{\hspace{1em}(1)}$$

记$x^{\prime }=Wx,{\mu }^{\prime }=W\mu ,{\Sigma }^{\prime }=W\Sigma W^T$，可得：
$$G^{\prime }(x^{\prime })=\exp (-1/2(x^{\prime }-{\mu }^{\prime }{)}^T{\Sigma }^{\prime -1}(x^{\prime }-{\mu }^{\prime }))$$

记$x_0=[0,0,1{]}^T$，$z=1$的投影平面可以记为：
$$x_0^T\cdot (x^{\prime }-x_0)=0$$

可以据此获取投影函数$\varphi$：
$$\varphi (x^{\prime })=x^{\prime }(x_0^T{x}^{\prime }{)}^{-1}(x_0^T{x}_0)=x^{\prime }(x_0^T{x}^{\prime }{)}^{-1}$$

可以使用泰勒展开到一阶：
$$\varphi (x^{\prime })=\varphi ({\mu }^{\prime })+\frac{\partial \varphi }{\partial x^{\prime }}({\mu }^{\prime })(x^{\prime }-{\mu }^{\prime })+R_1(x^{\prime })$$

其中$\frac{\partial \varphi }{\partial x^{\prime }}({\mu }^{\prime })$为投影变换的仿射近似，记为$J$。不考虑泰勒余项时，可按照(1)式类似推导得到投影的2D高斯：
$$\begin{array}{rl}{G}_{2D}(x^{\prime })& =\exp (-1/2(J{x}^{\prime }-J{\mu }^{\prime }{)}^T(J\Sigma J^T{)}^{-1}(J{x}^{\prime }-J{\mu }^{\prime }))\\ & \approx \exp (-1/2(\varphi (x^{\prime })-\varphi ({\mu }^{\prime }){)}^T(J\Sigma J^T{)}^{-1}(\varphi (x^{\prime })-\varphi ({\mu }^{\prime })))\end{array}$$

注意$J$的秩为2，$J\Sigma J^T$的逆跳过第三维度求取。记$x_{2D}=\varphi (x^{\prime }),{\mu }_{2D}=\varphi ({\mu }^{\prime }),{\Sigma }_{2D}=J{\Sigma }^{\prime }{J}^T$，则投影的2D高斯可写成：
$$G_{2D}(x_{2D})=\exp (-1/2(x_{2D}-{\mu }_{2D}{)}^T{\Sigma }_{2D}^{-1}(x_{2D}-{\mu }_{2D}))$$

4. 局部仿射近似误差

该部分推导见原文。

局部仿射近似误差由泰勒余项决定。可知该余项向量与随机变量$x^{\prime }$和高斯均值${\mu }^{\prime }$相关。可计算其F-范数的平方，并计算其关于$x^{\prime }$的期望，得到关于${\mu }^{\prime }$的误差函数$ϵ$。

然后，可以证明$x^{\prime }$与${\mu }^{\prime }$在单位球面上的投影 再投影到投影平面上（注意这个投影不是正交投影）时，得到的结果与直接将$x^{\prime }$和${\mu }^{\prime }$投影到投影平面上相同，即$(\varphi \circ \pi )(x^{\prime })=\varphi (x^{\prime })$。计算球面坐标，带入误差函数的表达式，可计算得到，当$x_0$与${\mu }^{\prime }$在球面上的投影重合时，误差函数取得极值。

可视化误差函数发现，极值附近的较大区域，误差函数值变化不大，但靠近积分界限时误差急剧变大。因此，使用局部仿射近似的3D-GS在多数情况下能高质量地合成新视图，但对于离平面中心（相机中心在投影面上的投影点）远的高斯，会有大误差，从而导致伪影。

5. 最优高斯溅射

5.1 最优投影

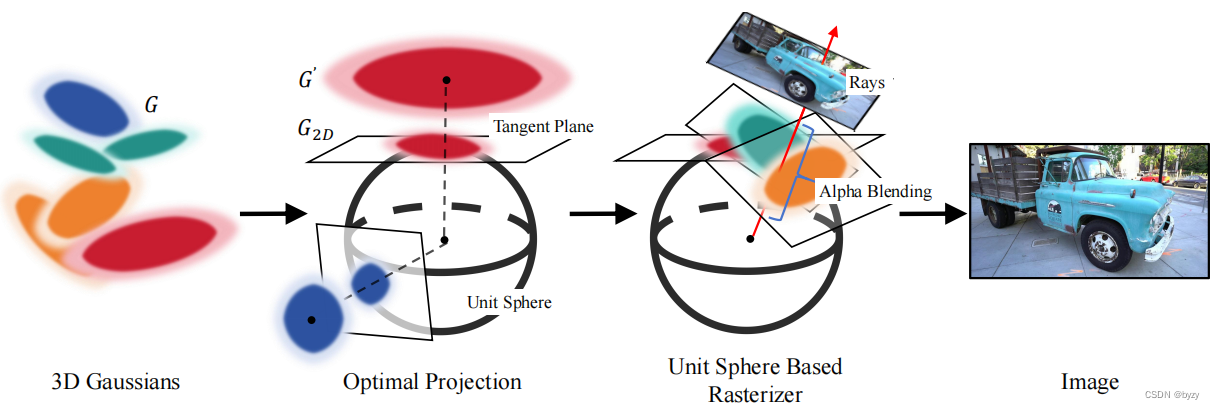
本文将各3D高斯投影到不同的平面（高斯均值的与相机中心连线的垂直平面）上，以保证投影误差最小。投影平面与单位球相切，为：
$$x^{\mu T}\cdot (x^{\prime }-x^{\mu })=0$$

其中$x^{\mu }=\pi ({\mu }^{\prime })={\mu }^{\prime }({\mu }^{\prime T}{\mu }^{\prime }{)}^{-1/2}$。最优投影函数为：
$${\varphi }^{\mu }(x^{\prime })=x^{\prime }(x^{\mu T}{x}^{\prime }{)}^{-1}$$

对应的局部仿射近似雅可比矩阵$J^{\mu }$可用${\mu }^{\prime }$的坐标表达（见原文）。

5.2 基于单位球的栅格化

由于投影不位于图像平面上，需要使用基于单位球的栅格化来生成图像。

具体来说，对图像像素$(u,v)$，类似NeRF投射射线，然后确定单位球上的哪些平面高斯与射线相交：
$$x_{2D}^{\mu }={\varphi }^{\mu }([(u-c_x)/f_x,(v-c_y)/f_y,1{]}^T)$$

然后使用$x_{2D}^{\mu }$查询高斯函数值，进行alpha混合，获取颜色：
$$C(u,v)=\sum _{z=z_{\text{near}}}^{z_{\text{far}}}\text{SH}({\mu }_z)\alpha (u,v,{\mu }_z)\prod _{k=z_{\text{near}}}^z(1-\alpha (u,v,{\mu }_k))$$

其中$\alpha (u,v,\mu )={\alpha }_{\mu }\cdot G_{2D}^{\mu }(x_{2D}^{\mu })$，${\alpha }_{\mu }$为中心为$\mu$的高斯的不透明度，$\text{SH}(\mu )$为中心为$\mu$的高斯的球面谐波，${\mu }_z$表示深度为$z$的高斯中心。

6. 实验

6.4 结果

定量结果：与MipNeRF360相比，本文方法在MipNeRF360数据集下PSNR性能略低，但速度远远更快。这是因为MipNeRF360没有使用显著的近似。但总的来说，与3D-GS和MipNeRF360相比，本文方法能保证实时性，并取得性能提升。

定性结果：与3D-GS相比，本文方法可以减少伪影产生并保留更多细节。