从一个问题开始

给定两个整数 n 和 k，返回 1 ... n 中所有可能的 k 个数的组合。

示例: 输入: n = 4, k = 2 输出: [ [2,4], [3,4], [2,3], [1,2], [1,3], [1,4] ]

很容易想到 用两个for循环就可以解决。

如果n为100，k为50呢，那就50层for循环，是不是开始窒息。

此时就会发现虽然想暴力搜索，但是用for循环嵌套连暴力都写不出来！

回溯法的本质

回溯的本质是穷举，穷举所有可能，然后选出我们想要的答案，如果想让回溯法高效一些，可以加一些剪枝的操作，但也改不了回溯法就是穷举的本质。

那么既然回溯法并不高效为什么还要用它呢？

因为没得选，一些问题能暴力搜出来就不错了，撑死了再剪枝一下(但最坏时间复杂度一般来说还是)，还没有更高效的解法。

搜索空间： 子集树

比如简单背包问题的解空间，本质就是一个满二叉树，只不过会通过剪枝避免暴力得出所有可能的解。

这里介绍的模版不会在求解时进行剪枝，因为本人认为这会让一个模版变得较为复杂，可能达到真正意义上的“通用性”，而是在获取到所有可能的解之后再按题目的要求进行筛选。

回溯法:0-1背包问题-CSDN博客

其中两个可行解为：

一个回溯法模版回顾

参考文章：代码随想录

void backtracking(参数) {if (终止条件) {存放结果;return;}for (选择：本层集合中元素（树中节点孩子的数量就是集合的大小）) {处理节点;backtracking(路径，选择列表); // 递归回溯，撤销处理结果}
}

 这个模版使用最大的难点就是如何写出终止条件，在递归过程中来存放结果往往会使得这个模版用起来较为困难。所以接下来介绍的模版是直接拿到所有的解之后再按条件进行筛选

暴力回溯法的模版

亮点在于容易写出来，缺点在回溯中没有用到剪枝，最好最坏时间复杂度都为

本质就是拿到一个高为N的树所有的叶子结点

import java.util.ArrayList;
import java.util.LinkedList;
import java.util.List;public class KnapsackProblem1 {static List<List<Integer>> result = new ArrayList<>();//path记录所有的可能,最后结果总共个数必定为2^Nstatic LinkedList<Integer> path = new LinkedList<>();//N代表着问题规模的大小,即2^N,最终的叶子结点个数就是2^Nstatic int N = 4;public static void main(String[] args) {backtracking();}public static void backtracking() {if (path.size() == N) {//找到了一个叶子结点，就保存下来//就算这个叶子结点是不满足题目的要求也保存下来result.add(new ArrayList<>(path));return;}//往1走代表选择这个元素path.add(1);backtracking();path.removeLast();//往0走代表不选择这个元素path.add(0);backtracking();path.removeLast();}
}

易于剪枝的回溯法模版应用

0-1背包问题

 问题描述

给定种物品和一背包。 物品的重量是， 其价值为，背包的容量为 c。 问应该如何选择装入背包中的物品，使得装入背包中物品的总价值最大？注意物品不重复!

实例：物品价值V={12, 11, 9, 8}, 物品重量W={8, 6, 4, 3}, 背包容量c=13

结点：向量 （ 子集的部分特征向量）

搜索空间： 子集树，片树叶

其中两个可行解为：

实现代码

终止条件代码

public static void backtracking(int n,  int startIndex) {if (startIndex>=n){//此时startIndex越界了if (getPathSum()<=c){result.add(new ArrayList<>(path));return;}return;}//再加后面任意一个就肯定不够了if (getPathSum()<=c&&(getPathSum() + items_min_weight[startIndex]) > c) {//        if (getPathSum()<c) {result.add(new ArrayList<>(path));return;}for (int i = startIndex; i < n; i++) {path.add(i);backtracking(n,  i + 1);path.removeLast();}

最终代码(含注释)

需要注意的是这里的可行，是再加上未选中的任意一项就>背包容量C

import java.util.ArrayList;
import java.util.LinkedList;
import java.util.List;public class KnapsackProblem {static List<List<Integer>> result = new ArrayList<>();static LinkedList<Integer> path = new LinkedList<>();static int N = 4;//    static int[] items_weight = new int[N];static int[] items_weight = {8, 6, 4, 3};//    static int[] items_value = new int[N];static int[] items_value = {12, 11, 9, 8};//每个items_min_weight(对应下标为i)的值为min{items_weight[i],...,items_weight[N-1]}static int[] items_min_weight = new int[N];//c为背包的容量static int c=13;public static void main(String[] args) {items_min_weight[N - 1] = items_weight[N - 1];int min = items_min_weight[N - 1];for (int i = items_weight.length - 2; i >= 0; i--) {if (items_weight[i] < min) {min = items_weight[i];}items_min_weight[i] = min;}backtracking(N,  0);System.out.println("可行解有:");result.forEach(System.out::println);//要是想求最优解,直接对每个可行解对应重量求和,之后取最大一个就好啦}public static void backtracking(int n,  int startIndex) {if (startIndex>=n){//此时startIndex越界了if (getPathSum()<=c){result.add(new ArrayList<>(path));return;}return;}//再加后面任意一个就肯定不够了if (getPathSum()<=c&&(getPathSum() + items_min_weight[startIndex]) > c) {//        if (getPathSum()<c) {result.add(new ArrayList<>(path));return;}for (int i = startIndex; i < n; i++) {path.add(i);backtracking(n,  i + 1);path.removeLast();}}public static int getPathSum() {int sum = 0;for (int i = 0; i < path.size(); i++) {sum += items_weight[path.get(i)];}return sum;}
}

八皇后问题

问题背景

八皇后问题是十九世纪著名的数学家高斯于1850年提出的。

• 问题是：在8×8的棋盘上摆放八个皇后， 使其不能互相攻击， 即任意两个皇后都不能处于同一行、 同一列或同一斜线上。

• n皇后问题：即在n× n的棋盘上摆放n个皇后， 使任意两个皇后都不能处于同一行、 同一列或同一斜线上。

搜索空间:N叉树

4后问题：解是一个4维向量， (x1, x2, x3, x4)（放置列号），这里x1为第一行，x2为第二行，以此类推。

搜索空间： 4叉树

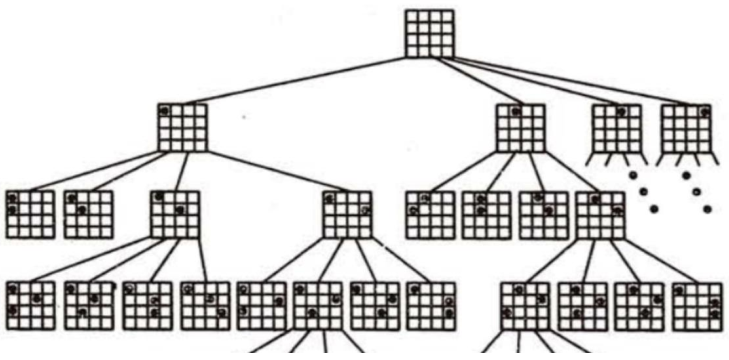
8后问题：解是一个8维向量， (x1, x2, x3, x4, x5, x6, x7, x8)

搜索空间： 8叉树,一个解： <1,3,5,2,4,6,8,7>

问题分析

确定问题状态： 问题的状态即棋盘的布局状态。

构造状态空间树： 状态空间树的根为空棋盘，每个布局的下一步可能布局是该布局结点的子结点。

由于可以预知，在每行中有且只有一个皇后，因此可采用逐行布局的方式，即每个布局有n个子结点

⚫ 设4个皇后为xi， 分别在第i行(i=1， 2， 3， 4)；

⚫ 问题的解状态：可以用(1, x1)， (2, x2)， ……， (4, x4)表示4个皇后的位置；

⚫ 由于行号固定， 可简单记为： (x1, x2, x3, x4)；例如：(4, 2, 1, 3)

⚫ 问题的解空间： (x1, x2, x3, x4)， 1≤xi≤4 (i=1， 2， 3， 4)， 共4! 个状态；

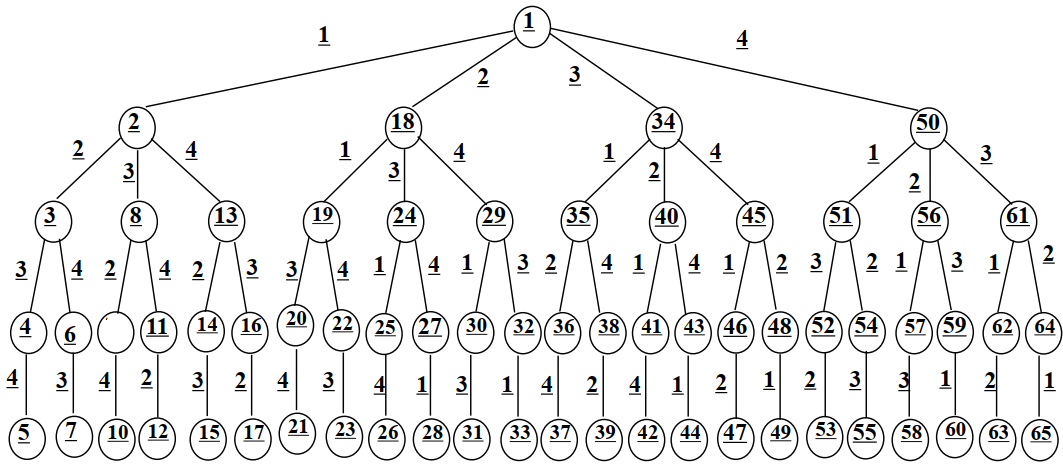
4皇后问题解空间的树结构

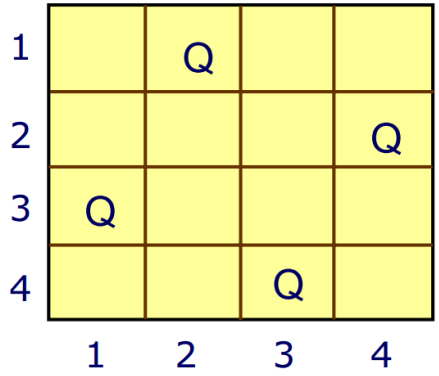
约束条件

⚫ 任意两个皇后不能位于同一行上;

⚫ 任意两个皇后不能位于同一列上，所以解向量X必须满足约束条件：

搜索解空间中进行剪枝

（1） 从空棋盘起， 逐行放置棋子。

（2） 每在一个布局中放下一个棋子， 即推演到一个新的布局。

（3） 如果当前行上没有可合法放置棋子的位置，则回溯到上一行， 重新布放上一行的棋子。

以4皇后问题为例

为了简化问题， 下面讨论4皇后问题。4皇后问题的解空间树是一个完全4叉树， 树的根结点表示搜索的初始状态， 从根结点到第2层结点对应皇后1在棋盘中第1行可能摆放的位置， 从第2层到第3层结点对应皇后2在棋盘中第2行的可能摆放的位置， 以此类推。

回溯法求解4皇后问题的搜索过程

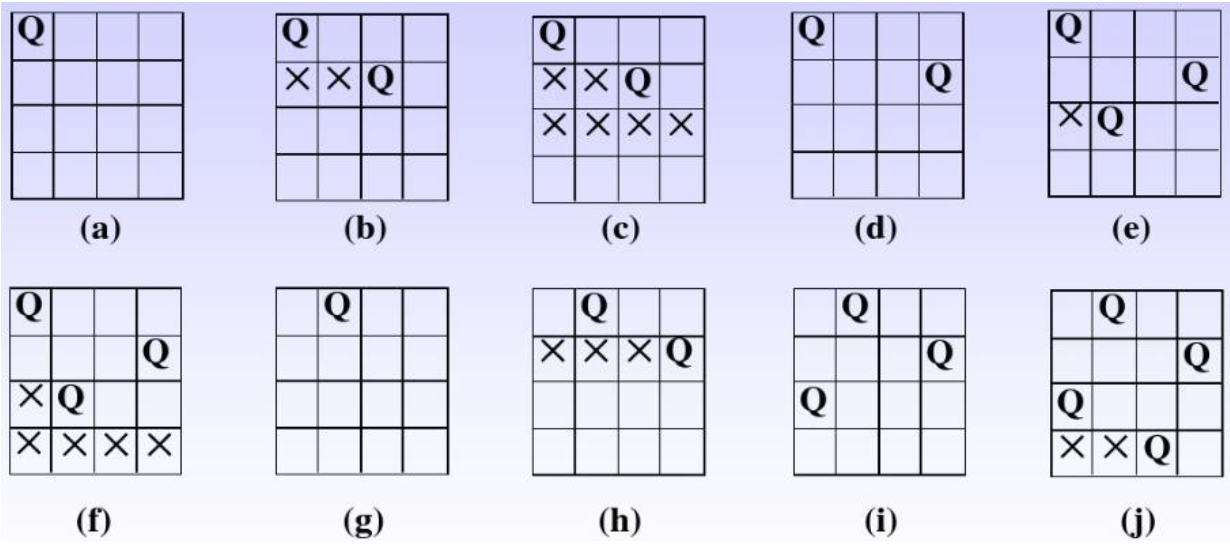
n=4的n皇后问题的搜索、 剪枝与回溯

代码思路

参考文章：代码随想录

回溯模板

void backtracking(参数) {if (终止条件) {存放结果;return;}for (选择：本层集合中元素（树中节点孩子的数量就是集合的大小）) {处理节点;backtracking(路径，选择列表); // 递归回溯，撤销处理结果}
}

递归终止条件

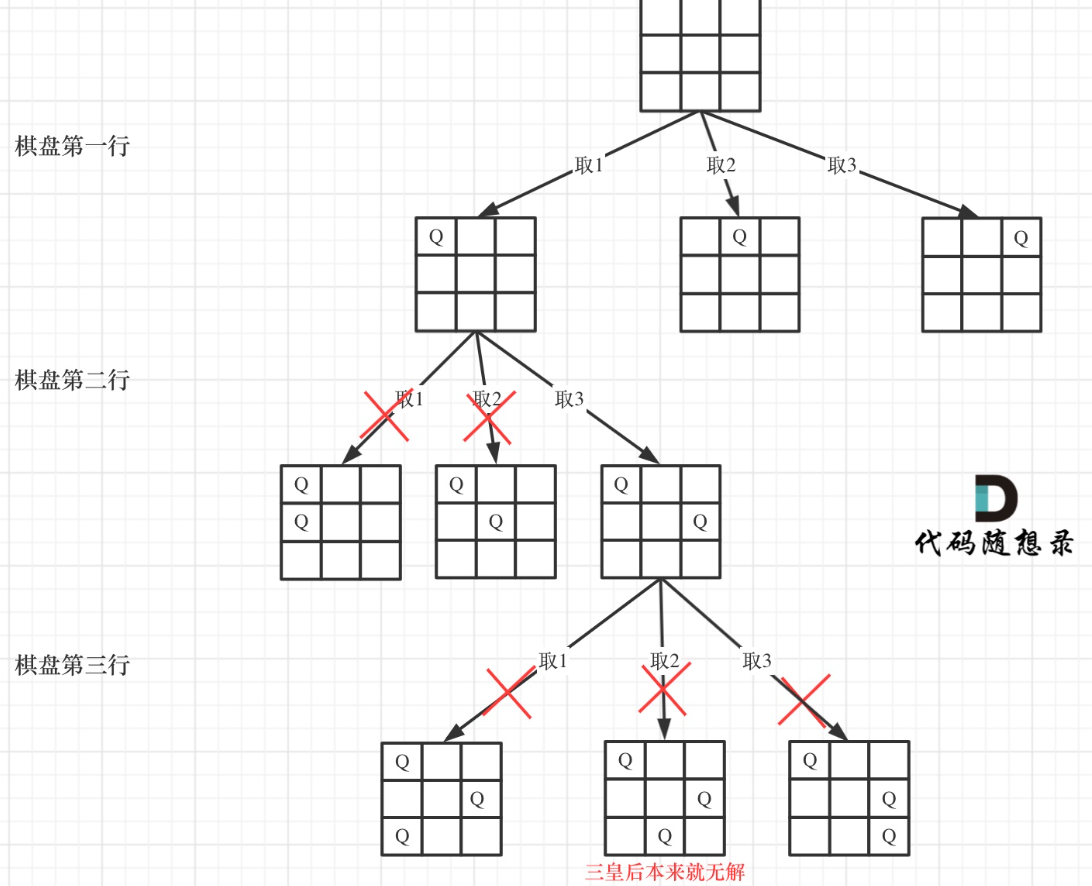
if (row == n) {result.push_back(chessboard);return;
}

单层搜索的逻辑

for (int col = 0; col < n; col++) {if (isValid(row, col, chessboard, n)) { // 验证合法就可以放chessboard[row][col] = 'Q'; // 放置皇后backtracking(n, row + 1, chessboard);chessboard[row][col] = '.'; // 回溯，撤销皇后}
}

验证棋盘是否合法

按照如下标准去重：

不能同行(搜索过程从上到下自动解决了这个问题)

不能同列

不能同斜线 （45度和135度角）

实现代码与相关解释

package DaiMaSuiXiangLu;import java.util.ArrayList;
import java.util.Arrays;
import java.util.List;public class N_queen {//res用来存储可能的结果static List<List<String>> res = new ArrayList<>();public static void main(String[] args) {int n = 4;//画棋盘n*nchar[][] chessboard = new char[n][n];for (char[] c : chessboard) {Arrays.fill(c, '.');}backTrack(n, 0, chessboard);for (int i = 0; i < res.size(); i++) {System.out.println("方案"+(i+1));for (int j = 0; j < res.get(i).size(); j++) {System.out.println(res.get(i).get(j));}}}/*** @param n          棋盘的大小* @param row        当初正在处理哪一行* @param chessboard 当前棋盘的状况*/public static void backTrack(int n, int row, char[][] chessboard) {if (row == n) {//将结果赋给的新的list//这是因为List是引用类型，需要每次开辟新的空间给一个新的list来保存结果res.add(Array2List(chessboard));return;}for (int col = 0; col < n; ++col) {//剪枝操作,暴力点也可以不剪枝，对最后保存下来的多个结果去检查他们的合法性//尝试对该行的每一列放置皇后if (isValid(row, col, n, chessboard)) {chessboard[row][col] = 'Q';backTrack(n, row + 1, chessboard);chessboard[row][col] = '.';}}}//用于生成新的listpublic static List Array2List(char[][] chessboard) {List<String> list = new ArrayList<>();for (char[] c : chessboard) {list.add(String.copyValueOf(c));}return list;}/**** @param row 当前递归是在row行,col列放置了一个新的皇后* @param col 当前递归是在row行,col列放置了一个新的皇后* @param n 棋盘大小* @param chessboard 当前棋盘的状况* @return 是否违背了合法性*/public static boolean isValid(int row, int col, int n, char[][] chessboard) {//行无需检查,因为backTrack的递归保证了每一行只有一个皇后// 检查列for (int i = 0; i < row; ++i) { // 相当于剪枝if (chessboard[i][col] == 'Q') {return false;}}// 检查45度对角线for (int i = row - 1, j = col - 1; i >= 0 && j >= 0; i--, j--) {if (chessboard[i][j] == 'Q') {return false;}}// 检查135度对角线for (int i = row - 1, j = col + 1; i >= 0 && j <= n - 1; i--, j++) {if (chessboard[i][j] == 'Q') {return false;}}return true;}}

暴力回溯法模版应用

组合问题

回到文章开头的问题

给定两个整数 n 和 k，返回 1 ... n 中所有可能的 k 个数的组合。

示例: 输入: n = 4, k = 2 输出: [ [2,4], [3,4], [2,3], [1,2], [1,3], [1,4]]

添加的solveCombinationProblem仅仅是用来筛选满足条件的解

package DaiMaSuiXiangLu;import java.util.ArrayList;
import java.util.LinkedList;
import java.util.List;public class KnapsackProblem1 {static List<List<Integer>> result = new ArrayList<>();//path记录所有的可能,最后结果总共个数必定为2^Nstatic LinkedList<Integer> path = new LinkedList<>();//N代表着问题规模的大小,即2^N,最终的叶子结点个数就是2^Nstatic int N = 4;public static void main(String[] args) {//组合问题int K = 2;solveCombinationProblem(K);}public static void backtracking() {if (path.size() == N) {//找到了一个叶子结点，就保存下来//就算这个叶子结点是不满足题目的要求也保存下来result.add(new ArrayList<>(path));return;}path.add(1);backtracking();path.removeLast();path.add(0);backtracking();path.removeLast();}public static void solveCombinationProblem(int k) {int time = 0;for (int i = 0; i < result.size(); i++) {//用来记录该叶子结点中1的个数time = 0;List<Integer> answer = result.get(i);for (int j = 0; j < answer.size(); j++) {if (answer.get(j) == 1) {time++;}}if (time == k) {for (int j = 0; j < answer.size(); j++) {if (answer.get(j) == 1) System.out.print((j + 1) + " ");}System.out.println();}}}
}

0-1背包问题 

用之前回溯法的模版会发现终止条件不好写出来

回溯法:0-1背包问题-CSDN博客

但用该文章推荐的模版很好地解决这个问题

import java.util.ArrayList;
import java.util.LinkedList;
import java.util.List;public class KnapsackProblem1 {static List<List<Integer>> result = new ArrayList<>();//path记录所有的可能,最后结果总共个数必定为2^Nstatic LinkedList<Integer> path = new LinkedList<>();//N代表着问题规模的大小,即2^N,最终的叶子结点个数就是2^Nstatic int N = 4;public static void main(String[] args) {backtracking();//背包问题int[] items_weight={8,6,4,3};int[] items_value={12,11,9,8};int C=13;solveKnapsackProblem(items_weight,items_value,C);}public static void backtracking() {if (path.size() == N) {//找到了一个叶子结点，就保存下来//就算这个叶子结点是不满足题目的要求也保存下来result.add(new ArrayList<>(path));return;}path.add(1);backtracking();path.removeLast();path.add(0);backtracking();path.removeLast();}public static void solveKnapsackProblem(int[] items_weight, int[] items_value, int C) {//值得注意的是items_weight和items_value的长度都为Nint sum_weight = 0;int sum_value = 0;//记录现在能达到的最大价值int max_value = -1;for (int i = 0; i < result.size(); i++) {sum_weight = 0;sum_value = 0;List<Integer> answer = result.get(i);for (int j = 0; j < answer.size(); j++) {if (answer.get(j) == 1) {sum_value += items_value[j];sum_weight += items_weight[j];}}//不高于背包容量且比之前找到的最大价值还大if (sum_weight <= C && sum_value > max_value) {max_value = sum_value;}}System.out.println(max_value);}
}