有 N
组物品和一个容量是 V
的背包。

每组物品有若干个，同一组内的物品最多只能选一个。
每件物品的体积是 vij
，价值是 wij
，其中 i
是组号，j
是组内编号。

求解将哪些物品装入背包，可使物品总体积不超过背包容量，且总价值最大。

输出最大价值。

输入格式
第一行有两个整数 N，V
，用空格隔开，分别表示物品组数和背包容量。

接下来有 N
组数据：

每组数据第一行有一个整数 Si
，表示第 i
个物品组的物品数量；
每组数据接下来有 Si
行，每行有两个整数 vij,wij
，用空格隔开，分别表示第 i
个物品组的第 j
个物品的体积和价值；
输出格式
输出一个整数，表示最大价值。

数据范围
0<N,V≤100

0<Si≤100

0<vij,wij≤100
输入样例
3 5
2
1 2
2 4
1
3 4
1
4 5
输出样例：
8

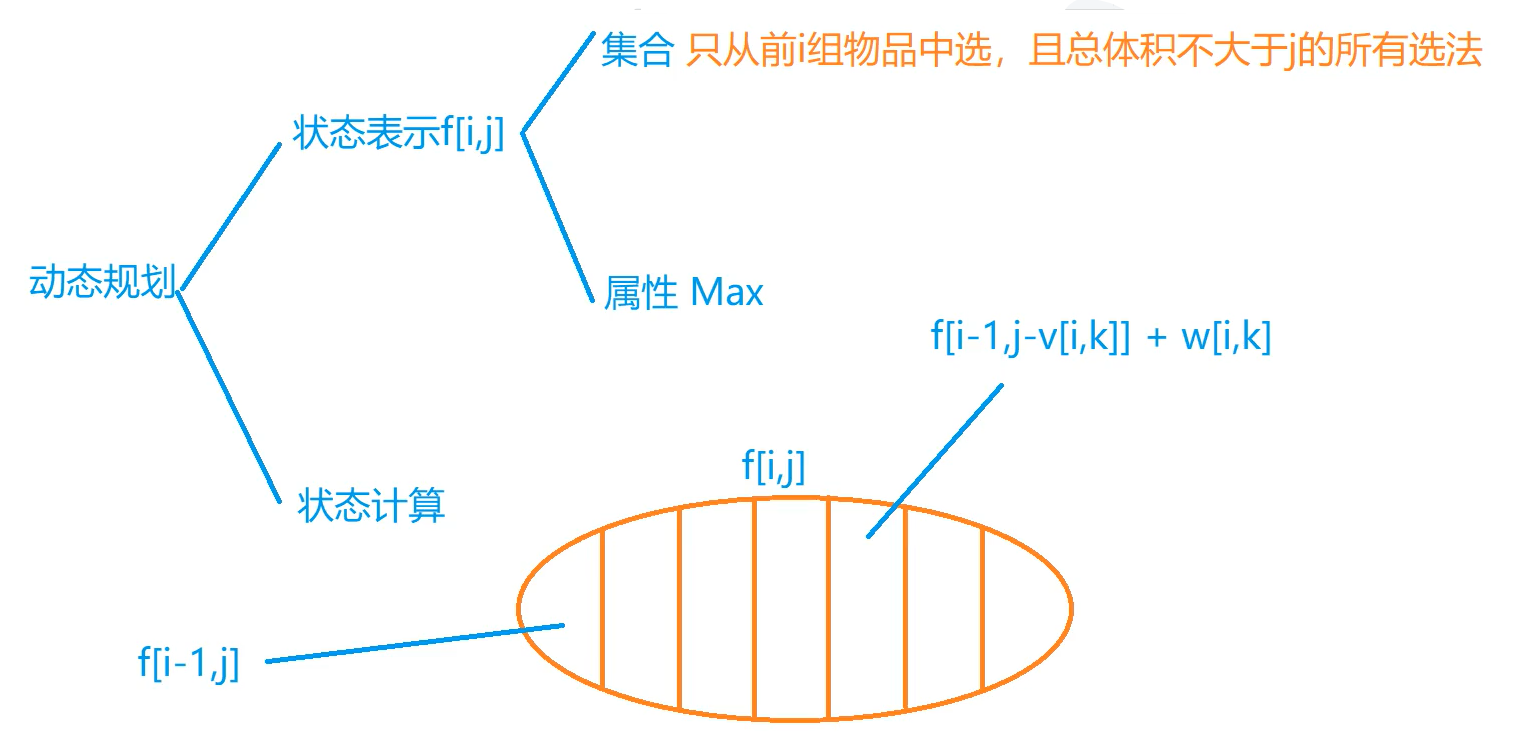
动态规划中，状态转移时候如果用到的是上一层的状态的话，就从大到小来枚举体积（保证算体积的时候，所用到的体积还没有被用过），如果用到的是本层的状态的话，就从小到大来枚举体积。

#include <iostream>
#include <algorithm>using namespace std;const int N = 110;
int n, m;
int v[N][N], w[N][N], s[N];
int f[N];int main ()
{cin>>n>>m;for(int i = 1; i <= n; i ++ ){cin>>s[i];for(int j = 0; j < s[i]; j ++ )cin>>v[i][j]>>w[i][j];}for(int i = 1; i <= n; i ++ )for(int j = m; j >= 0; j -- ) //从大到小枚举所有体积for(int k = 0; k < s[i]; k ++ )if(v[i][k] <= j) //条件为真才有更新的必要f[j] = max(f[j], f[j - v[i][k]] + w[i][k]);cout<<f[m]<<endl;return 0;
}