师从清风
矩阵的创建方法
在MATLAB中,矩阵的创建方法主要有三种,分别是:直接输入法、函数创建法和导入本地文件中的数据。
直接输入法
输入矩阵时要以中括号“[ ]”作为标识符号,矩阵的所有元素必须都在中括号内。
矩阵的同行元素之间用空格或逗号分隔,行与行之间用分号或回车键分隔。
a = [1 2 3; 4 5 6]
b = [1,2,3; 4,5,6]
c = [2 56 7]
d = [3 6;6 9] % 还可以既加分号又加回车键进行换行如果不想显示输出结果,可以在语句的最后用英文分号“;”结束。(工作区还是可以找到我们创建的矩阵)
e = [2, 35, 7];函数创建法
MATLAB提供了一些函数,这些函数可以用来生成某些特定的矩阵,我们这里介绍几个最常用到的函数。
zeros、ones和eye
这三个函数可用来分别创建全为0的矩阵、全为1的矩阵和单位矩阵。
以zeros函数为例,其常见的用法有两种:
(1)zeros(n)可以创建一个n行n列全为0的矩阵;
(2)zeros(m,n)可以创建一个m行n列全为0的矩阵。
a = zeros(3) b = zeros(2,3) c = ones(5) d = ones(1,4)
单位矩阵:主对角线元素为 1 且其他位置元素为 0 。
e = eye(4)
f = eye(4,3)
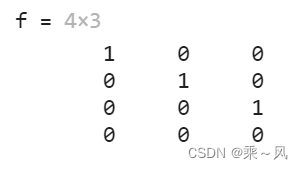
g = eye(3,4)

rand、randi和randn
这三个函数分别用来创建均匀分布的随机数、均匀分布的随机整数和标准正态分布的随机数
rand函数可用来创建区间0到1均匀分布的随机数,其最常用的方法有两种:
(1)rand(n)可以创建一个n行n列的随机数矩阵;
(2)rand(m,n)可以创建一个m行n列的随机数矩阵。
由rand函数创建的随机数矩阵的每个元素都随机取样自0和1之间的均匀分布。
rand(3) rand(3,2)
randi函数是用来创建均匀分布的随机整数(randi后的i是integer的缩写),其最一般的使用方法为:randi([imin,imax],m,n),可以用来创建一个m行n列的随机数矩阵,该随机数矩阵中的每个元素都是从区间[imin,imax]内随机抽取的整数。
例子:假设我们要模拟投掷100次骰子,骰子有6个面,那么我们可以使用randi([1,6],1,100)得到一个长度为100的行向量,向量中的每个元素都是取自1,2,3,4,5,6中的一个整数。
randi([1,6],1,100) % 这里我生成一个行向量,也可以生成列向量
另外,如果imin等于1,那么可以简写为randi(imax,m,n);
randi(6,1,100)
如果m和n相同,即生成一个n行n列的方阵,那么可以直接写成randi([imin,imax],n)。
randi([-3 3],5)
randn函数用来创建标准正态分布的随机数(randn后的n是norm distribution的缩写),其使用方法和rand函数类似:
(1)randn(n)可以创建一个n行n列的随机数矩阵;
(2)randn(m,n)可以创建一个m行n列的随机数矩阵。
注:1、由randn函数创建的随机数矩阵的每个元素都随机取样自标准正态分布。
2、标准正态分布:以0为均值、以1为标准差的正态分布,记为N(0,1).
diag和blkdiag
diag函数可用来创建对角矩阵或者获取矩阵的对角元素(diagonal 对角的)。
情况1:如果输入的第一个参数是向量,则表示创建对角矩阵。
diag(v,k) 将向量v的元素放置在第k条对角线上,其他位置元素为0。
k=0 表示主对角线,k>0 位于主对角线上方,k<0 位于主对角线下方。
如果k=0, 可以直接写成diag(v)。
diag([1,2,3]) % 或者写成diag([1,2,3], 0)
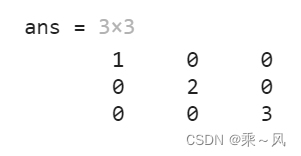
diag([1,2,3],-1)
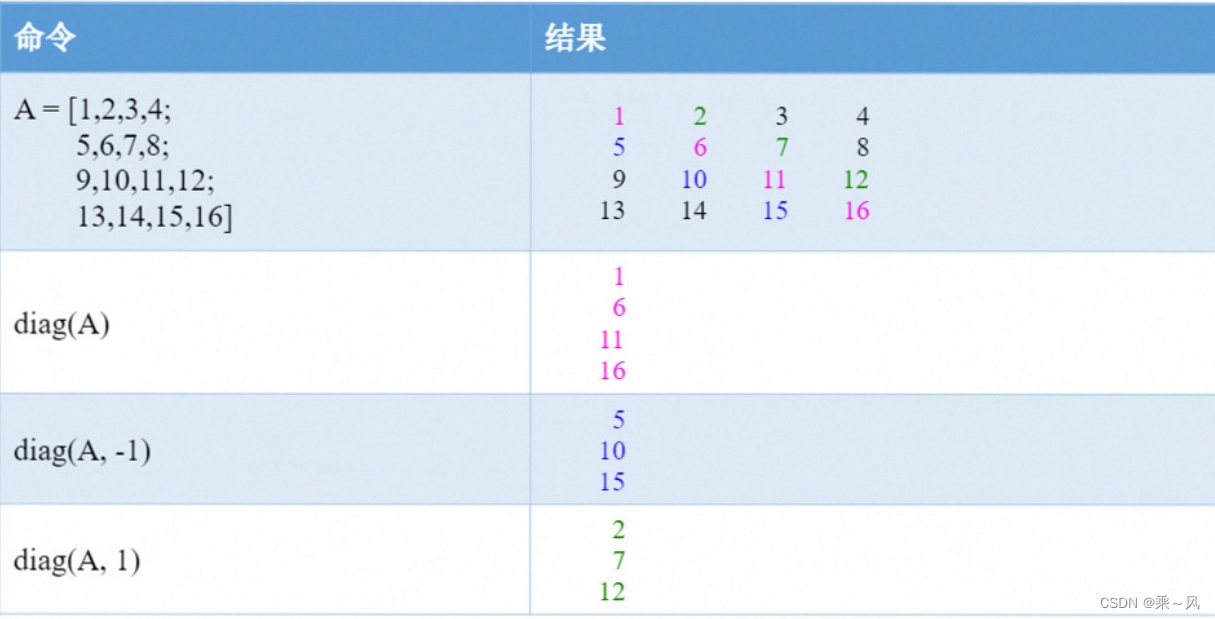
情况2:如果输入的第一个参数是矩阵,则表示获取矩阵的对角元素。
diag(A,k) 返回A的第k条对角线上元素的构成的列向量。
k表示对角线编号,我们将其指定为一个整数。
k=0 表示主对角线,k>0 位于主对角线上方,k<0 位于主对角线下方。
如果k=0, diag(A, 0)可以直接写成diag(A)。
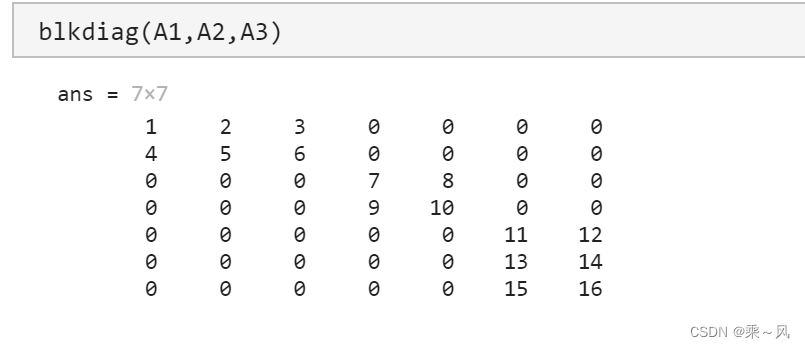
blkdiag函数可用来创建分块对角矩阵(block diagnoal 分块对角)。
分块对角矩阵是相对于常规的对角矩阵而言的,常规的对角矩阵沿对角线具有单个元素,而分块对角矩阵的对角线的元素是矩阵。
我们可采用以下形式表示一个分块对角矩阵:
A1 = [1,2,3;4,5,6]
A2 = [7,8;9,10]
A3 = [11,12;13,14;15,16]
blkdiag(A1,A2,A3)
导入本地文件中的数据
MATLAB可读取本地的文件,支持的常见格式如下:
.txt、.dat 或 .csv(适用于带分隔符的文本文件)
.xls、.xlsb、.xlsm、.xlsx、.xltm、.xltx 或 .ods(适用于电子表格文件)
矩阵元素的引用
双下标索引
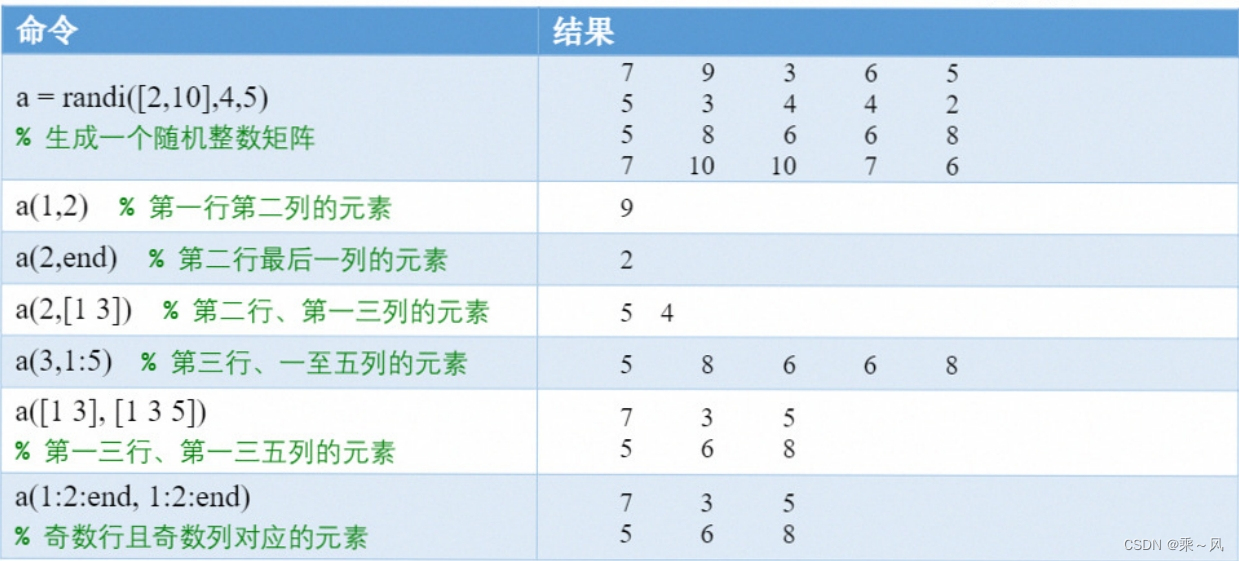
我们可以使用矩阵元素所处的行(row)和列(column)来进行引用矩阵的某一个元素,方式为:a(row_ind, column_ind).
size函数
可以使用size函数来计算矩阵的大小
有三种常见的用法:
(1)size(A) 返回一个行向量,其元素是 A 的相应维度的长度。
A = ones(4,6) % 全为1的矩阵
s = size(A) % 返回[4,6],表示有4行和6列

(2)size(A,dim)返回在维度dim上的长度。dim=1表示行;dim=2表示列
r_num = size(A,1) % 行数 r_num=4
c_num = size(A,2) % 列数 c_num=6
注意:即使A是一个向量,size(A)返回的结果也是一个向量,而不是向量的长度。
A = 1:5; % 行向量:[1 2 3 4 5]
size(A)=1 5
(3)size函数可以有两个返回值
第一个返回的元素用来保存行数;第二个返回的元素用来保存列数
A = zeros(3,5)
[r, c] = size(A) %输出 r=3 c=5
length函数和numel函数也可以用在矩阵上。
length函数会返回行和列的较大值
A = ones(3,4)
length(A)=4
numel函数会返回矩阵中元素的总数
numel(A)=3*4=12
有时候我们需要取出矩阵的某一行或者某一列。以取出矩阵A的第一行为例,我们可以使用代码A(1, 1:end),即row_ind取1表示第一行,column_ind取1:end表示从1到最后一列的索引。
A = randi([2,10],4,5)
A(1,1:end)
这时候我们可以直接将其简写为:A(1, :),逗号后面是列索引的位置,加一个冒号就表示取出每一列的元素。
A(1,:)
同理,要取第一列的所有元素,我们可以使用代码:A(:, 1)
A(:, 1)
总结:
A(:, n) 表示矩阵A的第n列的所有元素。
A(m, :) 表示矩阵A的第m行的所有元素。
线性索引(单下标)
使用单个下标对矩阵进行索引这种单下标的索引方法称为线性索引。
事实上,在MATLAB中,矩阵的数据在计算机的内存中被存储为单列。以下图为例,下面的矩阵虽然显示为 3×3 矩阵,但MATLAB在内存中将它存储为单列,由它的各列顺次连接而成。
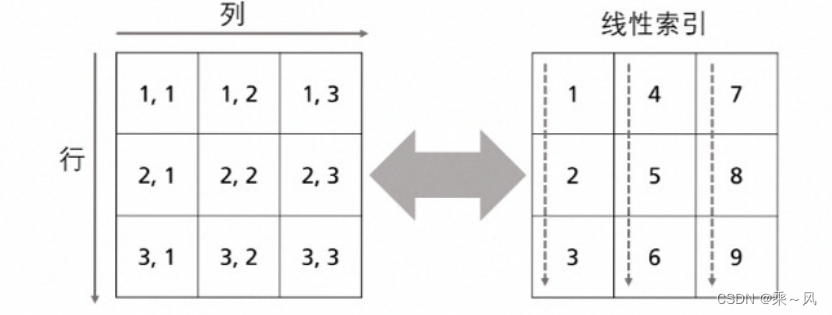
我们可以利用线性索引来取出矩阵中的元素,尽管这种方式并不那么直观。
举个例子:
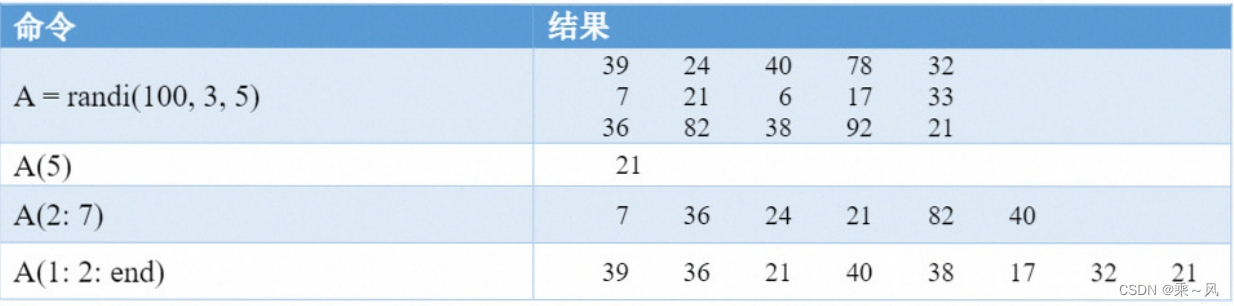
A(:)命令可以将A中的所有元素按照线性索引的方式重构成一个列向量,这个命令后面会经常用到。
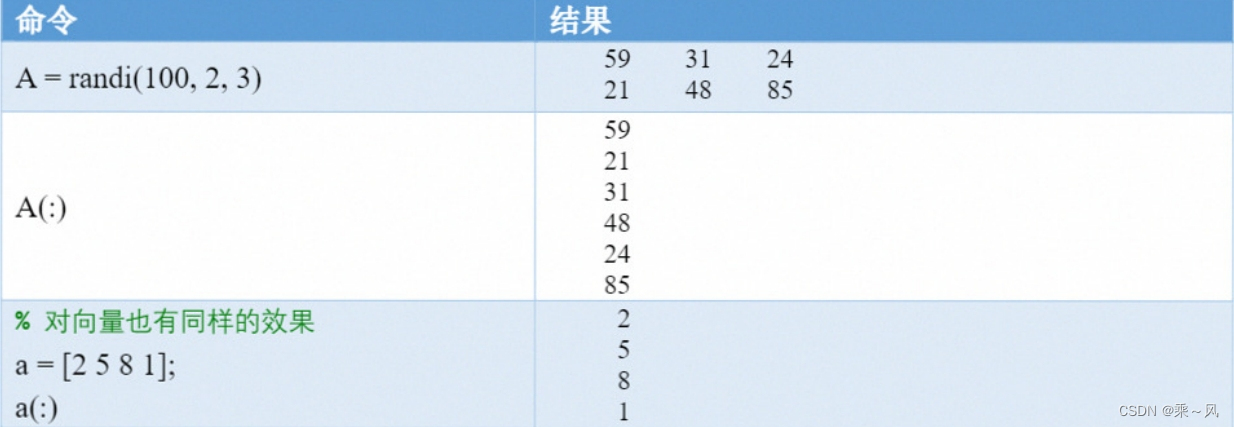
sub2ind和ind2sub函数
可用于在矩阵的原始索引(双下标)和线性索引之间进行转换(用到频率不高)(subscript 下标)。
sub2ind将矩阵的下标转换为线性索引
ind = sub2ind(sz,row,col) 针对大小为 sz 的矩阵返回由 row 和 col 指定的行列下标的对应线性索引 ind。此处,sz 是包含两个元素的向量,其中 sz(1) 指定行数,sz(2) 指定列数。
ind2sub将线性索引转换为下标[row,col] = ind2sub(sz,ind) 返回数组 row 和 col,其中包含与大小为 sz 的矩阵的线性索引 ind 对应的等效行和列下标。此处,sz 是包含两个元素的向量,其中 sz(1) 指定行数,sz(2) 指定列数。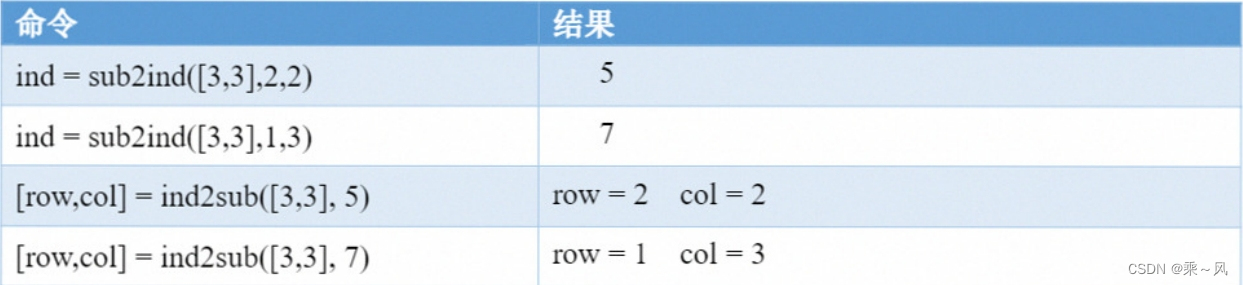
矩阵元素的修改和删除
1、可以直接利用等号赋值的方法对引用位置的元素进行修改,用法和对向量元素的修改类似。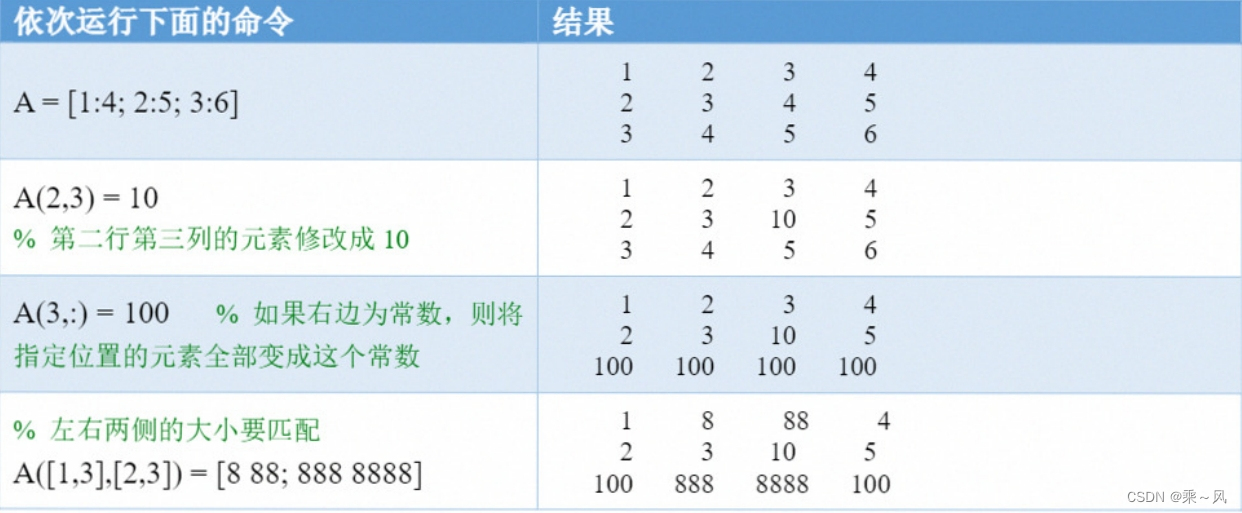
2、可以使用线性索引(单下标的索引)的方式对矩阵的元素进行修改: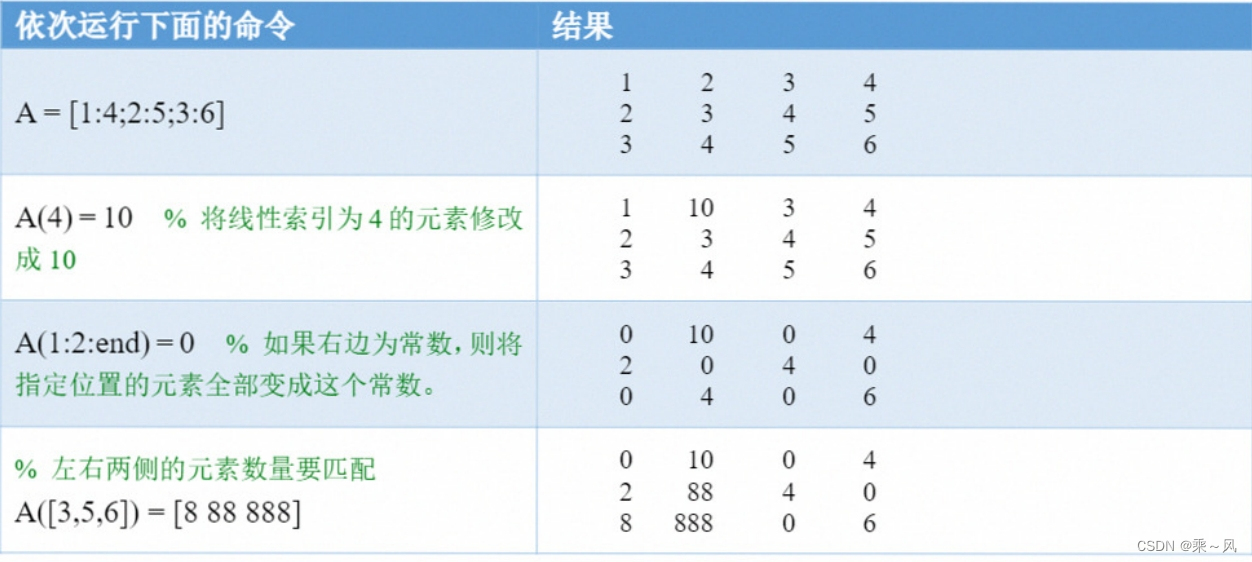
3、对矩阵进行拓展
通过将一个或多个元素置于矩阵现有的行和列索引边界之外,可以将它们添加到矩阵中。MATLAB 会自动用 0 填充矩阵,使其保持为矩形。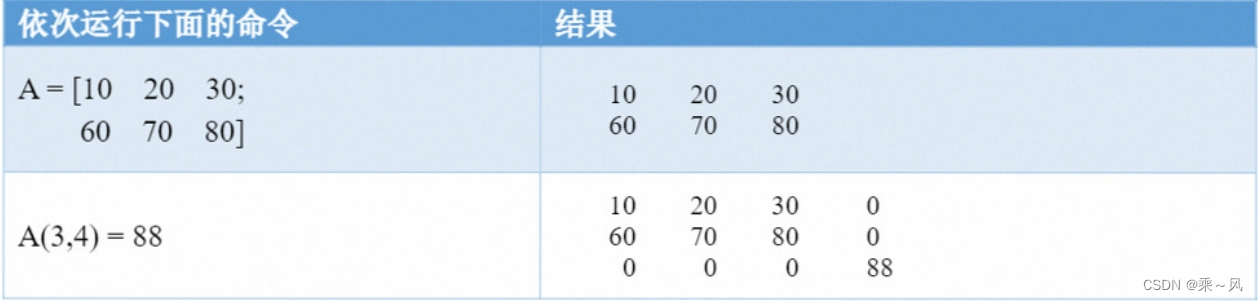
还可以通过在现有索引范围之外插入新矩阵来扩展其大小。
如果我们将等号右侧变成空向量[ ],则可以删除对应位置的元素。需要注意的是,通常只能删除矩阵的整行或者整列,否则会报错。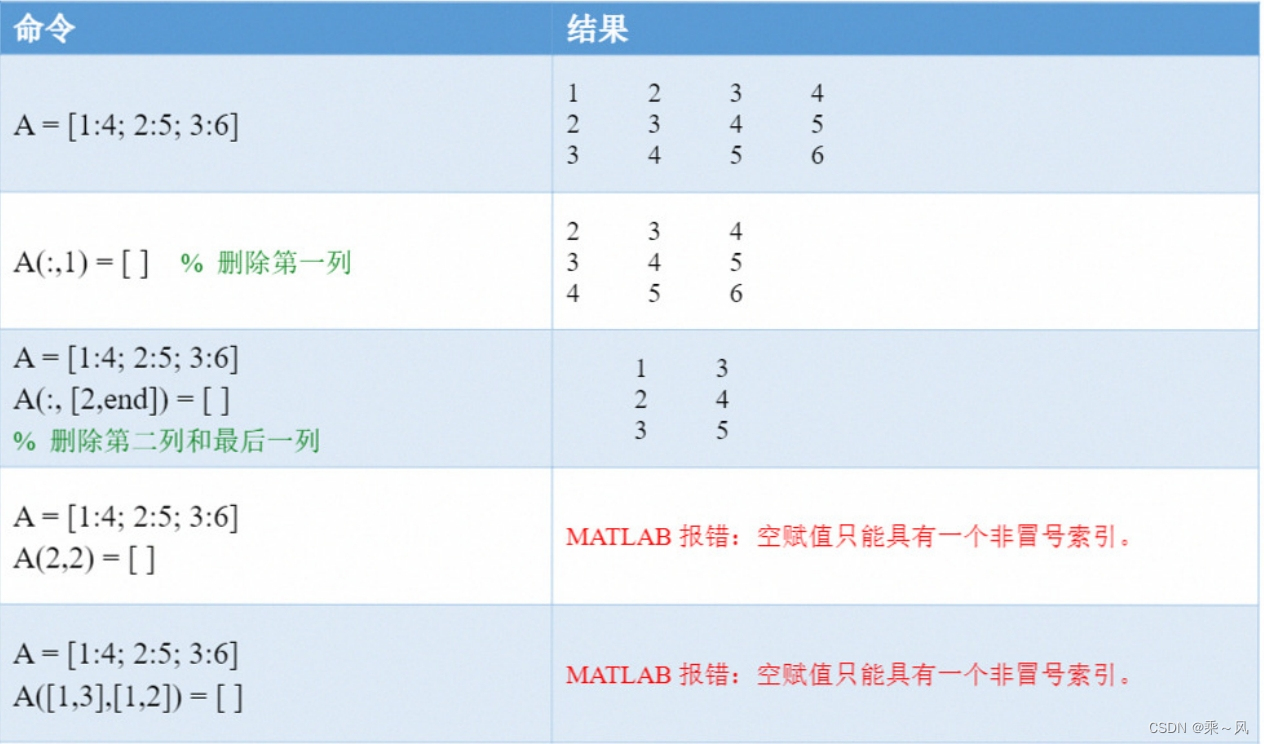
注意,也可以通过线性索引来删除矩阵的元素。使用线性索引删除后,MATLAB会将矩阵中剩下的元素按照线性索引的顺序放入到一个向量中。另外,使用线性索引可以删除任意位置的元素,不需要删除矩阵的一整行或者一整列。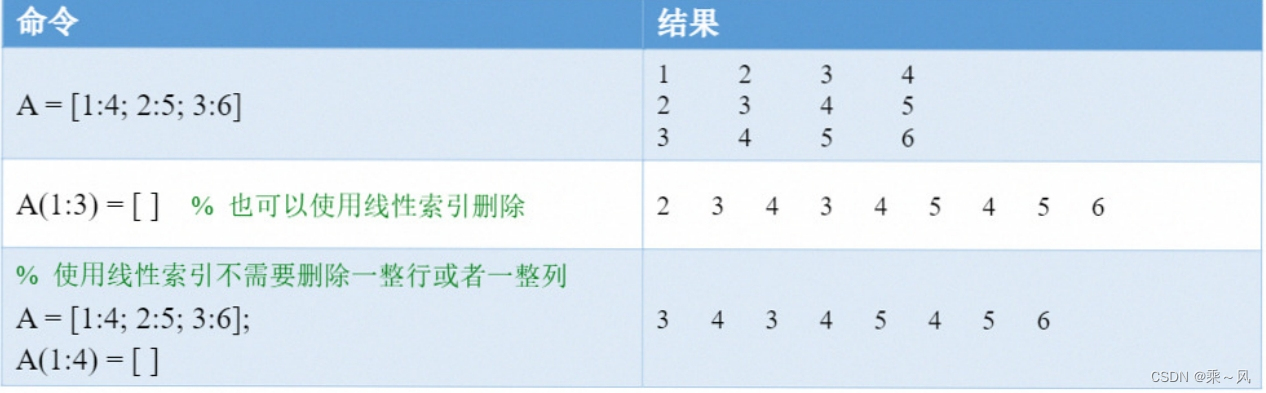
矩阵的拼接和重复
矩阵的拼接
有时候我们需要对多个矩阵进行拼接,变成一个大的矩阵。
根据矩阵拼接的方向,我们可以分为横向(水平)拼接和纵向(垂直)拼接,如下图所示:
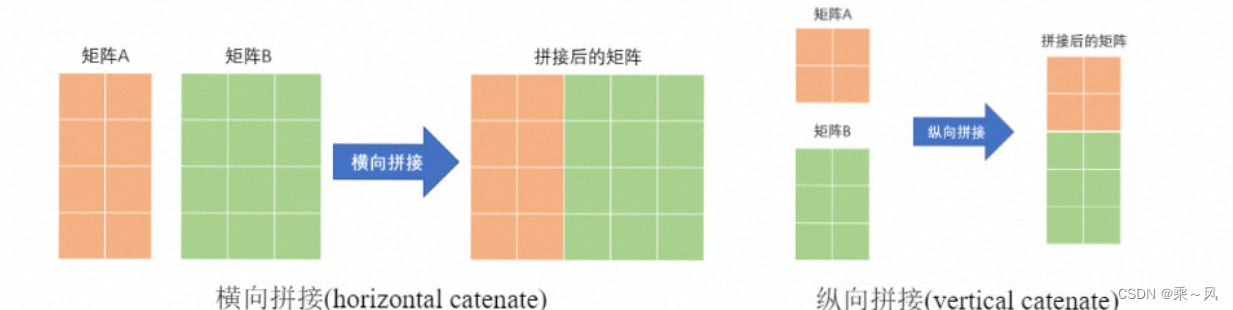
如上图所示:横向拼接要求矩阵的行数相同;纵向拼接要求矩阵的列数相同。
在MATLAB中,我们可以使用命令[A, B] 或 [A B]对矩阵A和B进行横向拼接,也可以使用MATLAB中的内置函数:horzcat(A,B);
A = [1 6 7; 4 5 7]
B = [3 1; 5 10]
[A, B]
[A B] % 用空格隔开,可以有多个空格
horzcat(A,B)
cat(2,A,B)
类似的,我们可以使用命令[A; B]对矩阵A和B进行纵向拼接,也可以使用MATLAB中的内置函数:vertcat(A,B)。
A = [2 4 5;2 2 4]
B = [1 8 6;6 3 10;1 5 5]
[A; B]
[A
B] % 也可以使用回车键进行纵向拼接
vertcat(A,B)
cat(1,A,B)
下面是cat函数的帮助链接:
https://ww2.mathworks.cn/help/matlab/ref/double.cat.html
命令cat(dim,A,B)表示沿维度 dim 方向将矩阵B拼接到矩阵A的末尾。
dim = 1时表示从上自下沿着行方向拼接,即纵向拼接,因此cat(1,A,B)等价于vertcat(A,B);
dim = 2时表示从左自右沿着列方向拼接,即横向拼接,因此cat(2,A,B)等价于horzcat(A,B)。
大小不匹配会报错
矩阵的重复
有时候我们需要对同一个矩阵进行重复的堆叠。
例如将矩阵A的内容堆叠在m行n列的新矩阵中,这个新矩阵每一行由n个A组成,每一列由m个A组成。
下面我们画一个示意图:
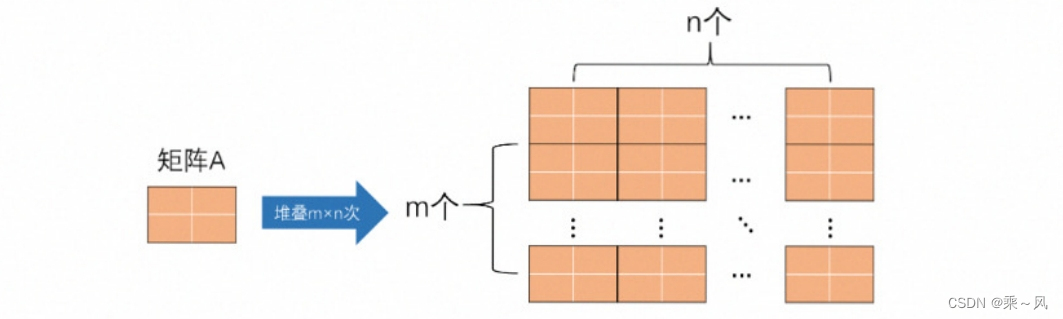
在MATLAB中,对同一个矩阵进行重复的堆叠的代码为repmat(A,m,n)。
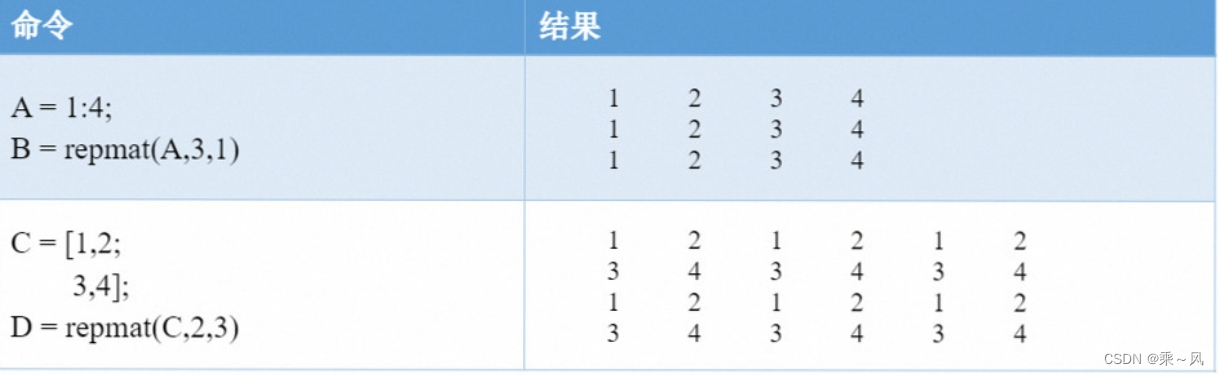
对向量或者矩阵中的元素进行重复,使用到的函数是repelem。(使用较少)
情况1:重复向量v中的元素:repelem(v,n)
当n为一个正整数时,表示把向量v中的每一个元素都重复n次;
n也可以为一个向量,其长度必须和v的长度相同,它可以将v的每个元素指定重复n对应元素的次数。
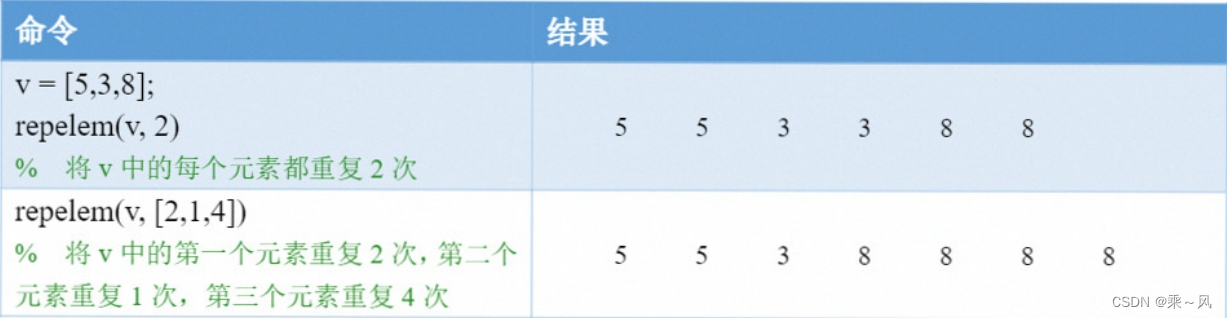
情况2:重复矩阵A中的元素:repelem(A,m,n)
m和n分别表示沿着行方向(从上至下)和列方向(从左至右)将矩阵元素重复的次数,这里的m和n可以是正整数,也可以是向量。
如果m是向量,则m的长度要和矩阵A的行数相同;如果n是向量,则n的长度要和矩阵A的列数相同。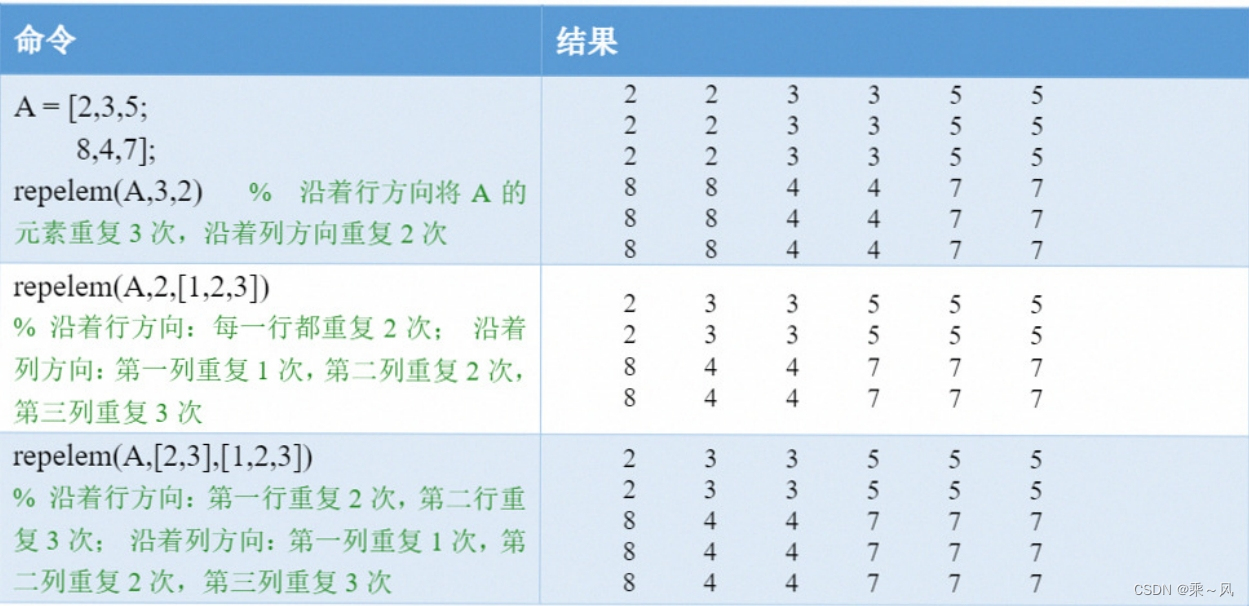
若有侵权,请联系作者
![P1967 [NOIP2013 提高组] 货车运输](http://pic.xiahunao.cn/P1967 [NOIP2013 提高组] 货车运输)








)








 写一个属于自己的 ChatGPT 新版 WebUI)
