目录
1.浮点数是什么？
2. 浮点数存储规则
1.浮点数是什么？
就是数学中的小数。
常见的浮点数：
3.14159
1E10（1*10^10）
浮点数家族包括： float、double、long double 类型。
浮点数表示的范围：float.h中定义(图1-1,图1-2)
图1-1
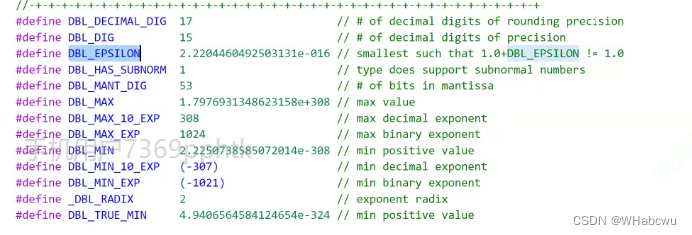
图1-2
2. 浮点数存储规则
根据国际标准 IEEE （电气和电子工程协会） 754 ，任意一个二进制浮点数 V 可以表示成下面的形式：
(-1)^S * M * 2^E(-1)^S 表示符号位，当 S=0 ， V 为正数；当 S=1 ， V 为负数。M 表示有效数字，大于等于 1 ，小于 2。2^E 表示指数位。
举例：5.5表示 一个二进制浮点数
小数点前的5- >二进制:101
小数点后的5- >二进制:1
写作：101.1
为啥呢？（图解2-1）
图解2-1
将其用科学计数法表示:1.011*2^2
S=0 M=1.011 E=2
故：(-1)^0*1.011*2^2
浮点型在内存中的存储图
IEEE 754 规定：
（1）对于 32 位的浮点数，（图2-2）最高的 1 位是符号位 S ，接着的 8 位是指数 E ，剩下的 23 位为有效数字 M 。
图2-2
（2）对于 64位的浮点数，（图2-3）最高的1 位是符号位S，接着的 11 位是指数 E ，剩下的 52 位为有效数字 M 。
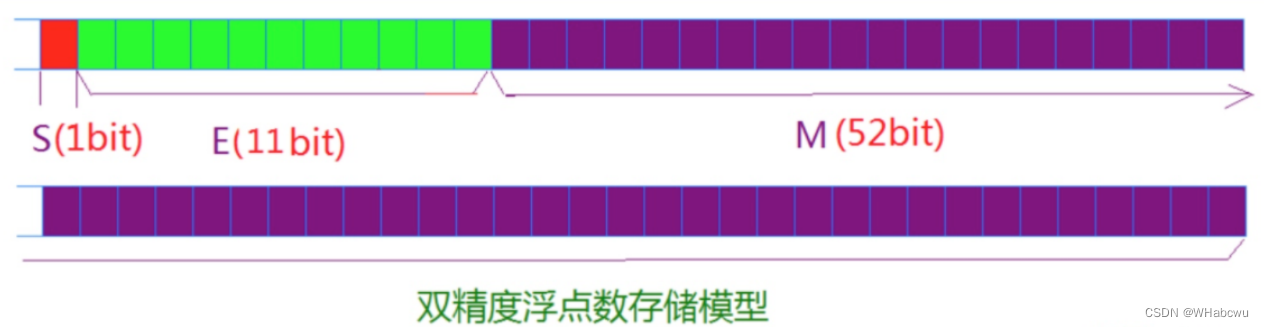
S无非存的是0/1。
但对有效数字M和指数E，还有一些特别规定。
1.M
前面说过， 1≤M<2 ，也就是说， M 可以写成 1.xxxxxx 的形式，其中 xxxxxx 表示小数部分。
在计算机内部保存 M 时， 默认这个数的第一位总是1，因此可以被舍去，只保存后面的
xxxxxx部分。
比如保存 1.01 的时候
只保存01 ， 等到读取的时候，再把第一位的1加上去。
这样做的目的，是节省1位有效数字。 以 32 位 浮点数为例，留给M 只有 23 位， 将第一位的1 舍去以后，等于可以保存 24 位有效数字。
2.E
首先， E 为一个无符号整数（ unsigned int ）
这意味着，如果 E 为 8 位，它的取值范围为 0~255 ；如果 E 为 11 位，它的取值范围为 0~2047 。但是，我们 知道，科学计数法中的E 是可以出 现负数的，所以IEEE 754 规定， 存入内存时E的真实值必须再加上一个中间数，对于8位的E，这个中间数 是127；对于11位的E，这个中间 数是1023。
举例：0.5
二进制形式为0.1，由于规定正数部分必须为1，即将小数点右移1位，则为 1.0*2^(-1)，
其阶码E为-1+127=126，表示为 01111110，
尾数M为1.0去掉整数部分为0，补齐0到23位00000000000000000000000
则其二进 制表示形式为:
0 01111110 00000000000000000000000
E全为0
这时，浮点数的指数 E 等于 1-127 （或者 1-1023 ）即为真实值，
有效数字M不再加上第一位的1，而是还原为0.xxxxxx的小数。 这样做是为了表示 ±0 ，以及接近于
0 的很小的数字。
E 全为 1
如果有效数字M全为0，表示±无穷大（正负取决于符号位s）。
以上为我个人的小分享，如有问题，欢迎讨论！！！
![[驱动开发]字符设备驱动应用——点灯](https://img-blog.csdnimg.cn/a0ef0b3f46424f258ec4d32e0324a17a.png)
