654. 最大二叉树
给定一个不重复的整数数组 nums 。 最大二叉树 可以用下面的算法从 nums 递归地构建:
- 创建一个根节点,其值为
nums中的最大值。 - 递归地在最大值 左边 的 子数组前缀上 构建左子树。
- 递归地在最大值 右边 的 子数组后缀上 构建右子树。
返回 nums 构建的 最大二叉树 。
示例 1:
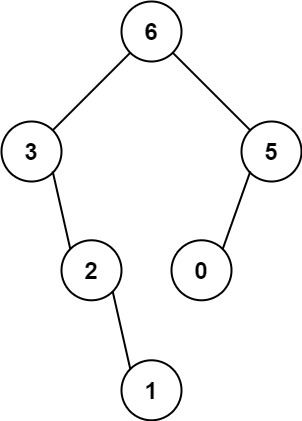
输入:nums = [3,2,1,6,0,5] 输出:[6,3,5,null,2,0,null,null,1] 解释:递归调用如下所示: - [3,2,1,6,0,5] 中的最大值是 6 ,左边部分是 [3,2,1] ,右边部分是 [0,5] 。- [3,2,1] 中的最大值是 3 ,左边部分是 [] ,右边部分是 [2,1] 。- 空数组,无子节点。- [2,1] 中的最大值是 2 ,左边部分是 [] ,右边部分是 [1] 。- 空数组,无子节点。- 只有一个元素,所以子节点是一个值为 1 的节点。- [0,5] 中的最大值是 5 ,左边部分是 [0] ,右边部分是 [] 。- 只有一个元素,所以子节点是一个值为 0 的节点。- 空数组,无子节点。
示例 2:
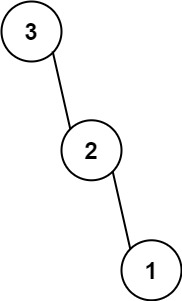
输入:nums = [3,2,1] 输出:[3,null,2,null,1]
思路:要找最大值来创建二叉树,考虑到可能会用到迭代,通过遍历来找到最大结点在数组中的下标,对左右孩子结点进行同样的操作,所以会需要到一个用于迭代的函数,参数中需要包括到范围(以确定左右子树所包含的元素在数组中的位置)。
代码实现:
class Solution {
public:TreeNode *generate(const vector<int>& nums, int begin, int end) {if(begin >= end) return nullptr;int maxNumIdx = begin;for (int i = begin; i < end; ++i) {if (nums[i] > nums[maxNumIdx]) maxNumIdx = i;}TreeNode *root = new TreeNode(nums[maxNumIdx]);root->left = generate(nums, begin, maxNumIdx);root->right = generate(nums, maxNumIdx + 1, end);return root;}TreeNode* constructMaximumBinaryTree(vector<int>& nums) {return generate(nums, 0, nums.size());}
};617.合并二叉树
给你两棵二叉树: root1 和 root2 。
想象一下,当你将其中一棵覆盖到另一棵之上时,两棵树上的一些节点将会重叠(而另一些不会)。你需要将这两棵树合并成一棵新二叉树。合并的规则是:如果两个节点重叠,那么将这两个节点的值相加作为合并后节点的新值;否则,不为 null 的节点将直接作为新二叉树的节点。
返回合并后的二叉树。
注意: 合并过程必须从两个树的根节点开始。
示例 1:
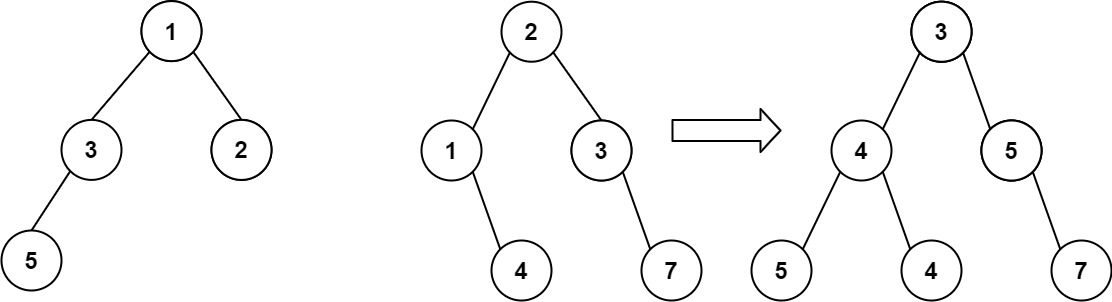
输入:root1 = [1,3,2,5], root2 = [2,1,3,null,4,null,7] 输出:[3,4,5,5,4,null,7]
示例 2:
输入:root1 = [1], root2 = [1,2] 输出:[2,2]
思路:在之前判定一颗二叉树是否对称时,我们使用到了队列(判断一棵树的左右子树),而此处,同样可以使用一个队列来对对应的结点进行处理。用到迭代的方法,修改第一棵树,而不是重新创建一棵树。
代码实现:
class Solution {
public:TreeNode* mergeTrees(TreeNode* root1, TreeNode* root2) {if(!root1) return root2;if(!root2) return root1;queue<TreeNode*> que;que.push(root1);que.push(root2);while(!que.empty()) {TreeNode *node1 = que.front();que.pop();TreeNode *node2 = que.front();que.pop();node1->val += node2->val;if(node1->left && node2->left) {que.push(node1->left);que.push(node2->left);}if(node1->right && node2->right) {que.push(node1->right);que.push(node2->right);}if(!node1->left && node2->left) {node1->left = node2->left;}if(!node1->right && node2->right) {node1->right = node2->right;}}return root1;}
};)




Unity内置的函数)









—— 基本概念和消息类型)



