PSO算法

粒子群算法（Particle,Swarm Optimization,PSO）由Kennedy和Eberhart于1995年提出，算法模仿鸟群觅食行为对优化问题进行求解。

粒子群算法中每个粒子包含位置和速度两个属性，其中，位置代表了待求问题的一个候选解，速度决定了粒子飞行的方向和距离。

1. 位置向量
   $$X_i^t=(x_{i1}^t,x_{i2}^t,\cdots x_{i,D}^t)\text{\hspace{1em}(1)}$$
2. 速度向量
   $$V_i^t=(v_{i1}^t,v_{i2}^t,\cdots v_{i,D}^t)\text{\hspace{1em}(2)}$$

算法超参数

• $w$：惯性权重，表示粒子在下一次迭代中应在多大程度上保持先前的运动方向和速度；
• $c_1$：个体学习因子，表示粒子在下一次迭代中飞向自己到过的最优位置的意愿；
• $c_2$：社会学习因子，表示粒子在下一次迭代中飞向群体到过的最优位置的意愿；
• NP：种群大小；
• Gmax：最大迭代数。

寻优公式

PSO通过粒子追随自己当前找到的个体最优解（pbest）和群体最优解（gbest）来完成优化。

• 速度更新：
  $$V_i^{t+1}=w{V}_i^t+c_1{r}_1(pbes{t}_i^t-x_i^t)+c_2{r}_2(gbes{t}^t-x_i^t)\text{\hspace{1em}(3)}$$
  其中，$pbes{t}_i^t$表示前$t$轮迭代中第$i$个粒子的最好位置，$gbes{t}^t$表示前$t$轮迭代中所有粒子的最好位置。$r_1,r_2$是D维向量，每一维元素是在[0,1]区间上均匀分布的随机数。
• 位置更新
  $$X_i^{t+1}=X_i^t+V_i^{t+1}\text{\hspace{1em}(4)}$$

初始化

初始解应当覆盖整个搜索空间，一般采用均匀分布随机生成初始解。
$$x_{ij}^0=x_{i,j}^{min}+rand(0,1)\cdot (x_{i,j}^{max}-x_{i,j}^{min})\text{\hspace{1em}(5)}$$
其中，rand(0,1)表示0-1之间的随机数，$x_{ij}^{max}$和$x_{ij}^{min}$分别表示该问题第j个维度变量的上下界。

伪代码

---

输入:超参数$(w,c_1,c_2,NP,Gmax)$和搜索边界$X_{min}$，$X_{max}$
输出:最优解
1:初始化
2:根据式(5)初始化位置种群X和速度种群V
3:记录个体最优pbest和群体最优gbest
4:优化搜索
5:For G = 1:Gmax
6: \qquad For i = 1:NP
7: \qquad \qquad 根据式(3)更新速度向量$V_i^G$
8: \qquad \qquad 根据式(4)更新位置向量$X_i^G$
9: \qquad \qquad If $f(X_i^G)<pbes{t}_i$
10: \qquad \qquad \qquad $pbes{t}_i=f(X_i^G)$
11: \qquad \qquad End
12: \qquad End
13: \qquad 更新群体最优$gbest$
14:End

---

注：优化算法并不保证能够得到问题的最优解，因此，算法输出的最优解并非问题的整体最优解，而是搜索过程中最好的一个解。

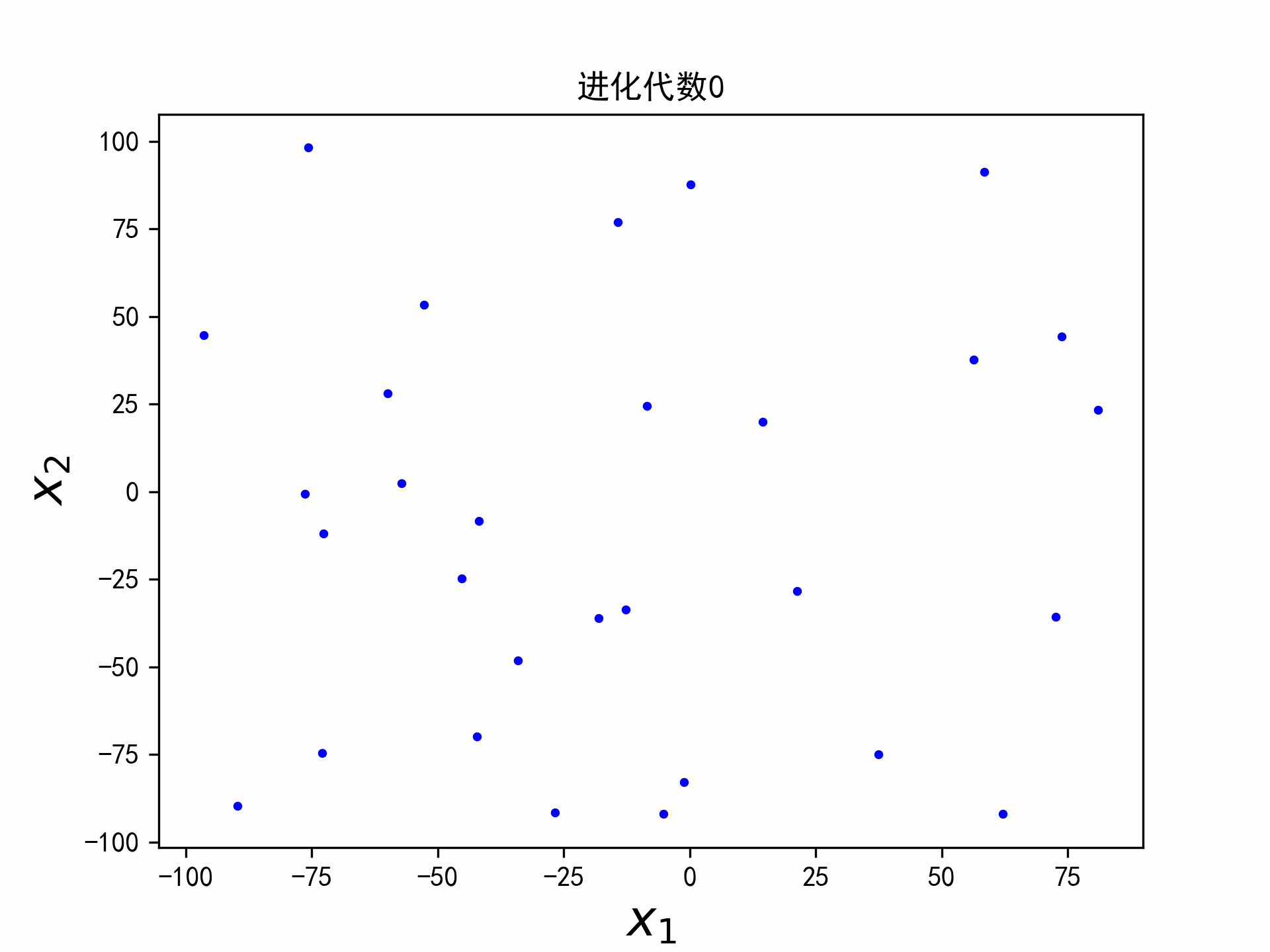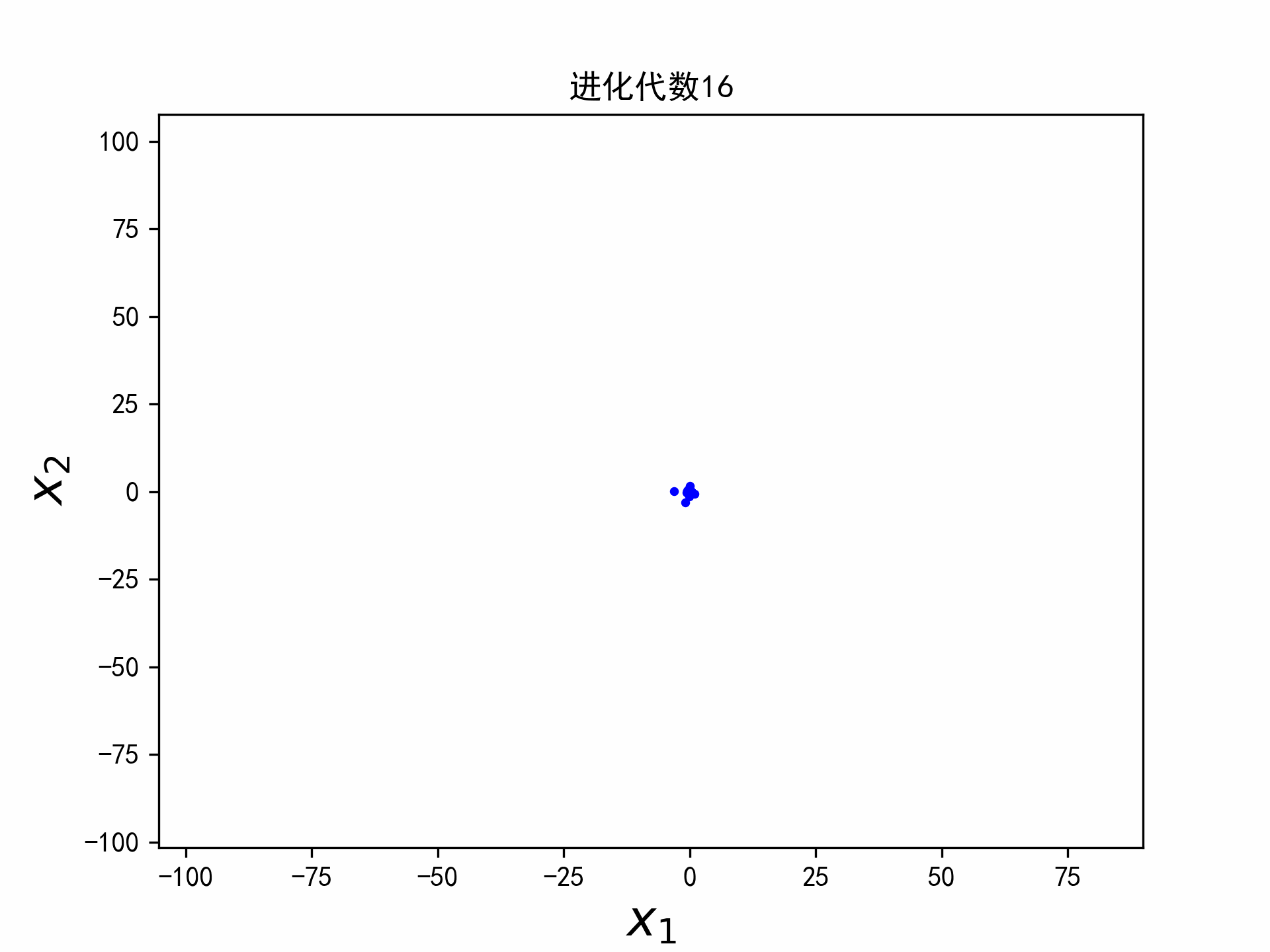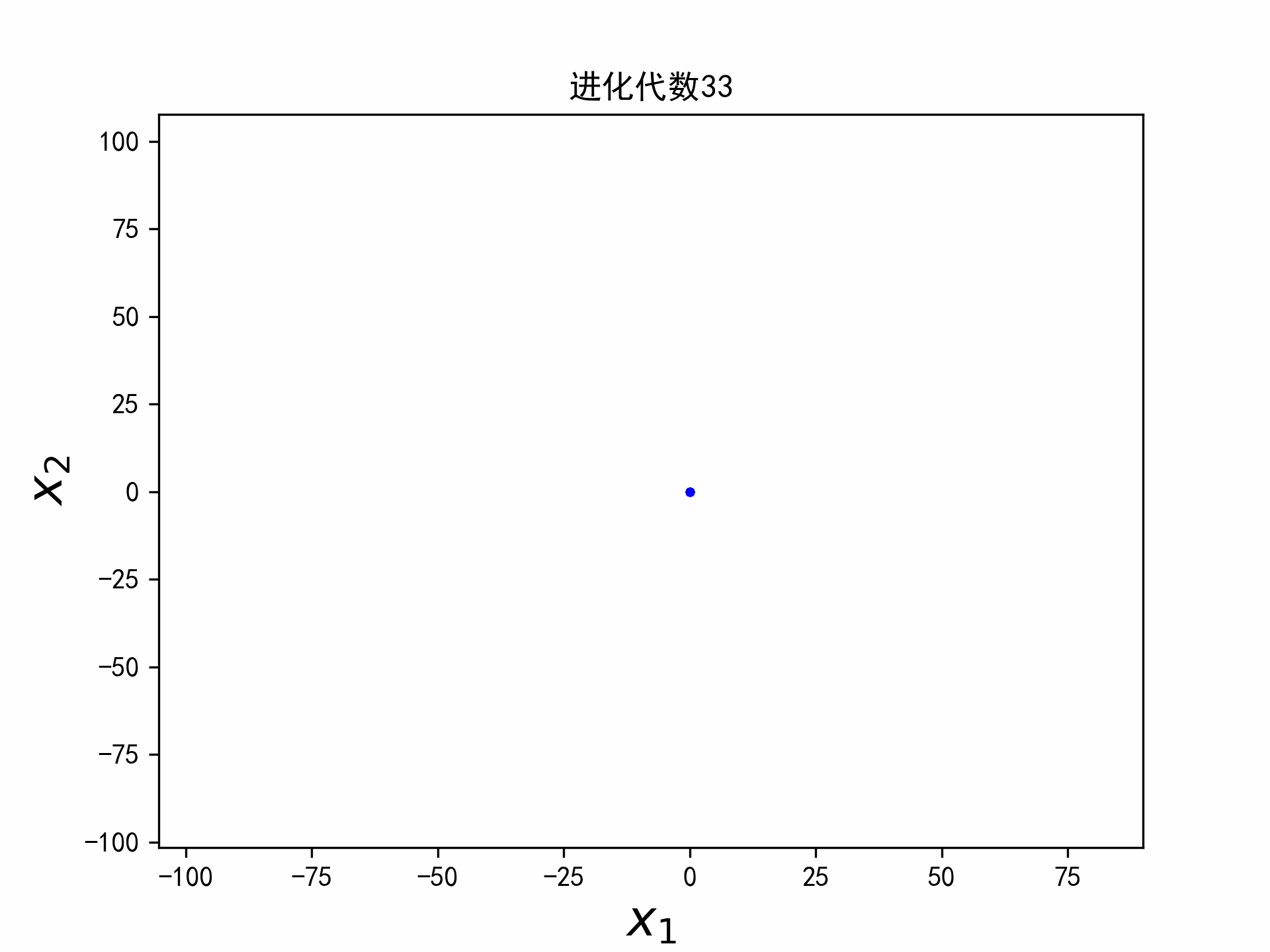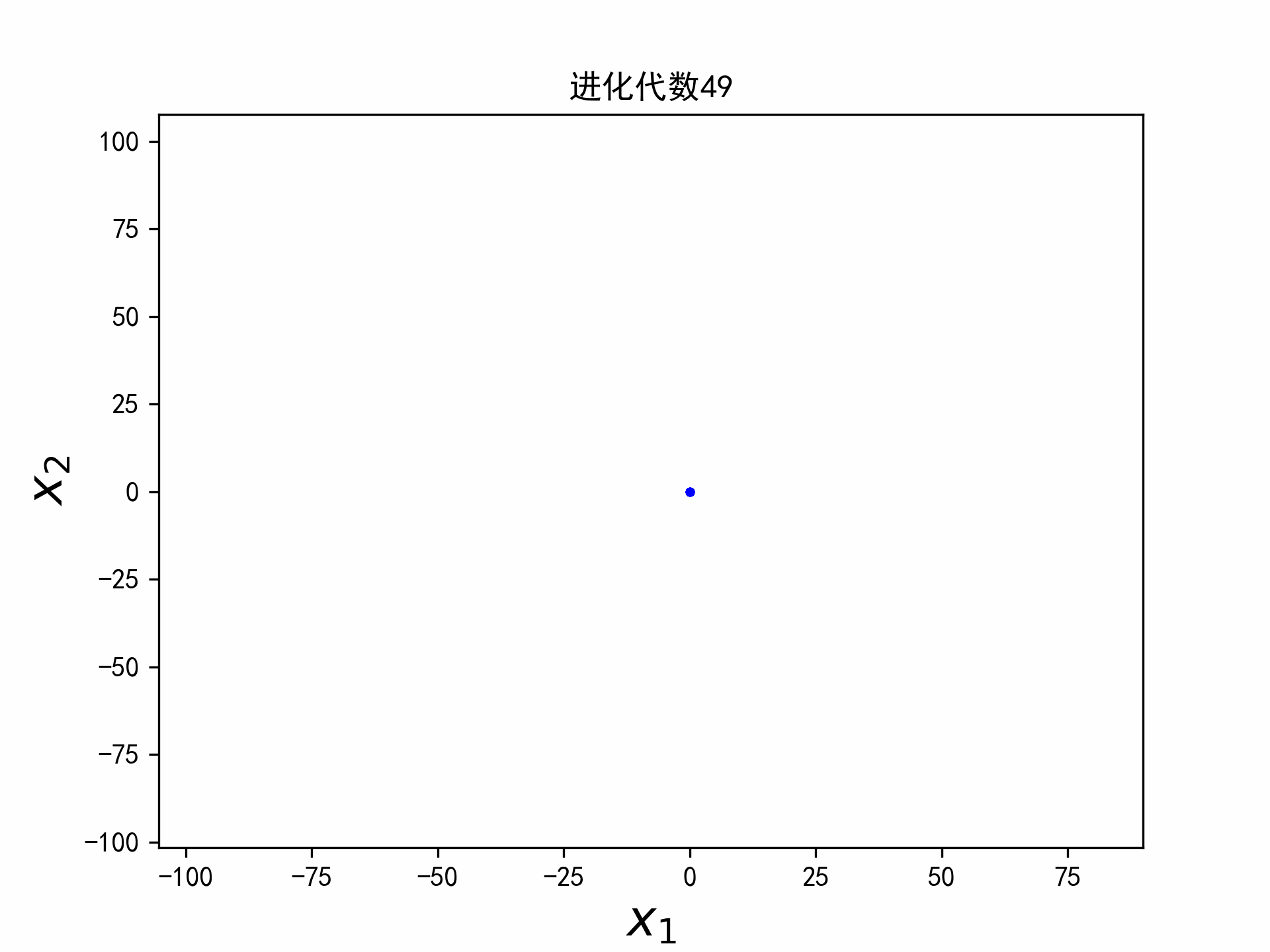
实验

实验选取二维的平方和函数，函数的最小值在点(a,b)取得，最小值为0。
$$f(x_1,x_2)=(x_1-a{)}^2+(x_2-b{)}^2\text{\hspace{1em}(6)}$$

实验参数如下：

参数	值
问题维度D	2
种群数NP	30
最大进化次数Gmax	50
惯性系数$w$	0.5
个体学习因子$c_1$	1
社会学习因子$c_2$	1
取值范围	(-100,100)

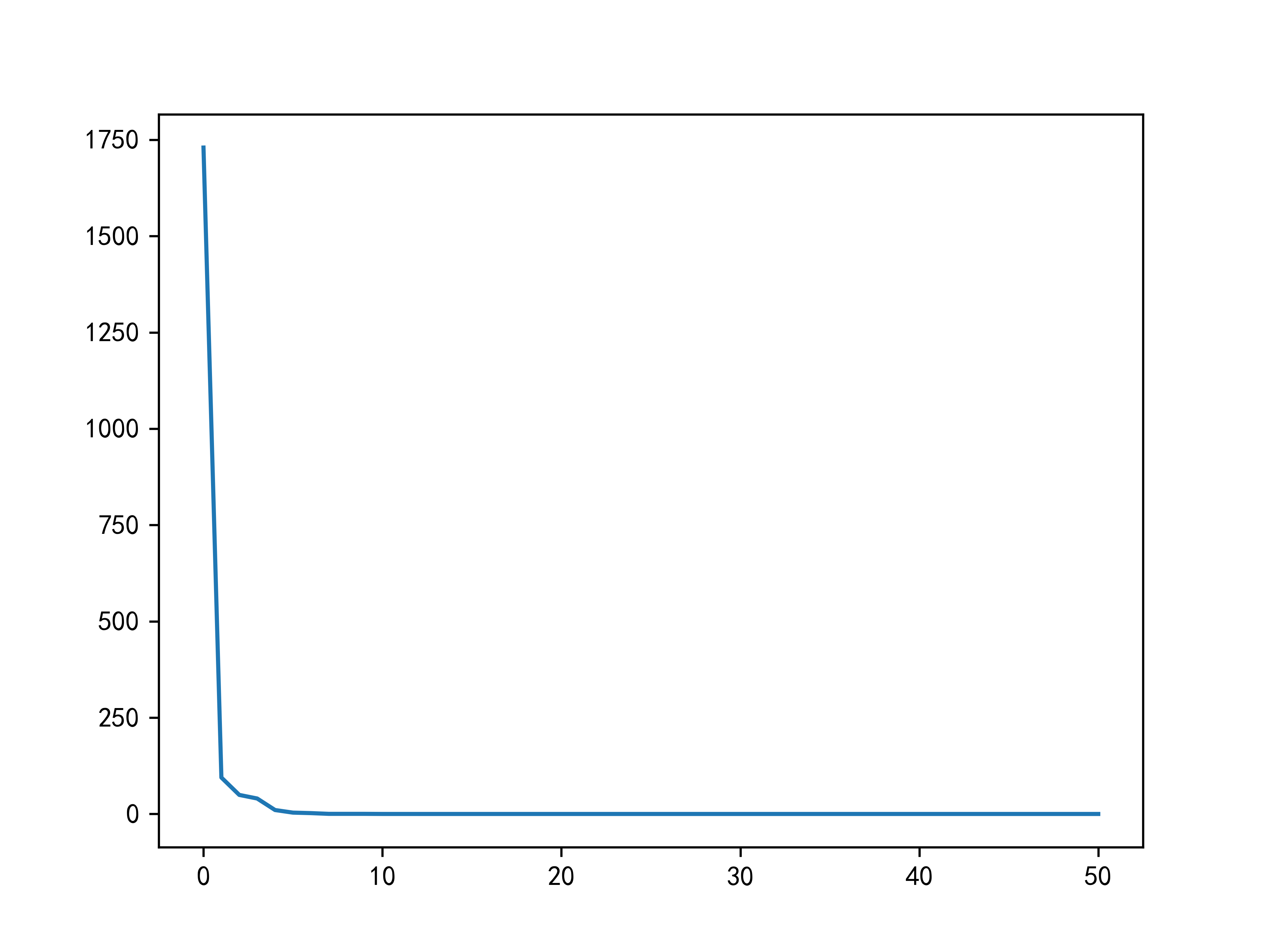
最优值	最差值	平均值	标准差
6.663e-14	4.767e-12	6.490e-13	9.266e-13

代码获取

关注微信公众号数学模型与算法回复 粒子群算法获取python代码

参考文献

[1] Storn R , Price K .Differential Evolution – A Simple and Efficient Heuristic for global Optimization over Continuous Spaces[J].Journal of Global Optimization, 1997, 11:341-359.DOI:10.1023/A:1008202821328.
[2] Das S , Abraham A , Chakraborty U K ,et al.Differential Evolution Using a Neighborhood-Based Mutation Operator[J].IEEE Transactions on Evolutionary Computation, 2009, 13(3):526-553.DOI:10.1109/TEVC.2008.2009457.