2859. 计算 K 置位下标对应元素的和
给你一个下标从 0 开始的整数数组 nums 和一个整数 k 。
请你用整数形式返回 nums 中的特定元素之 和 ,这些特定元素满足:其对应下标的二进制表示中恰存在 k 个置位。
整数的二进制表示中的 1 就是这个整数的 置位 。
例如,21 的二进制表示为 10101 ,其中有 3 个置位。
示例 1:
输入:nums = [5,10,1,5,2], k = 1
输出:13
解释:下标的二进制表示是:
0 = 0002
1 = 0012
2 = 0102
3 = 0112
4 = 1002
下标 1、2 和 4 在其二进制表示中都存在 k = 1 个置位。
因此,答案为 nums[1] + nums[2] + nums[4] = 13 。
示例 2:
输入:nums = [4,3,2,1], k = 2
输出:1
解释:下标的二进制表示是:
0 = 002
1 = 012
2 = 102
3 = 112
只有下标 3 的二进制表示中存在 k = 2 个置位。
因此,答案为 nums[3] = 1 。
提示:
1 <= nums.length <= 1000
1 <= nums[i] <= 1e5
0 <= k <= 10
简单模拟:
class Solution {
public:int sumIndicesWithKSetBits(vector<int>& nums, int k) {int len = nums.size();int ans = 0;if(len < 1) {return 0;}for(int i = 0;i < len;i++){int tmp = i;int count = 0;while(tmp > 0 && tmp != 1){if(tmp % 2 == 1) {count++;}tmp = tmp / 2;}if(tmp == 1) {count++;}if(count == k) {ans += nums[i];}}return ans;}
};
2846. 边权重均等查询(Hard)
现有一棵由 n 个节点组成的无向树,节点按从 0 到 n - 1 编号。给你一个整数 n 和一个长度为 n - 1 的二维整数数组 edges ,其中 edges[i] = [ui, vi, wi] 表示树中存在一条位于节点 ui 和节点 vi 之间、权重为 wi 的边。
另给你一个长度为 m 的二维整数数组 queries ,其中 queries[i] = [ai, bi] 。对于每条查询,请你找出使从 ai 到 bi 路径上每条边的权重相等所需的 最小操作次数 。在一次操作中,你可以选择树上的任意一条边,并将其权重更改为任意值。
注意:
查询之间 相互独立 的,这意味着每条新的查询时,树都会回到 初始状态 。
从 ai 到 bi的路径是一个由 不同 节点组成的序列,从节点 ai 开始,到节点 bi 结束,且序列中相邻的两个节点在树中共享一条边。
返回一个长度为 m 的数组 answer ,其中 answer[i] 是第 i 条查询的答案。
示例 1:
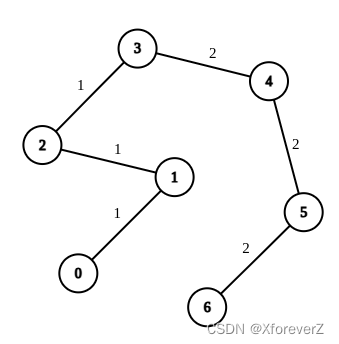
输入:n = 7, edges = [[0,1,1],[1,2,1],[2,3,1],[3,4,2],[4,5,2],[5,6,2]], queries = [[0,3],[3,6],[2,6],[0,6]]
输出:[0,0,1,3]
解释:第 1 条查询,从节点 0 到节点 3 的路径中的所有边的权重都是 1 。因此,答案为 0 。
第 2 条查询,从节点 3 到节点 6 的路径中的所有边的权重都是 2 。因此,答案为 0 。
第 3 条查询,将边 [2,3] 的权重变更为 2 。在这次操作之后,从节点 2 到节点 6 的路径中的所有边的权重都是 2 。因此,答案为 1 。
第 4 条查询,将边 [0,1]、[1,2]、[2,3] 的权重变更为 2 。在这次操作之后,从节点 0 到节点 6 的路径中的所有边的权重都是 2 。因此,答案为 3 。
对于每条查询 queries[i] ,可以证明 answer[i] 是使从 ai 到 bi 的路径中的所有边的权重相等的最小操作次数。
示例 2:
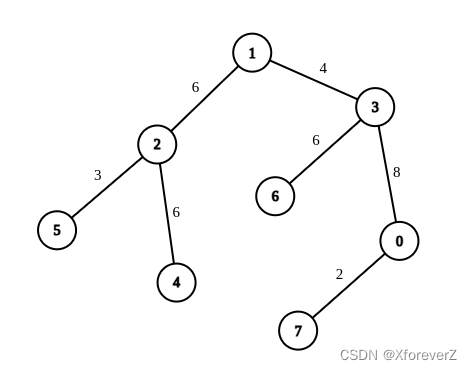
输入:n = 8, edges = [[1,2,6],[1,3,4],[2,4,6],[2,5,3],[3,6,6],[3,0,8],[7,0,2]], queries = [[4,6],[0,4],[6,5],[7,4]]
输出:[1,2,2,3]
解释:第 1 条查询,将边 [1,3] 的权重变更为 6 。在这次操作之后,从节点 4 到节点 6 的路径中的所有边的权重都是 6 。因此,答案为 1 。
第 2 条查询,将边 [0,3]、[3,1] 的权重变更为 6 。在这次操作之后,从节点 0 到节点 4 的路径中的所有边的权重都是 6 。因此,答案为 2 。
第 3 条查询,将边 [1,3]、[5,2] 的权重变更为 6 。在这次操作之后,从节点 6 到节点 5 的路径中的所有边的权重都是 6 。因此,答案为 2 。
第 4 条查询,将边 [0,7]、[0,3]、[1,3] 的权重变更为 6 。在这次操作之后,从节点 7 到节点 4 的路径中的所有边的权重都是 6 。因此,答案为 3 。
对于每条查询 queries[i] ,可以证明 answer[i] 是使从 ai 到 bi 的路径中的所有边的权重相等的最小操作次数。
提示:
1 <= n <= 1e4
edges.length == n - 1
edges[i].length == 3
0 <= ui, vi < n
1 <= wi <= 26
生成的输入满足 edges 表示一棵有效的树
1 <= queries.length == m <= 2 * 1e4
queries[i].length == 2
0 <= ai, bi < n
这题用到LCA 以前没有了解过,这里照搬灵神题解,有时间可以出个专项练习题集:
class Solution {
public:vector<int> minOperationsQueries(int n, vector<vector<int>> &edges, vector<vector<int>> &queries) {vector<vector<pair<int, int>>> g(n);for (auto &e: edges) {int x = e[0], y = e[1], w = e[2] - 1;g[x].emplace_back(y, w);g[y].emplace_back(x, w);}int m = 32 - __builtin_clz(n); // n 的二进制长度vector<vector<int>> pa(n, vector<int>(m, -1));vector<vector<array<int, 26>>> cnt(n, vector<array<int, 26>>(m));vector<int> depth(n);function<void(int, int)> dfs = [&](int x, int fa) {pa[x][0] = fa;for (auto [y, w]: g[x]) {if (y != fa) {cnt[y][0][w] = 1;depth[y] = depth[x] + 1;dfs(y, x);}}};dfs(0, -1);for (int i = 0; i < m - 1; i++) {for (int x = 0; x < n; x++) {int p = pa[x][i];if (p != -1) {int pp = pa[p][i];pa[x][i + 1] = pp;for (int j = 0; j < 26; ++j) {cnt[x][i + 1][j] = cnt[x][i][j] + cnt[p][i][j];}}}}vector<int> ans;for (auto &q: queries) {int x = q[0], y = q[1];int path_len = depth[x] + depth[y]; // 最后减去 depth[lca] * 2int cw[26]{};if (depth[x] > depth[y]) {swap(x, y);}// 让 y 和 x 在同一深度for (int k = depth[y] - depth[x]; k; k &= k - 1) {int i = __builtin_ctz(k);int p = pa[y][i];for (int j = 0; j < 26; ++j) {cw[j] += cnt[y][i][j];}y = p;}if (y != x) {for (int i = m - 1; i >= 0; i--) {int px = pa[x][i], py = pa[y][i];if (px != py) {for (int j = 0; j < 26; j++) {cw[j] += cnt[x][i][j] + cnt[y][i][j];}x = px;y = py; // x 和 y 同时上跳 2^i 步}}for (int j = 0; j < 26; j++) {cw[j] += cnt[x][0][j] + cnt[y][0][j];}x = pa[x][0];}int lca = x;path_len -= depth[lca] * 2;ans.push_back(path_len - *max_element(cw, cw + 26));}return ans;}
};
题解:LCA 模板
2861. 最大合金数
假设你是一家合金制造公司的老板,你的公司使用多种金属来制造合金。现在共有 n 种不同类型的金属可以使用,并且你可以使用 k 台机器来制造合金。每台机器都需要特定数量的每种金属来创建合金。
对于第 i 台机器而言,创建合金需要 composition[i][j] 份 j 类型金属。最初,你拥有 stock[i] 份 i 类型金属,而每购入一份 i 类型金属需要花费 cost[i] 的金钱。
给你整数 n、k、budget,下标从 1 开始的二维数组 composition,两个下标从 1 开始的数组 stock 和 cost,请你在预算不超过 budget 金钱的前提下,最大化 公司制造合金的数量。
所有合金都需要由同一台机器制造。
返回公司可以制造的最大合金数。
示例 1:
输入:n = 3, k = 2, budget = 15, composition = [[1,1,1],[1,1,10]], stock = [0,0,0], cost = [1,2,3]
输出:2
解释:最优的方法是使用第 1 台机器来制造合金。
要想制造 2 份合金,我们需要购买:
- 2 份第 1 类金属。
- 2 份第 2 类金属。
- 2 份第 3 类金属。
总共需要 2 * 1 + 2 * 2 + 2 * 3 = 12 的金钱,小于等于预算 15 。
注意,我们最开始时候没有任何一类金属,所以必须买齐所有需要的金属。
可以证明在示例条件下最多可以制造 2 份合金。
示例 2:
输入:n = 3, k = 2, budget = 15, composition = [[1,1,1],[1,1,10]], stock = [0,0,100], cost = [1,2,3]
输出:5
解释:最优的方法是使用第 2 台机器来制造合金。
要想制造 5 份合金,我们需要购买:
- 5 份第 1 类金属。
- 5 份第 2 类金属。
- 0 份第 3 类金属。
总共需要 5 * 1 + 5 * 2 + 0 * 3 = 15 的金钱,小于等于预算 15 。
可以证明在示例条件下最多可以制造 5 份合金。
示例 3:
输入:n = 2, k = 3, budget = 10, composition = [[2,1],[1,2],[1,1]], stock = [1,1], cost = [5,5]
输出:2
解释:最优的方法是使用第 3 台机器来制造合金。
要想制造 2 份合金,我们需要购买:
- 1 份第 1 类金属。
- 1 份第 2 类金属。
总共需要 1 * 5 + 1 * 5 = 10 的金钱,小于等于预算 10 。
可以证明在示例条件下最多可以制造 2 份合金。
提示:
1 <= n, k <= 100
0 <= budget <= 1e8
composition.length == k
composition[i].length == n
1 <= composition[i][j] <= 100
stock.length == cost.length == n
0 <= stock[i] <= 1e8
1 <= cost[i] <= 100
二分解法,思路清楚后不难:
class Solution {
public:int maxNumberOfAlloys(int n, int k, int b, vector<vector<int>>& a,vector<int>& s, vector<int>& c) {long long l = 0, r = 2 * 1e8 + 5, mid, ans = 0;while (l <= r) {mid = (l + r) / 2;if (se(n, k, b, mid, a, s, c)) {ans = max(ans, mid);l = mid + 1;} elser = mid - 1;}return ans;}bool se(int n, int k, int b, long long x, vector<vector<int>>& a,vector<int>& s, vector<int>& c) {long long sum, t = 0;for (int i = 0; i < k; i++) {sum = 0;for (int j = 0; j < n; j++) {long long ne = max(t, a[i][j] * x - s[j]);sum += ne * c[j];}if (sum <= b)return 1;}return 0;}
};
365. 水壶问题
有两个水壶,容量分别为 jug1Capacity 和 jug2Capacity 升。水的供应是无限的。确定是否有可能使用这两个壶准确得到 targetCapacity 升。
如果可以得到 targetCapacity 升水,最后请用以上水壶中的一或两个来盛放取得的 targetCapacity 升水。
你可以:
装满任意一个水壶
清空任意一个水壶
从一个水壶向另外一个水壶倒水,直到装满或者倒空
示例 1:
输入: jug1Capacity = 3, jug2Capacity = 5, targetCapacity = 4
输出: true
解释:来自著名的 “Die Hard”
示例 2:
输入: jug1Capacity = 2, jug2Capacity = 6, targetCapacity = 5
输出: false
示例 3:
输入: jug1Capacity = 1, jug2Capacity = 2, targetCapacity = 3
输出: true
提示:
1 <= jug1Capacity, jug2Capacity, targetCapacity <= 1e6
又是一种我没了解过的算法GCD(贝祖定理),看了题解了解一点后尝试了一下,并不难:
class Solution {
public:bool canMeasureWater(int x, int y, int z) {if (z == 0)return true;if (z < 0 || z > x + y)return false;int GCD = gcd(x, y);return !(z % GCD);}
};
514. 自由之路(Hard)
电子游戏“辐射4”中,任务 “通向自由” 要求玩家到达名为 “Freedom Trail Ring” 的金属表盘,并使用表盘拼写特定关键词才能开门。
给定一个字符串 ring ,表示刻在外环上的编码;给定另一个字符串 key ,表示需要拼写的关键词。您需要算出能够拼写关键词中所有字符的最少步数。
最初,ring 的第一个字符与 12:00 方向对齐。您需要顺时针或逆时针旋转 ring 以使 key 的一个字符在 12:00 方向对齐,然后按下中心按钮,以此逐个拼写完 key 中的所有字符。
旋转 ring 拼出 key 字符 key[i] 的阶段中:
您可以将 ring 顺时针或逆时针旋转 一个位置 ,计为1步。旋转的最终目的是将字符串 ring 的一个字符与 12:00 方向对齐,并且这个字符必须等于字符 key[i] 。
如果字符 key[i] 已经对齐到12:00方向,您需要按下中心按钮进行拼写,这也将算作 1 步。按完之后,您可以开始拼写 key 的下一个字符(下一阶段), 直至完成所有拼写。
示例 1:
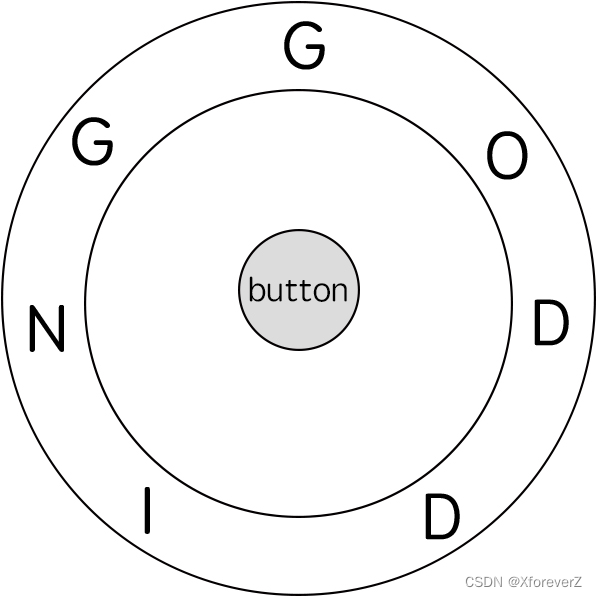
输入: ring = “godding”, key = “gd”
输出: 4
解释:
对于 key 的第一个字符 ‘g’,已经在正确的位置, 我们只需要1步来拼写这个字符。
对于 key 的第二个字符 ‘d’,我们需要逆时针旋转 ring “godding” 2步使它变成 “ddinggo”。
当然, 我们还需要1步进行拼写。
因此最终的输出是 4。
示例 2:
输入: ring = “godding”, key = “godding”
输出: 13
提示:
1 <= ring.length, key.length <= 100
ring 和 key 只包含小写英文字母
保证 字符串 key 一定可以由字符串 ring 旋转拼出
DFS做法:
class Solution {
public:vector<vector<int>> memo;int findRotateSteps(string ring, string key) {memo.assign(ring.size(), vector<int>(key.size(), -1));return dfs(ring, 0, key, 0) + key.size();}int dfs(string ring, int i, string key, int j) {int n = ring.size(), m = key.size();if (j == key.size()) {return 0;}if (memo[i][j] != -1)return memo[i][j];int step = INT_MAX;for (int p = 0; p < ring.size(); p++) {if (ring[p] == key[j]) {step = min(step, dfs(ring, p, key, j + 1) +min(abs(p - i), n - abs(p - i)));}}memo[i][j] = step;return memo[i][j];}
};
题解中还有DP/BFS做法,可以了解一下:
两种 O(nm) 做法:DP / BFS
2808. 使循环数组所有元素相等的最少秒数
给你一个下标从 0 开始长度为 n 的数组 nums 。
每一秒,你可以对数组执行以下操作:
对于范围在 [0, n - 1] 内的每一个下标 i ,将 nums[i] 替换成 nums[i] ,nums[(i - 1 + n) % n] 或者 nums[(i + 1) % n] 三者之一。
注意,所有元素会被同时替换。
请你返回将数组 nums 中所有元素变成相等元素所需要的 最少 秒数。
示例 1:
输入:nums = [1,2,1,2]
输出:1
解释:我们可以在 1 秒内将数组变成相等元素:
- 第 1 秒,将每个位置的元素分别变为 [nums[3],nums[1],nums[3],nums[3]] 。变化后,nums = [2,2,2,2] 。
1 秒是将数组变成相等元素所需要的最少秒数。
示例 2:
输入:nums = [2,1,3,3,2]
输出:2
解释:我们可以在 2 秒内将数组变成相等元素:
- 第 1 秒,将每个位置的元素分别变为 [nums[0],nums[2],nums[2],nums[2],nums[3]] 。变化后,nums = [2,3,3,3,3] 。
- 第 2 秒,将每个位置的元素分别变为 [nums[1],nums[1],nums[2],nums[3],nums[4]] 。变化后,nums = [3,3,3,3,3] 。
2 秒是将数组变成相等元素所需要的最少秒数。
示例 3:
输入:nums = [5,5,5,5]
输出:0
解释:不需要执行任何操作,因为一开始数组中的元素已经全部相等。
提示:
1 <= n == nums.length <= 1e5
1 <= nums[i] <= 1e9
哈希,看了题解后才有了比较清晰的思路,膜拜各路大佬orz:
class Solution {
public:int minimumSeconds(vector<int>& nums) {unordered_map<int, vector<int>> pos_hash;int n = nums.size();for (int i = 0; i < n; i++) {pos_hash[nums[i]].push_back(i);}int ans = INT_MAX;for (auto pair : pos_hash) {int tmp_max = 0;int m = pair.second.size();for (int j = 0; j < m; j++) {tmp_max =max(tmp_max,(pair.second[(j + 1) % m] - pair.second[j] + n) % n);}if (m == 1) {tmp_max = n;}ans = min(ans, tmp_max / 2);}return ans;}
};
哈希表 + 统计:正难则反——将元素改变转为元素扩散【图解】
这个题解比较清晰
2670. 找出不同元素数目差数组
给你一个下标从 0 开始的数组 nums ,数组长度为 n 。
nums 的 不同元素数目差 数组可以用一个长度为 n 的数组 diff 表示,其中 diff[i] 等于前缀 nums[0, …, i] 中不同元素的数目 减去 后缀 nums[i + 1, …, n - 1] 中不同元素的数目。
返回 nums 的 不同元素数目差 数组。
注意 nums[i, …, j] 表示 nums 的一个从下标 i 开始到下标 j 结束的子数组(包含下标 i 和 j 对应元素)。特别需要说明的是,如果 i > j ,则 nums[i, …, j] 表示一个空子数组。
示例 1:
输入:nums = [1,2,3,4,5]
输出:[-3,-1,1,3,5]
解释:
对于 i = 0,前缀中有 1 个不同的元素,而在后缀中有 4 个不同的元素。因此,diff[0] = 1 - 4 = -3 。
对于 i = 1,前缀中有 2 个不同的元素,而在后缀中有 3 个不同的元素。因此,diff[1] = 2 - 3 = -1 。
对于 i = 2,前缀中有 3 个不同的元素,而在后缀中有 2 个不同的元素。因此,diff[2] = 3 - 2 = 1 。
对于 i = 3,前缀中有 4 个不同的元素,而在后缀中有 1 个不同的元素。因此,diff[3] = 4 - 1 = 3 。
对于 i = 4,前缀中有 5 个不同的元素,而在后缀中有 0 个不同的元素。因此,diff[4] = 5 - 0 = 5 。
示例 2:
输入:nums = [3,2,3,4,2]
输出:[-2,-1,0,2,3]
解释:
对于 i = 0,前缀中有 1 个不同的元素,而在后缀中有 3 个不同的元素。因此,diff[0] = 1 - 3 = -2 。
对于 i = 1,前缀中有 2 个不同的元素,而在后缀中有 3 个不同的元素。因此,diff[1] = 2 - 3 = -1 。
对于 i = 2,前缀中有 2 个不同的元素,而在后缀中有 2 个不同的元素。因此,diff[2] = 2 - 2 = 0 。
对于 i = 3,前缀中有 3 个不同的元素,而在后缀中有 1 个不同的元素。因此,diff[3] = 3 - 1 = 2 。
对于 i = 4,前缀中有 3 个不同的元素,而在后缀中有 0 个不同的元素。因此,diff[4] = 3 - 0 = 3 。
提示:
1 <= n == nums.length <= 50
1 <= nums[i] <= 50
前后缀分解:
class Solution {
public:vector<int> distinctDifferenceArray(vector<int>& nums) {int n = nums.size(), suf[n + 1];suf[n] = 0;unordered_set<int> s;for (int i = n - 1; i; i--) {s.insert(nums[i]);suf[i] = s.size();}s.clear();vector<int> ans(n);for (int i = 0; i < n; i++) {s.insert(nums[i]);ans[i] = s.size() - suf[i + 1];}return ans;}
};
LCP 24. 数字游戏
小扣在秋日市集入口处发现了一个数字游戏。主办方共有 N 个计数器,计数器编号为 0 ~ N-1。每个计数器上分别显示了一个数字,小扣按计数器编号升序将所显示的数字记于数组 nums。每个计数器上有两个按钮,分别可以实现将显示数字加一或减一。小扣每一次操作可以选择一个计数器,按下加一或减一按钮。
主办方请小扣回答出一个长度为 N 的数组,第 i 个元素(0 <= i < N)表示将 0~i 号计数器 初始 所示数字操作成满足所有条件 nums[a]+1 == nums[a+1],(0 <= a < i) 的最小操作数。回答正确方可进入秋日市集。
由于答案可能很大,请将每个最小操作数对 1,000,000,007 取余。
示例 1:
输入:nums = [3,4,5,1,6,7]
输出:[0,0,0,5,6,7]
解释: i = 0,[3] 无需操作 i = 1,[3,4] 无需操作; i = 2,[3,4,5] 无需操作; i = 3,将 [3,4,5,1] 操作成 [3,4,5,6], 最少 5 次操作; i = 4,将 [3,4,5,1,6] 操作成 [3,4,5,6,7], 最少 6 次操作; i = 5,将 [3,4,5,1,6,7] 操作成 [3,4,5,6,7,8],最少 7 次操作; 返回 [0,0,0,5,6,7]。
示例 2:
输入:nums = [1,2,3,4,5]
输出:[0,0,0,0,0]
解释:对于任意计数器编号 i 都无需操作。
示例 3:
输入:nums = [1,1,1,2,3,4]
输出:[0,1,2,3,3,3]
解释: i = 0,无需操作; i = 1,将 [1,1] 操作成 [1,2] 或 [0,1] 最少 1 次操作; i = 2,将 [1,1,1] 操作成 [1,2,3] 或 [0,1,2],最少 2 次操作; i = 3,将 [1,1,1,2] 操作成 [1,2,3,4] 或 [0,1,2,3],最少 3 次操作; i = 4,将 [1,1,1,2,3] 操作成 [-1,0,1,2,3],最少 3 次操作; i = 5,将 [1,1,1,2,3,4] 操作成 [-1,0,1,2,3,4],最少 3 次操作; 返回 [0,1,2,3,3,3]。
提示:
1 <= nums.length <= 10^5
1 <= nums[i] <= 10^3
这个好难不会做…
参考灵神题解:
class Solution {
public:vector<int> numsGame(vector<int>& nums) {const int MOD = 1'000'000'007;vector<int> ans(nums.size());priority_queue<int> left; // 维护较小的一半,大根堆priority_queue<int, vector<int>, greater<int>>right; // 维护较大的一半,小根堆long long left_sum = 0, right_sum = 0;for (int i = 0; i < nums.size(); i++) {int b = nums[i] - i;if (i % 2 == 0) { // 前缀长度是奇数if (!left.empty() && b < left.top()) {left_sum -= left.top() - b;left.push(b);b = left.top();left.pop();}right_sum += b;right.push(b);ans[i] = (right_sum - right.top() - left_sum) % MOD;} else { // 前缀长度是偶数if (b > right.top()) {right_sum += b - right.top();right.push(b);b = right.top();right.pop();}left_sum += b;left.push(b);ans[i] = (right_sum - left_sum) % MOD;}}return ans;}
};
转换+中位数贪心+对顶堆




异常)

)







----死锁)




)