正常状态
绿色方块:刚体+碰撞盒+检测触发碰撞脚本
蓝色方块:碰撞盒
检测脚本:

正常进出:
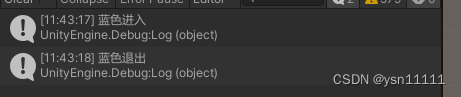
踩坑1
绿色方块:刚体+碰撞盒+检测触发碰撞脚本
蓝色方块:碰撞盒
保持绿色和蓝色方块的接触

对蓝色方块:显示->隐藏不会有任何效果,隐藏->显示会触发OnTriggerEnter
对蓝色方块:激活->未激活,不会有任何效果,未激活->激活会触发OnTriggerEnter
销毁蓝色方块:不会有任何效果。
通过代码将蓝色方块瞬移到很远的地方,会触发OnTriggerEnter。
踩坑2
绿色方块:刚体+碰撞盒+检测触发碰撞脚本
蓝色方块:碰撞盒+刚体
我给蓝色方块加了刚体,保持接触的状态,勾选Is Kinematic
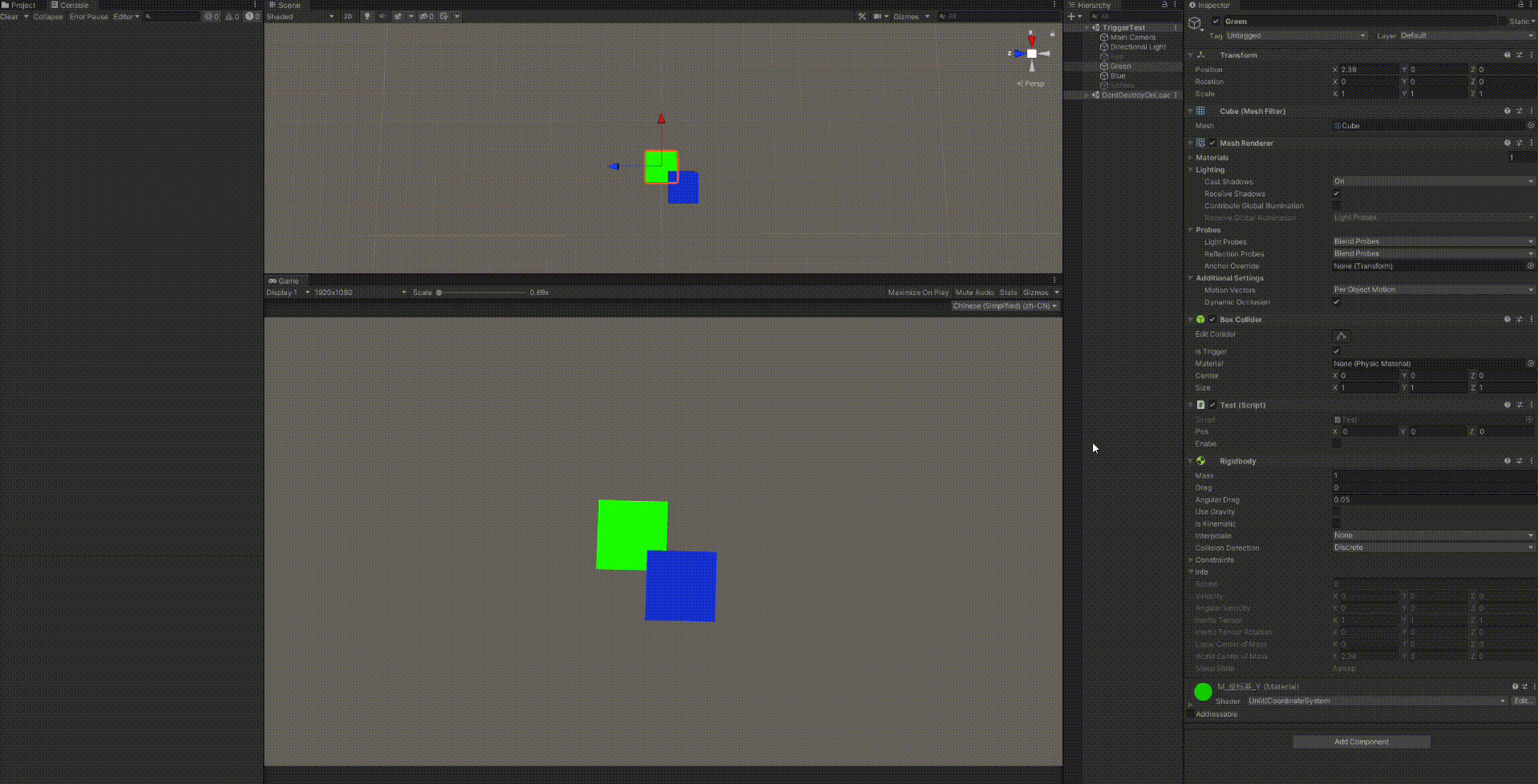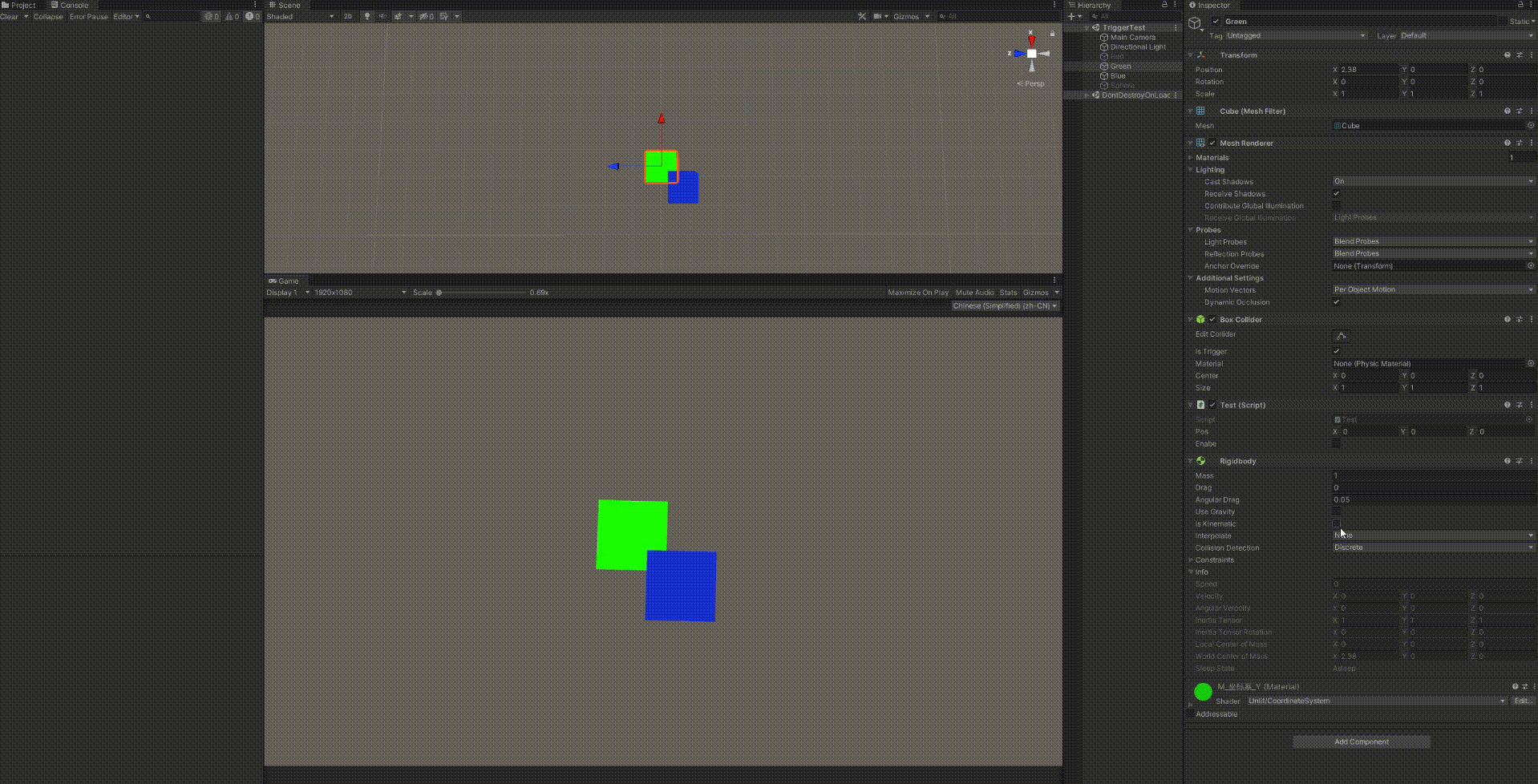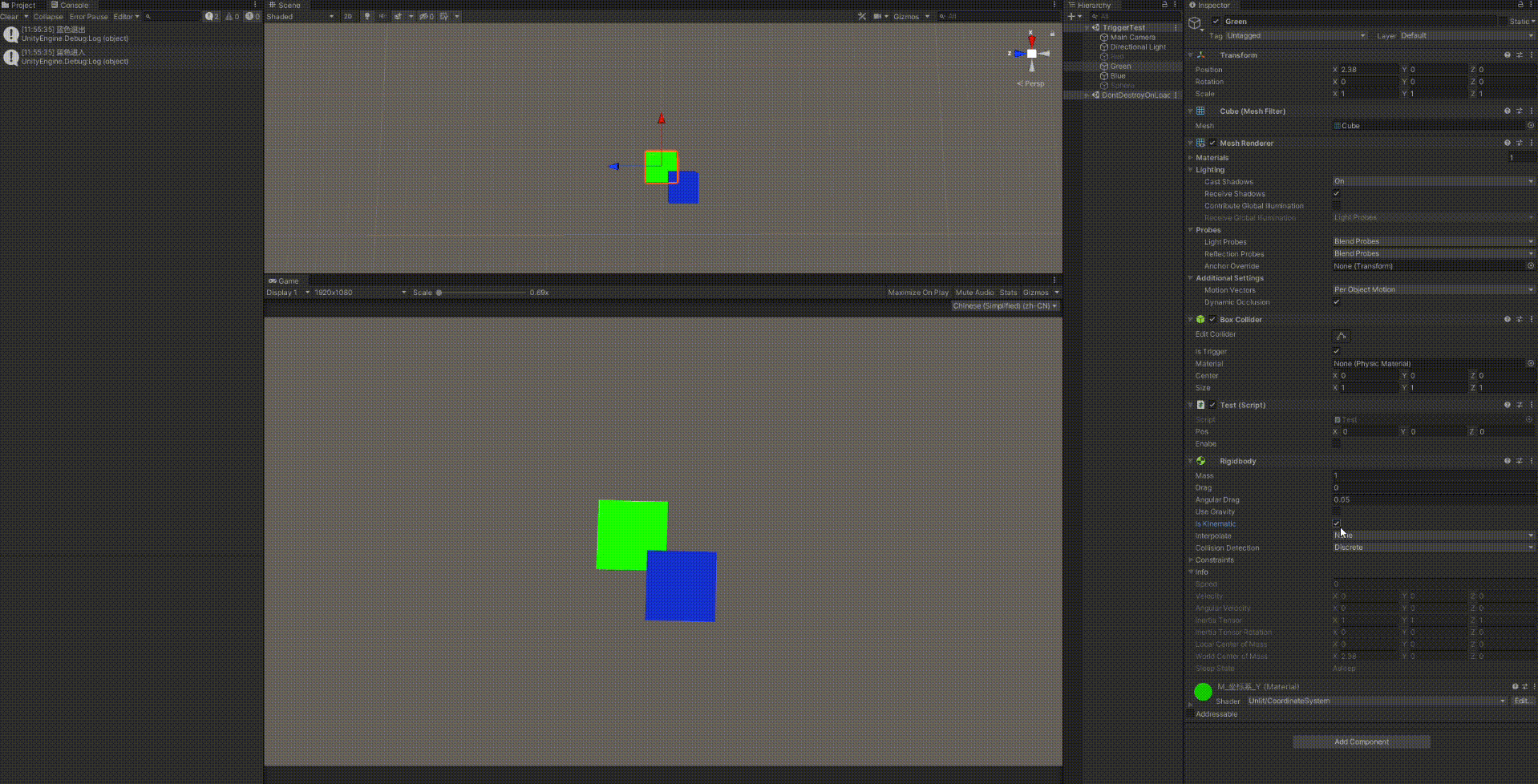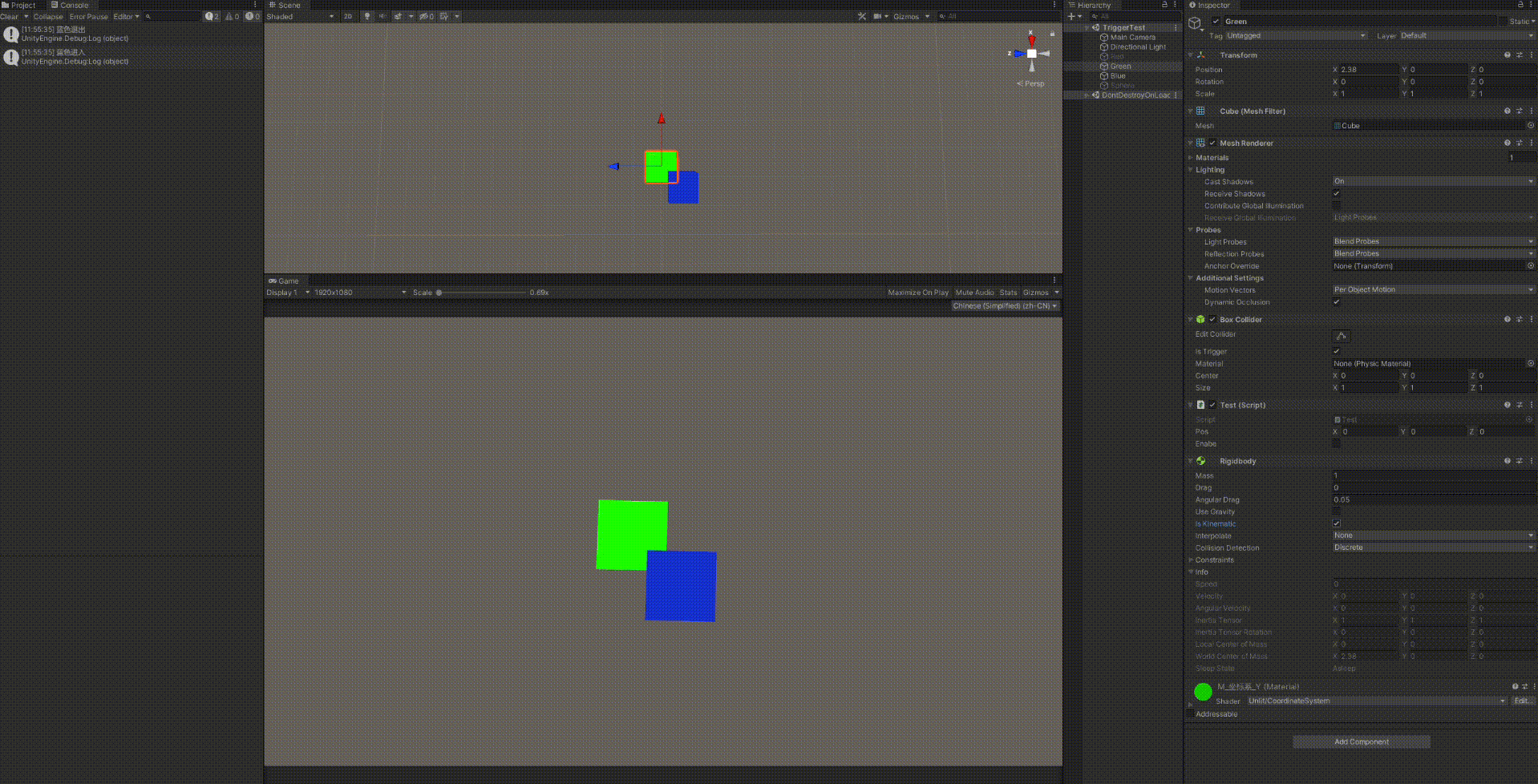

结果就是我切换Is Kinematic都会触发物理的重新检测,先退出再进入
踩坑3
白色小球:无碰撞盒,无刚体,无脚本
绿色方块:刚体+碰撞盒+检测触发碰撞脚本
蓝色方块:碰撞盒+刚体
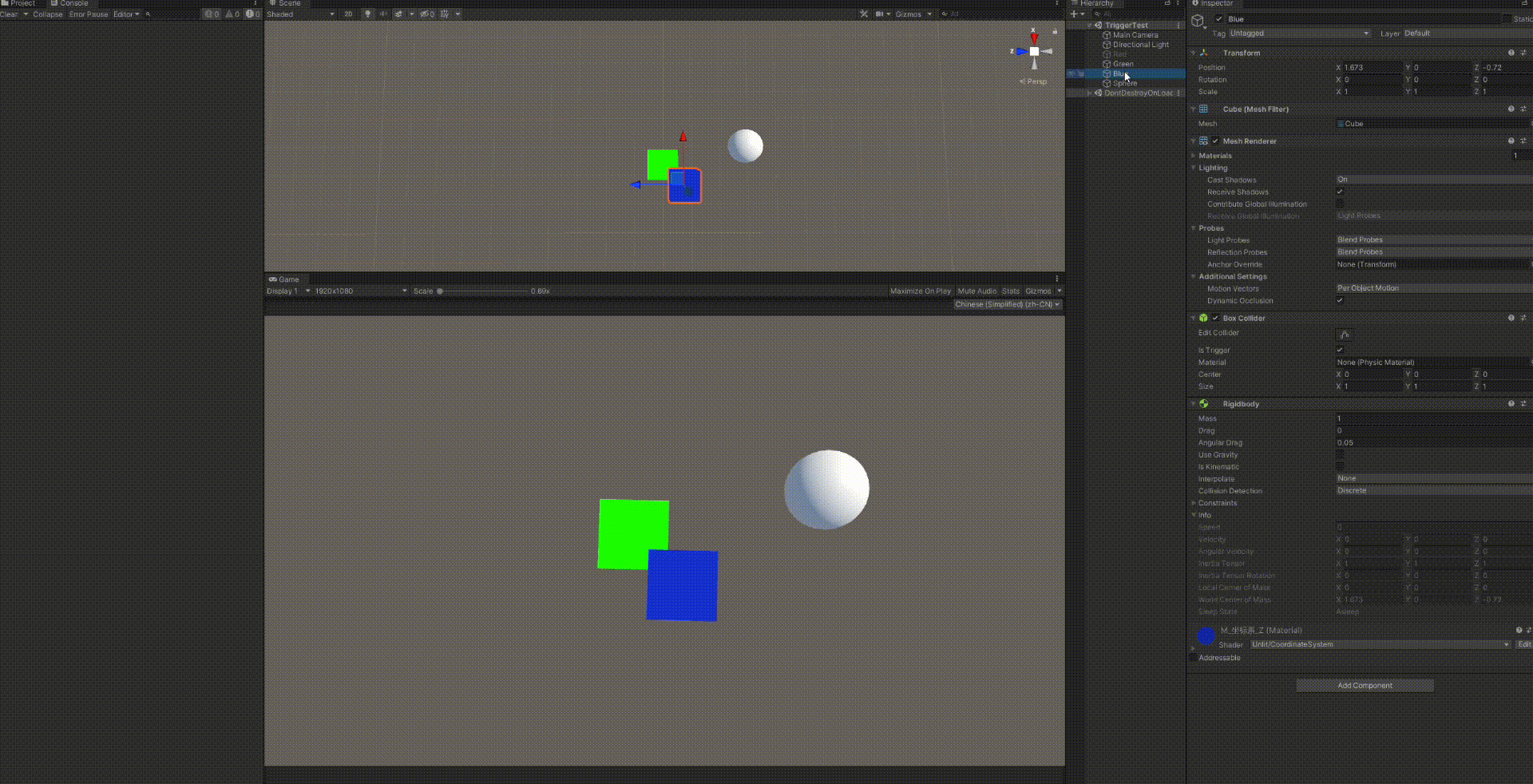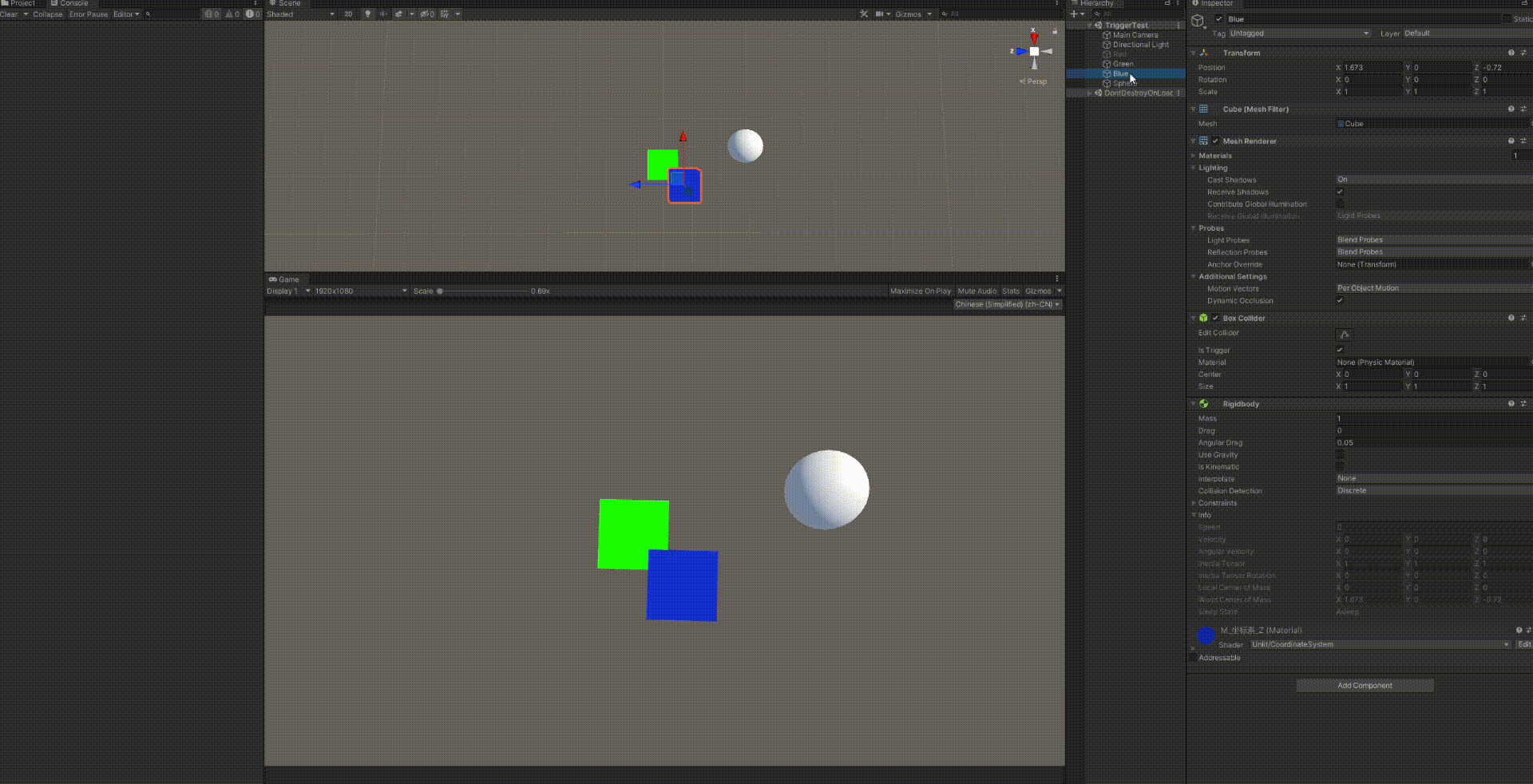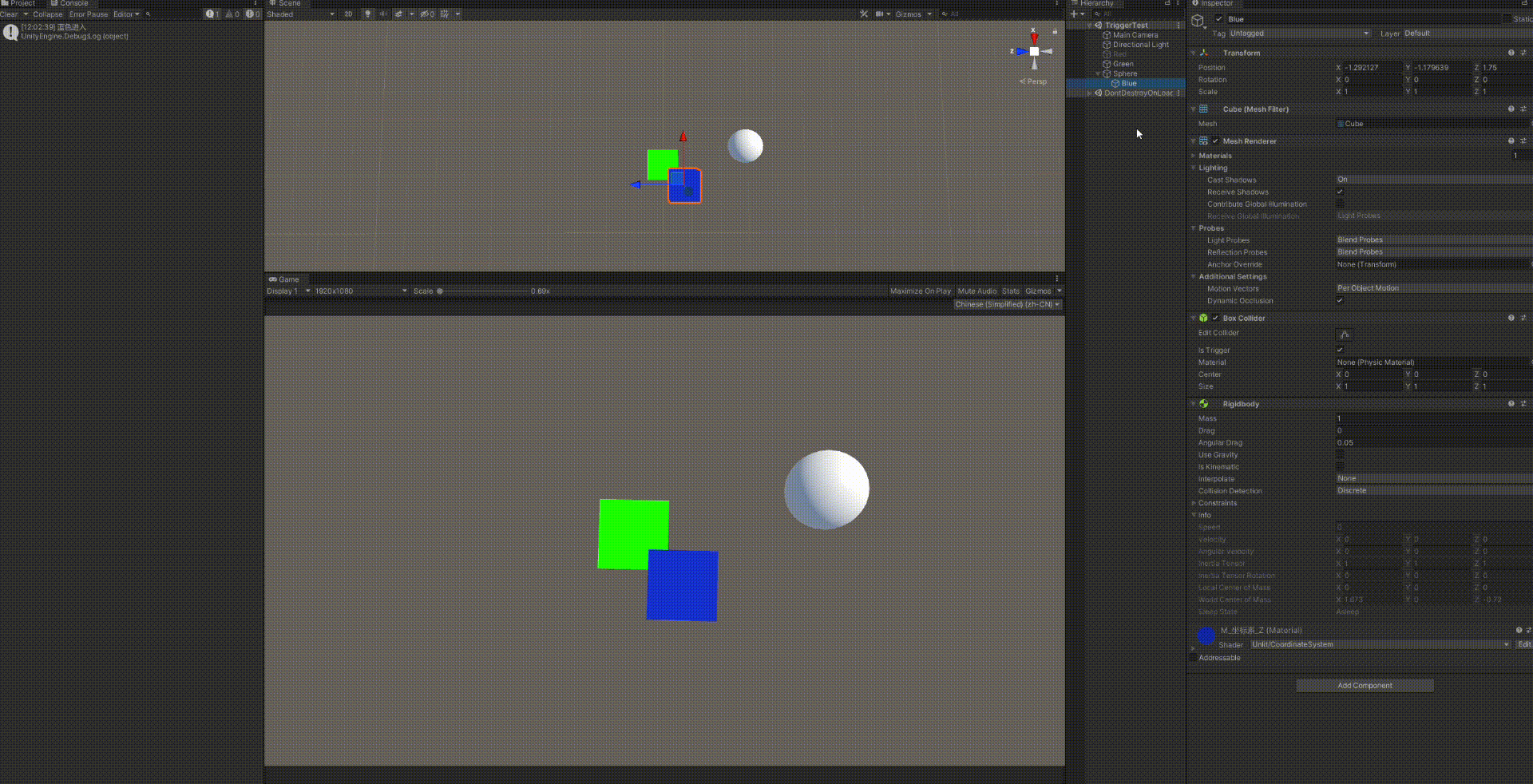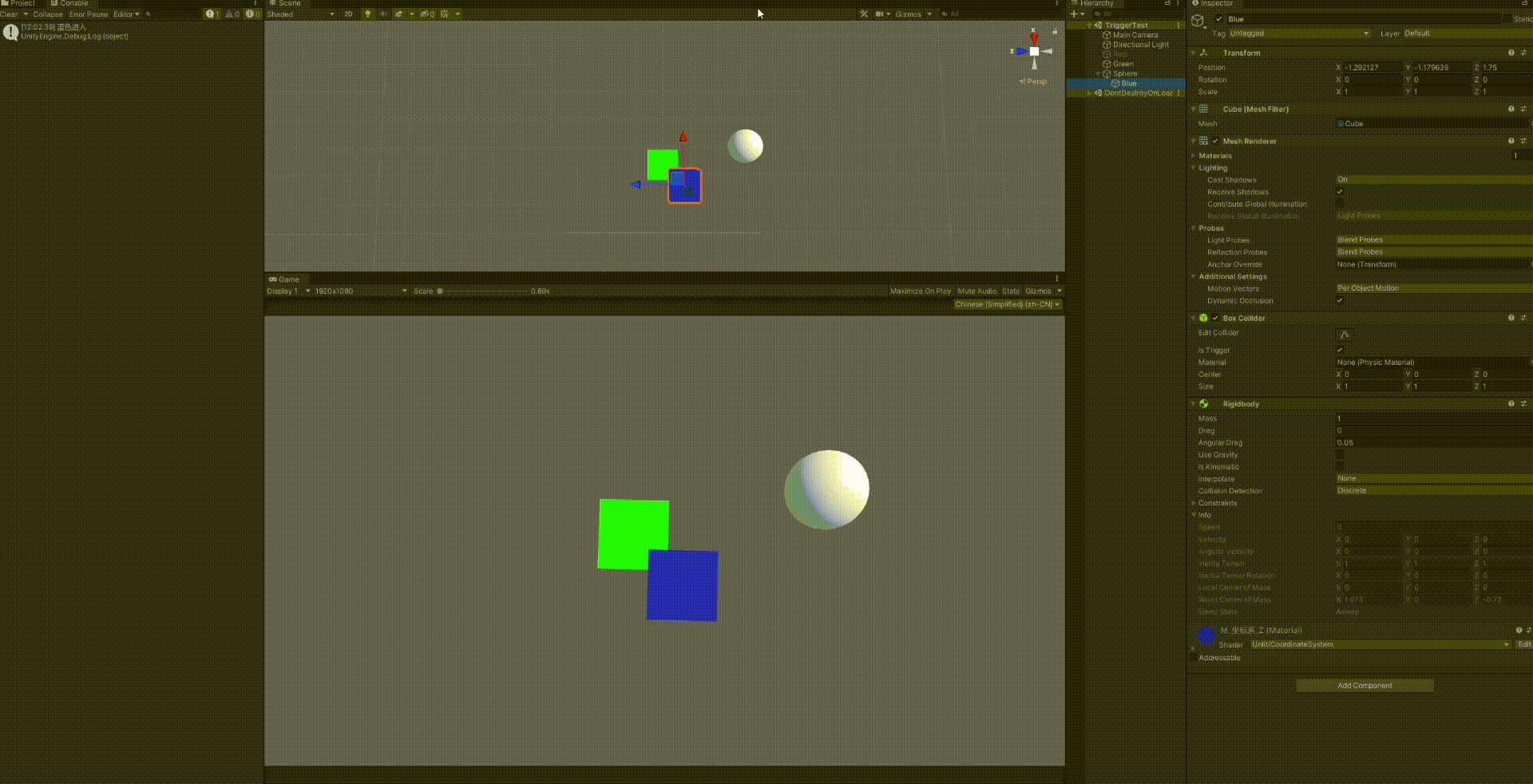
然后我将蓝色方块的父物体设置为白色小球,会触发蓝色小球进入

假如说蓝色没有碰撞盒,则不管怎么设置父物体都不会触发任何操作
踩坑4
红色方块:刚体+碰撞盒
绿色方块:刚体+碰撞盒+检测触发碰撞脚本
蓝色方块:碰撞盒
蓝色方块的父物体是红色方块,红色方块和绿色方块都接触绿色小球
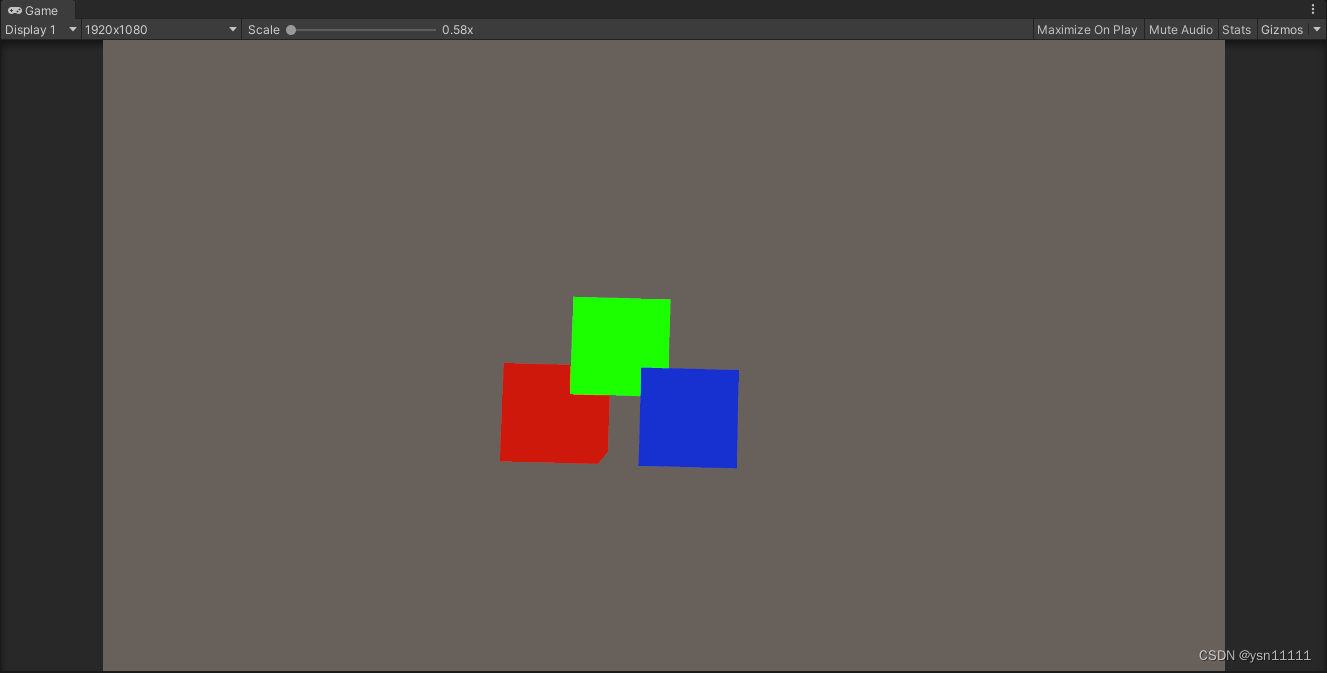
然后我点击红色方块刚体上的Is Kinematic,或者取消点击红色方块的Is Kinematic

在此基础上 还是保持蓝色方块的父物体上红色方块 给蓝色方块添加刚体,我再去切换红色方块刚体上的Is Kinematic

结论:刚体会起到一个隔断作用,它管理的是本体加所有不带刚体的子物体,如果有出现带刚体的子物体A,将不会触发A和A的子物体的物理检测。







![[ECE] Error Codes: Parity Bit and Cyclic Redundancy Check](http://pic.xiahunao.cn/[ECE] Error Codes: Parity Bit and Cyclic Redundancy Check)
)




。Javaee项目,springboot vue前后端分离项目)



)


六个默认成员函数)