输入一个包含 n
个方程 n
个未知数的异或线性方程组。
方程组中的系数和常数为 0
或 1
，每个未知数的取值也为 0
或 1
。
求解这个方程组。
异或线性方程组示例如下：
M[1][1]x[1] ^ M[1][2]x[2] ^ … ^ M[1][n]x[n] = B[1]
M[2][1]x[1] ^ M[2][2]x[2] ^ … ^ M[2][n]x[n] = B[2]
…
M[n][1]x[1] ^ M[n][2]x[2] ^ … ^ M[n][n]x[n] = B[n]
其中 ^ 表示异或(XOR
)，M[i][j]
表示第 i
个式子中 x[j]
的系数，B[i]
是第 i
个方程右端的常数，取值均为 0
或 1
。
输入格式
第一行包含整数 n
。
接下来 n
行，每行包含 n+1
个整数 0
或 1
，表示一个方程的 n
个系数以及等号右侧的常数。
输出格式
如果给定线性方程组存在唯一解，则输出共 n
行，其中第 i
行输出第 i
个未知数的解。
如果给定线性方程组存在多组解，则输出 Multiple sets of solutions。
如果给定线性方程组无解，则输出 No solution。
数据范围
1≤n≤100
输入样例：
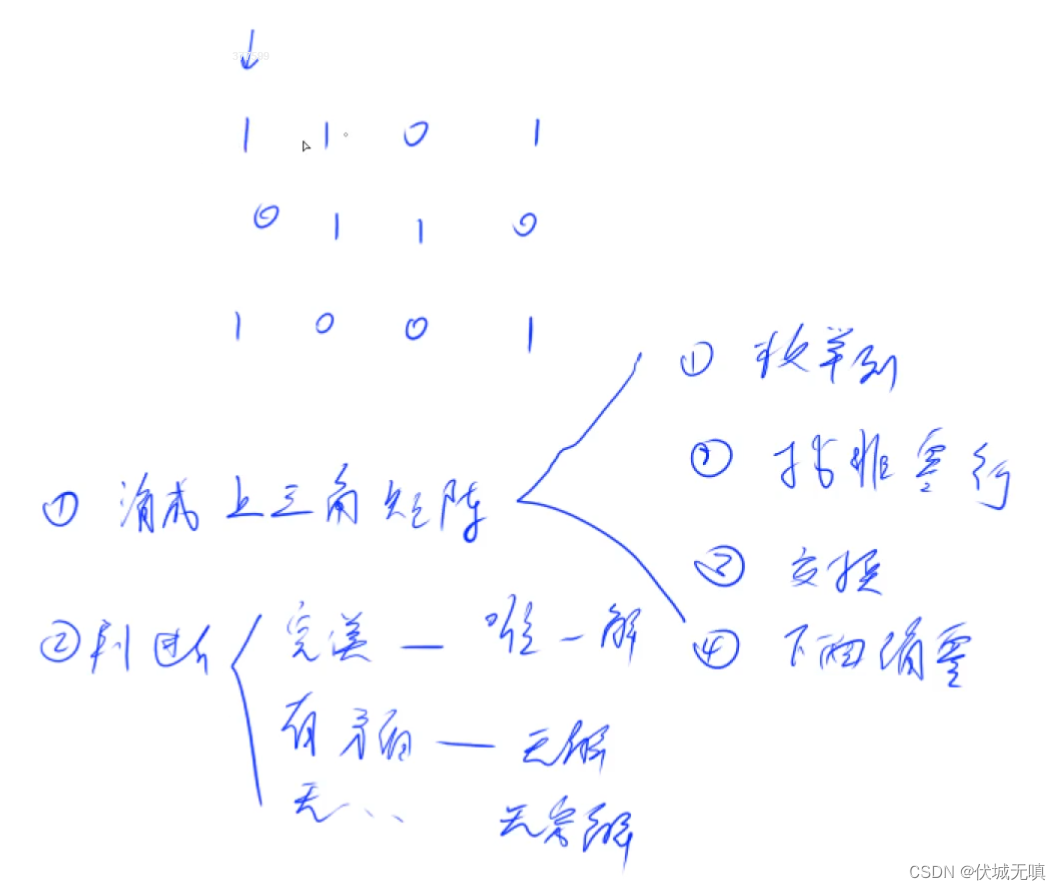
3
1 1 0 1
0 1 1 0
1 0 0 1
输出样例：
1
0
0
#include <iostream>
#include <algorithm>using namespace std;const int N = 110;int n;
int a[N][N];int xor_gauss()
{int c, r;for(c = 0, r = 0; c < n; c ++ ){int t = r;for(int i = r; i < n; i ++ )if(a[i][c]) //找到第一个非零行就行{t = i;break;}if(!a[t][c]) //往下找完发现并不存在一个非零的，这列就结束了continue;for(int i = c; i <= n; i ++ ) swap(a[t][i], a[r][i]);for(int i = r + 1; i < n; i ++ )if(a[i][c]) //如果不为0，才消去for(int j = n; j >= c; j -- )a[i][j] = a[i][j] ^ a[r][j];r ++; }if(r < n){for(int i = r; i < n; i ++ ) //判断是否有矛盾，现在i行左边是全部为0的，右边不为0，出现矛盾if(a[i][n])return 0; //无解return 2; // 无穷组解}for(int i = n - 1; i >= 0; i -- ) //回带求解for(int j = i + 1; j < n; j ++ )a[i][n] = a[i][n] ^ a[i][j] & a[j][n]; //a[j][n] 此时就是xj的值return 1; //唯一解
}int main ()
{cin>>n;for(int i = 0; i < n; i ++ )for(int j = 0; j <= n; j ++ )cin>>a[i][j];int res = xor_gauss();if(res == 1) for(int i = 0; i < n; i ++ )cout<<a[i][n]<<endl;else if(res == 2)cout<<"Multiple sets of solutions"<<endl;elsecout<<"No solution"<<endl;return 0;}
