matlab中提供了小波变换函数lwt和ilwt,可以方便地实现提升小波变换。
我们按照小波变换的定义,粗糙地实现一个针对图像的小波变换,如下:
% 使用方法:
img = imread('lena256.bmp'); % 假设lena.png是灰度图像
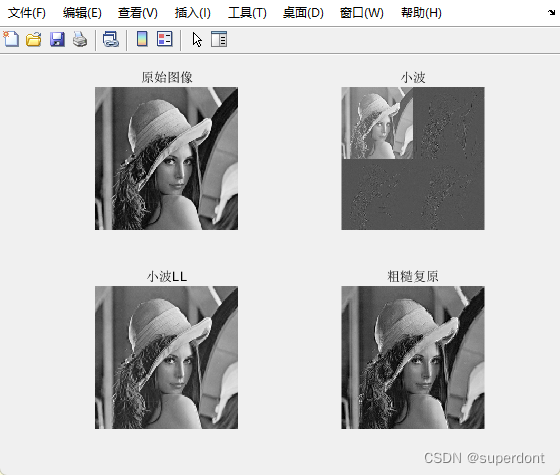
subplot(2,2,1),imshow(img,[]);title('原始图像');
[m,n]=size(img);
result = wavelet_transform(img);
subplot(2,2,2),imshow(result,[]);title('小波');
subplot(2,2,3),imshow(result(1:m/2,1:n/2),[]);title('小波LL');
image = inverse_wavelet_transform(result);
subplot(2,2,4),imshow(image,[]);title('粗糙复原');function temp = wavelet_transform(image)
% 对输入图像进行一次5/3小波变换
% image: 输入的灰度图像
% LL, LH, HL, HH: 分解得到的四个子带图像
% 预处理 - 将图像转为double类型
image = double(image);% 水平方向提升小波变换
[rows, cols] = size(image);
temp = zeros(size(image)); % 用于存储水平方向处理后的临时结果
for i = 1:rows[sL, dL] = lifting_scheme(image(i, :));temp(i, 1:end/2) = sL; % 放在前面temp(i, end/2+1:end) = dL; % 放在后面
end% 垂直方向提升小波变换
for j = 1:cols[sL, dL] = lifting_scheme(temp(:, j)');temp(1:end/2,j) = sL; %放前面temp(end/2+1:end,j) = dL; %放后面
endendfunction [s, d] = lifting_scheme(x)
% 提升小波分解
% 输入序列 x 应为偶数长度
% 输出 s 为近似系数序列,d 为细节系数序列% 分裂步骤
e = x(1:2:end);
o = x(2:2:end);% 预测步骤
p = (e + [e(2:end), e(end)]) / 2; % 使用边界延拓对最后一个元素进行处理
d = o - p; % 计算细节系数% 更新步骤
u = (d + [d(2:end), d(end)]) / 4; % 类似地处理最后一个元素
s = e + u; % 更新近似系数
endfunction image = inverse_wavelet_transform(temp)
% 对输入的小波变换结果进行逆变换
% temp: 小波变换的结果
% image: 重建后的灰度图像% 先进行垂直方向的逆变换
[rows, cols] = size(temp);
image = zeros(size(temp)); % 用于存储垂直方向处理后的临时结果
for j = 1:colssL = temp(1:end/2, j)';dL = temp(end/2+1:end, j)';image(:, j) = inverse_lifting_scheme(sL, dL);
end% 再进行水平方向的逆变换
for i = 1:rowssL = image(i, 1:end/2);dL = image(i, end/2+1:end);image(i, :) = inverse_lifting_scheme(sL, dL);
end% 后处理 - 将图像转为uint8类型(如果需要)
image = uint8(image);endfunction x = inverse_lifting_scheme(s, d)
% 提升小波重建
% s: 近似系数序列
% d: 细节系数序列
% x: 重建后的序列% 逆更新步骤
u = (d + [d(2:end), d(1)]) / 4; % 注意这里首尾相接的方式不同于上面
e = s - u;% 逆预测步骤
p = (e + [e(1), e(1:end-1)]) / 2; % 同理,这里使用的也是不同的边界延拓方式
o = d + p;% 合并步骤
x(1:2:length(e)*2) = e;
x(2:2:length(o)*2) = o;end%% 下面的代码进行图像本身的拓边,保证在预测、更新过程中能被除尽
% % 检查 e 和 o 的长度,确保它们匹配
% if length(e) > length(o)
% % 如果 e 的长度比 o 长,则需要扩展 o
% o(end+1) = 2 * o(end) - e(end); % 可以是其他边界扩展策略
% end%% 下面的代码涉及到边界拓展模式,可以作为参考。% function [s, d] = lifting_scheme(x)
% % 提升小波分解
% % 输入序列 x 应为偶数长度
% % 输出 s 为近似系数序列,d 为细节系数序列
%
% % 分裂步骤
% e = x(1:2:end);
% o = x(2:2:end);
%
% % 预测步骤
% p = zeros(1, length(o));
% p(1) = e(1); % 对于序列的首端,直接取值(或使用其他边界延拓策略)
% p(2:end) = (e(1:end-1) + e(2:end)) / 2; % 平均相邻的e值进行预测
% d = o - floor(p);
%
% % 更新步骤
% u = zeros(1, length(e));
% % u(1:end-1) = (d(1:end-1) + [d(2:end), 0]) / 4; % 更新e值,除最后一个d外
% u(1:end-1) = (d(1:end-1) + d(2:end)) / 4; % 更新e值,除最后一个d外
% u(end) = (d(end) + d(end-1)) / 4; % 最后一个e值的更新
% s = e + floor(u);
% end% function [s, d] = lifting_scheme(x)
% % 提升小波分解
% % 输入序列 x 应为偶数长度
% % 输出 s 为近似系数序列,d 为细节系数序列
%
% % 分裂步骤
% e = x(1:2:end);
% o = x(2:2:end);
%
% % % 预测步骤
% % p = [e(1); (e(1:end-1) + e(2:end)) / 2]; % 对于序列的首端,使用边界延拓
% % d = o - floor(p);
% %
% % % 更新步骤
% % u = [(d(1) + d(2)) / 4; (d(1:end-1) + d(2:end)) / 4];
% % s = e + floor(u);
%
% % 预测步骤
% % 对于序列的首端和末端,使用边界延拓
% p = [(e(1) + e(2)) / 2; (e(1:end-1) + e(2:end)) / 2; (e(end-1) + e(end)) / 2];
% p = p(1:length(o)); % 使 p 和 o 长度一致
% d = o - floor(p);
%
% % 更新步骤
% u = [(d(1) + d(2)) / 4; (d(1:end-1) + d(2:end)) / 4; (d(end) + d(end-1)) / 4];
% u = u(1:length(e)); % 使 u 和 e 长度一致
% s = e + floor(u);
% end
运行结果如下:


2024.01.27)



控制)








)



