💥💥💞💞欢迎来到本博客❤️❤️💥💥
🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。
⛳️座右铭:行百里者,半于九十。
📋📋📋本文目录如下:🎁🎁🎁
目录
💥1 概述
📚2 运行结果
🎉3 参考文献
🌈4 Matlab代码实现
💥1 概述
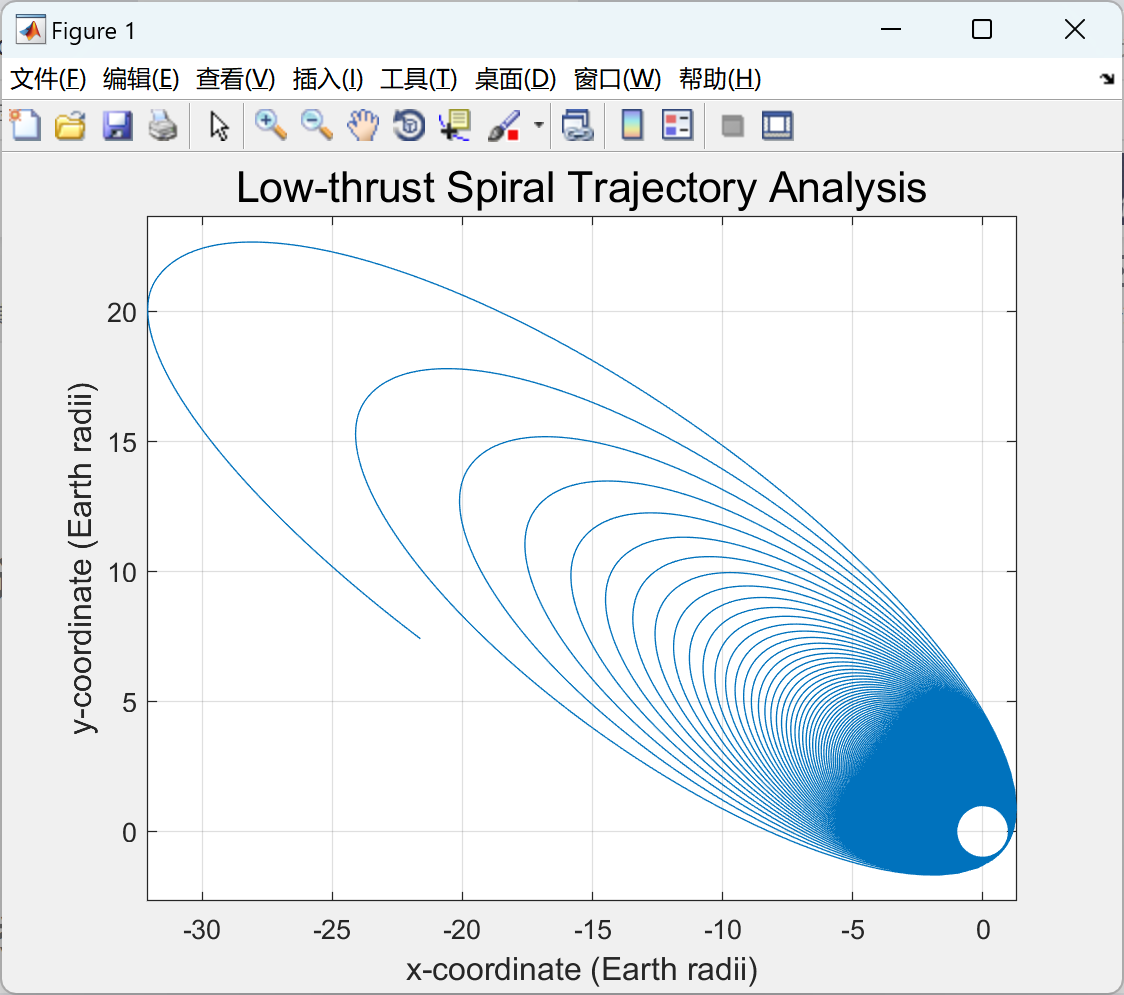
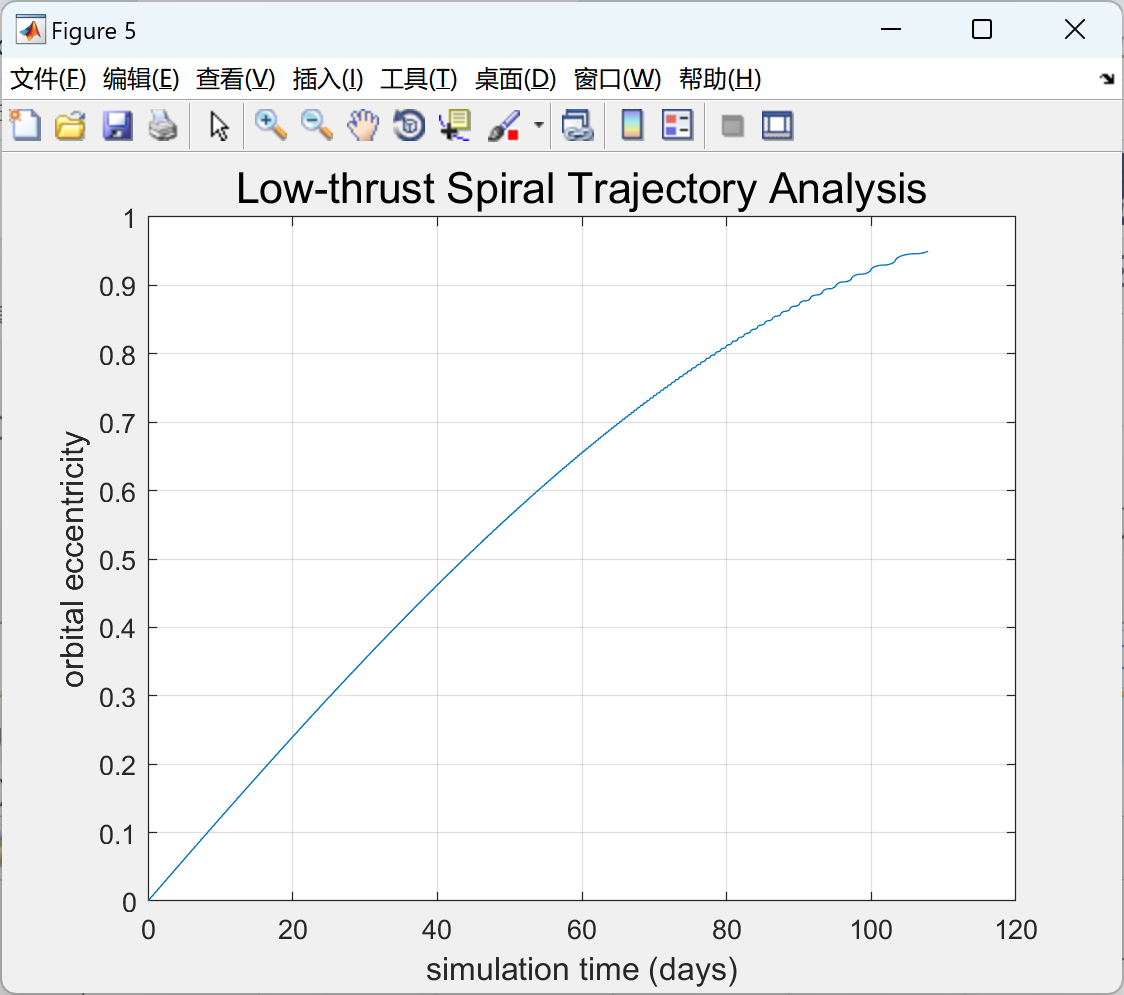
本文可用于设计和分析具有恒定近心点半径的低推力螺旋轨迹。低推力轨迹设计是一种航天器轨道设计的方法,通过使用较小的推力在较长的时间内进行轨道转移,以实现目标轨道的变化。这种方法适用于需要节省燃料或对轨道精度要求较高的任务。
用户需要提供初始地球停泊轨道的经典轨道要素,这些要素包括轨道倾角、升交点赤经、近地点幅角、轨道倾角的变化率以及近地点幅角的变化率。此外,用户还需要提供最终或“目标”轨道的离心率,即目标轨道的形状。
航天器的轨道运动是使用修改的赤道坐标轨道要素进行建模。这些修改的赤道坐标轨道要素包括半长轴、离心率、倾角、升交点赤经和近地点幅角。通过使用这些轨道要素,可以准确地描述航天器在轨道上的位置和速度。
在进行轨道转移计算时,本脚本假设整个轨道转移过程中推力加速度是恒定的。这意味着航天器在整个轨道转移过程中以相同的推力加速度进行运动。这种简化假设可以简化计算过程,并得到近似的轨道解决方案。
此外,本脚本还假设轨道运动是开普勒运动或未受扰动的。这意味着在计算过程中不考虑其他天体或外力对航天器轨道的影响。这种假设适用于大多数低地球轨道任务,其中其他天体或外力的影响可以忽略不计。
可以设计和分析具有恒定近地点半径的低推力螺旋轨道,以满足特定任务的要求。这个代码提供了一个简单而有效的工具,可以帮助工程师和科学家在航天器轨道设计和分析方面取得更好的结果。
📚2 运行结果



部分代码:
function [r, v, smovrp, cosl, sinl, wmee, ssqrd] = mee2eci_lts(mu, mee)
% convert modified equinoctial orbital elements to eci position
% and velocity vectors and auxillary variables
% input
% mu = gravitational constant (km**3/sec**2)
% mee(1) = semilatus rectum of orbit (kilometers)
% mee(2) = f equinoctial element
% mee(3) = g equinoctial element
% mee(4) = h equinoctial element
% mee(5) = k equinoctial element
% mee(6) = true longitude (radians)
% output
% r = eci position vector (kilometers)
% v = eci velocity vector (kilometers/second)
% auxilliary output quantities
% smovrp = sqrt(mu / pmee)
% cosl = cos(xlmee)
% sinl = sin(xlmee)
% wmee = 1.0 + fmee * cosl + gmee * sinl
% ssqrd = 1.0 + tani2s
% Orbital Mechanics with Matlab
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% unload equinoctial orbital elements
pmee = mee(1);
fmee = mee(2);
gmee = mee(3);
hmee = mee(4);
xkmee = mee(5);
xlmee = mee(6);
smovrp = sqrt(mu / pmee);
tani2s = hmee^2 + xkmee^2;
cosl = cos(xlmee);
sinl = sin(xlmee);
wmee = 1.0 + fmee * cosl + gmee * sinl;
radius = pmee / wmee;
hsmks = hmee^2 - xkmee^2;
ssqrd = 1.0 + tani2s;
% compute eci position vector (kilometers)
🎉3 参考文献
文章中一些内容引自网络,会注明出处或引用为参考文献,难免有未尽之处,如有不妥,请随时联系删除。
[1]刘玥.火星探测器近心点制动与轨道保持优化设计[D].哈尔滨工业大学,2011.DOI:10.7666/d.D262275.
[2]夏勇俊.具有中心导体轴的螺旋槽慢波系统及注—波互作用的研究[D].电子科技大学[2023-08-27].DOI:CNKI:CDMD:2.2002.102390.

)



)

远程开发golang、python环境安装)






)

检测原图片类型?)
)


)