1 埃里克·坦普尔·贝尔

贝尔数是组合数学中的一组整数数列,以埃里克·坦普尔·贝尔(Eric Temple Bell)命名,
埃里克·坦普尔·贝尔(生于1883年2月7日,苏格兰阿伯丁郡阿伯丁,于1960年12月21日在美国加利福尼亚州沃特森维尔去世),苏格兰裔美国数学家、教育家和作家,对分析数论做出了重大贡献。
贝尔在19岁时移民到美国,并立即进入斯坦福大学就读,两年后他在那里获得了学士学位。经过1908年的努力,他获得了华盛顿大学的硕士学位。同样,在又一年的预科之后,他于1912年从哥伦比亚大学获得了数学博士学位。在这几年之间,贝尔结婚了,尝试做骡子剥皮工、牧场工人、测量员、教师和其他行业的工作。贝尔在获得博士学位后立即接受了华盛顿大学教学数学的职位,他一直担任该校的数学教授,直到1926岁才被任命为加州理工大学数学教授。从1931年到1933年,他担任美国数学协会主席。
贝尔发表了大约250篇学术文章。因其作品《算术释义》(1921年),他于1924年获得Bôcher奖。他的两本书《代数算术》(1927年)和《数学的发展》(1940年)成为该领域的标准,后者用清晰、简洁的语言概述了贝尔认为最重要的数学趋势。
贝尔最为人所知的是他的畅销书,如《数学人》(1937)和《数学女王与科学仆人》(1951)。他还写了费马最后一个定理,最后一个问题(1961年)的历史。这些作品,尤其是数学方面的作品,尽管相当离奇,也不总是历史上准确的,但仍然吸引着广泛的读者。贝尔以约翰·泰恩的笔名写了许多科幻小说,包括《时间流》(1946年)。
2 计算方法与源程序
Bell数的定义:第n个Bell数表示集合{1,2,3,...,n}的划分方案数,即:B[0] = 1;
每一个Bell数都是第二类Stirling数的和,即:
第二类Stirling数的意义是:S(n,k)表示将n个物体划分成k个非空的不可辨别的(可以理解为盒子没有编号)集合的方法
数。很明显,每一个Bell是对应的第二类Stirling数之和。

3 源代码
3.1 文本格式
using System;
using System.Text;
using System.Collections;
using System.Collections.Generic;
namespace Legalsoft.Truffer.Algorithm
{
public static partial class Number_Sequence
{
/// <summary>
/// 贝尔数(Bell Number)的计算方法
/// </summary>
/// <param name="n"></param>
/// <returns></returns>
public static long Bell_Number(int n)
{
long[,] bell = new long[n + 1, n + 1];
bell[0, 0] = 1;
for (int i = 1; i <= n; i++)
{
bell[i, 0] = bell[i - 1, i - 1];
for (int j = 1; j <= i; j++)
{
bell[i, j] = bell[i - 1, j - 1] + bell[i, j - 1];
}
}
return bell[n, 0];
}
}
}
3.2 代码格式
using System;
using System.Text;
using System.Collections;
using System.Collections.Generic;namespace Legalsoft.Truffer.Algorithm
{public static partial class Number_Sequence{/// <summary>/// 贝尔数(Bell Number)的计算方法/// </summary>/// <param name="n"></param>/// <returns></returns>public static long Bell_Number(int n){long[,] bell = new long[n + 1, n + 1];bell[0, 0] = 1;for (int i = 1; i <= n; i++){bell[i, 0] = bell[i - 1, i - 1];for (int j = 1; j <= i; j++){bell[i, j] = bell[i - 1, j - 1] + bell[i, j - 1];}}return bell[n, 0];}}
}
————————————————————————
POWER BY TRUFFER.CN
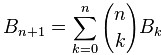
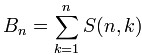
——思路、程序总结分享)
)

——“C++”)





)
)








)