目录
概念解释
栈
队列
树
树的概念
结点的分类
有序树
无序树
森林
二叉树
满二叉树
完全二叉树
二叉排序树
平衡二叉树
1.用栈实现队列
解法:双栈
2.字符串解码
解法:栈
3.二叉树的中序遍历
解法一:递归
解法二:迭代
4.二叉树的前序遍历
解法一:递归
解法二:迭代
5.二叉树的后序遍历
6.平衡二叉树
自底向上的递归
7.二叉树的最大深度
解法一:迭代
解法二:递归
8.对称二叉树
解法一:递归
解法二:迭代
概念解释
栈
栈(堆栈) : 后进先出的结构,Last In First Out,简称LIFO结构。
队列
先进先出的结构,First In First Out,简称FIFO结构。
树
树(Tree)是n(n >= 0)个结点的有限集合,当n=0时,称为空树。
在任意一个非空树中应满足:
1.有且仅有一个特定的称为根(Root)的结点。
2.当n>1时,其余节点可分成m(m>0)个互不相交的有限集合T1,T2,...Tm,其中每个集合本身又是一棵树,并且称为根结点的子树(SubTree)。
树的概念
结点的度:结点拥有的子树的数量;
结点的深度(层次):从上往下数,结点距离根结点的距离。
结点的高度:从下往上数,结点在第几层,结点的高度就是多少;
树的高度:结点深度最大的那个结点的深度就是树的深度;
树的度:树中度最大结点的度就是树的度。
结点的分类
叶子节点:度为0的结点;
分支结点(内部结点):度不为0的结点(除根节点)。
有序树
从逻辑上看,树中结点的各子树从左至右是有次序的,不能互换。

无序树
从逻辑上看,树中结点的各子树从左至右是无次序的,可以互换。
森林
m(m>=0)棵互不相交的树的集合。

二叉树
二叉树是n(n>=0)个结点的有限集合;
可以是空二叉树,即n=0;
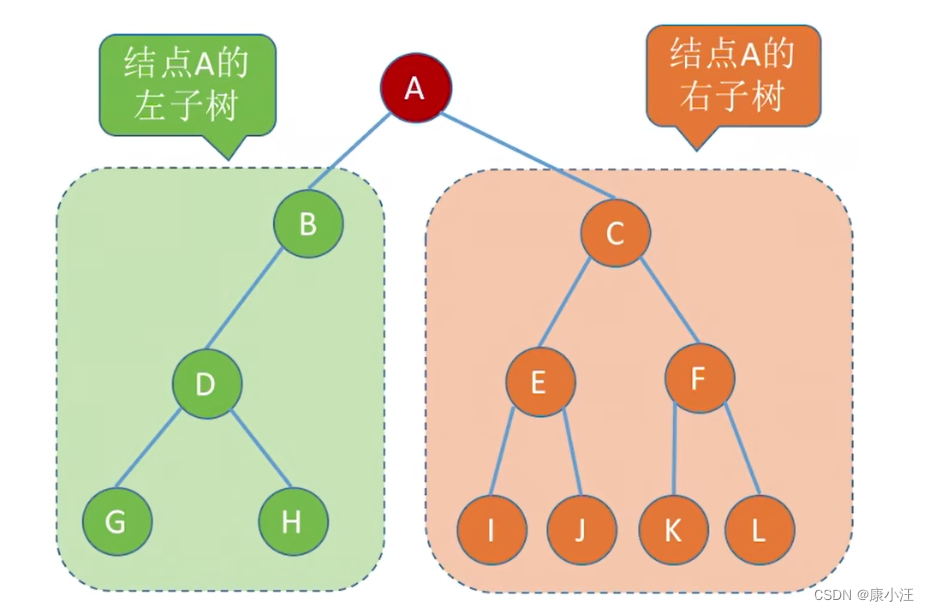
可以是由一个根节点和两个互不相交的树(被称为根的左子树和右子树)组成。
左子树和右子树又分别是一课二叉树。、
特点:每个结点最多只有两棵子树;
左右子树不能颠倒(二叉树是有序树)
满二叉树
每层结点的个数都达到最大值;即如果一个二叉树的层数为k,并且总结点数位
-1,那么这个数就是满二叉树。
特点:1.最后一层都是叶子节点;
2.不存在度为1的结点;
3.按层序从1开始编号,结点i的左孩子为2i,右孩子为2i+1;
结点i的父结点为i/2向下取整。

完全二叉树
当且仅当其每个结点都与满二叉树中编号位1-n的结点一一对应时,称为完全二叉树。
即,相比于满二叉树,完全二叉树少一个右下角。
特点:1.只有最后两层可能又叶子结点;
2.最多只有一个度为1的结点;
3.按层序从1开始编号,结点i的左孩子为2i,右孩子为2i+1;
结点i的父结点为i/2向下取整。
4.如果一个完全二叉树的有n个结点,那么,当结点的编号i<=n/2向下取整,那么这些结点为分支结点;当结点的编号i>n/2向下取整,那么这些结点为叶子结点;

二叉排序树
左子树上所有结点的关键字均小于根节点的关键字,右子树上所有结点的关键字均大于根节点的关键字;左子树和右子树又各是一棵二叉排序树。

平衡二叉树
树上任一结点的左子树和右子树的深度之差不超过1.

1.用栈实现队列
请你仅使用两个栈实现先入先出队列。队列应当支持一般队列支持的所有操作(push、pop、peek、empty):
实现 MyQueue 类:
void push(int x)将元素 x 推到队列的末尾int pop()从队列的开头移除并返回元素int peek()返回队列开头的元素boolean empty()如果队列为空,返回true;否则,返回false
说明:
- 你 只能 使用标准的栈操作 —— 也就是只有
push to top,peek/pop from top,size, 和is empty操作是合法的。 - 你所使用的语言也许不支持栈。你可以使用 list 或者 deque(双端队列)来模拟一个栈,只要是标准的栈操作即可

进阶:
- 你能否实现每个操作均摊时间复杂度为
O(1)的队列?换句话说,执行n个操作的总时间复杂度为O(n),即使其中一个操作可能花费较长时间。
解法:双栈
利用双栈就可以实现队列,一个做输入栈,一个做输出栈。
队列是先进先出,栈刚好相反,但如果,先把数据压入输入栈,再从输入栈将数据压入输出栈,就和队列一样了。
class MyQueue {private static Stack<Integer> inStack;private static Stack<Integer> outStack;public MyQueue() {inStack = new Stack<Integer>();outStack = new Stack<Integer>();}public void push(int x) {inStack.push(x);}public int pop() {if(outStack.isEmpty()){inToOut();}return outStack.pop();}private void inToOut(){//如果输入栈非空,将输入栈的元素弹出,然后压入输出栈while(!inStack.isEmpty()){outStack.push(inStack.pop());}}public int peek() {if(outStack.isEmpty()){inToOut();}return outStack.peek();}public boolean empty() {return inStack.isEmpty() && outStack.isEmpty();}
}/*** Your MyQueue object will be instantiated and called as such:* MyQueue obj = new MyQueue();* obj.push(x);* int param_2 = obj.pop();* int param_3 = obj.peek();* boolean param_4 = obj.empty();*/
2.字符串解码
给定一个经过编码的字符串,返回它解码后的字符串。
编码规则为: k[encoded_string],表示其中方括号内部的 encoded_string 正好重复 k 次。注意 k 保证为正整数。
你可以认为输入字符串总是有效的;输入字符串中没有额外的空格,且输入的方括号总是符合格式要求的。
此外,你可以认为原始数据不包含数字,所有的数字只表示重复的次数 k ,例如不会出现像 3a 或 2[4] 的输入。

解法:栈
本题考查我们对栈的操作。
以3[a]2[bc]为例,我们从3开始入栈;
如果是数字,将数字进行解析,然后进栈,
如果是 [ 或者 字母,直接进栈,
如果是 ] ,开始出栈,直到遇到 [ 为止。
class Solution {public String decodeString(String s) {//存数字的栈Stack<Integer> countStack = new Stack<>();//存字母或 [ ] 的栈Stack<String> resStack = new Stack<>();//初始下标int index = 0;int len = s.length();String res = "";while(index < len){char ch = s.charAt(index);//处理数字if(Character.isDigit(ch)){StringBuffer sb = new StringBuffer();//如果是数字,就加到sb中while(Character.isDigit(s.charAt(index))){sb.append(s.charAt(index++));}countStack.push(Integer.parseInt(sb.toString()));}else if(ch == '['){//当ch为[ 时,让res入栈,将res置空resStack.push(res);res = "";index++;}else if(ch == ']'){//当ch为]时,开始出栈StringBuffer temp = new StringBuffer(resStack.pop());int repeaTims = countStack.pop();for(int i = 0;i<repeaTims;i++){temp.append(res);}res = temp.toString();index++;}else{//当ch为字母时,拼接到res后面res += s.charAt(index++);}}return res;}
}3.二叉树的中序遍历
给定一个二叉树的根节点 root ,返回 它的 中序 遍历 。
进阶: 递归算法很简单,你可以通过迭代算法完成吗?

解法一:递归
首先,我们要知道二叉树的中序遍历是什么,根节点-左子树-右子树,而且在访问左子树或右子树时,还是同样的方式,直到整个树遍历完,终止条件就是当结点为空时,中止。
/*** Definition for a binary tree node.* public class TreeNode {* int val;* TreeNode left;* TreeNode right;* TreeNode() {}* TreeNode(int val) { this.val = val; }* TreeNode(int val, TreeNode left, TreeNode right) {* this.val = val;* this.left = left;* this.right = right;* }* }*/
class Solution {public List<Integer> inorderTraversal(TreeNode root) {List<Integer> res = new ArrayList<>();accessTree(root,res);return res;}public void accessTree(TreeNode root,List<Integer> res){if(root == null){return;}accessTree(root.left,res);res.add(root.val);accessTree(root.right,res);}
}
时间复杂度:O(n)
空间复杂度:O(n)
解法二:迭代
题目要求使用迭代。
首先,我们要明确中序遍历的步骤:左、根、右;所以先访问左子树,但是根节点的值需要保存下来,因为我们为了效率,必须保证每个结点只访问了一次。
我们引入一个栈用来保存根节点。
迭代步骤:先将根节点压入栈,然后访问左子树,如果左子树不为空,继续将左子树的根节点压入栈,如果左子树为空,将其弹出栈然后输出,在访问右子树,直到整个树遍历完。
public List<Integer> inorderTraversal(TreeNode root) {List<Integer> res = new ArrayList<>();Stack<TreeNode> stack = new Stack<>();while(root != null || !stack.isEmpty()){while(root!=null){stack.push(root);root = root.left;}root = stack.pop();res.add(root.val);root = root.right;}return res;}
时间复杂度:O(n)
空间复杂度:O(n)
4.二叉树的前序遍历
给你二叉树的根节点 root ,返回它节点值的 前序 遍历。
和中序遍历思路一样。
要注意的是遍历顺序:根节点、左子树、右子树
解法一:递归
public List<Integer> preorderTraversal(TreeNode root) {List<Integer> res = new ArrayList<>();accessTree(root,res);return res;}public void accessTree(TreeNode root,List<Integer> res){//终止条件if(root==null){return;}//先访问根节点res.add(root.val);//左子树accessTree(root.left,res);//右子树accessTree(root.right,res);} 时间复杂度:O(n)
时间复杂度:O(n)
空间复杂度:O(n)
解法二:迭代
public List<Integer> preorderTraversal(TreeNode root) {List<Integer> res = new ArrayList<>();Stack<TreeNode> stack = new Stack<>();while(root!=null || !stack.isEmpty()){while(root!=null){res.add(root.val);stack.push(root);root = root.left;}root = stack.pop();root = root.right;}return res;}
时间复杂度:O(n)
空间复杂度:O(n)
5.二叉树的后序遍历
给你一棵二叉树的根节点 root ,返回其节点值的 后序遍历 。
进阶:递归算法很简单,你可以通过迭代算法完成吗?
递归跟前两个思路一样,但是迭代就差很多,这是因为后序遍历的步骤是左子树、右子树、根节点,每次需要遍历右子树时,都需要借助根结点,所以这里需要定义一个空结点,每次都要保存根节点。
class Solution {public List<Integer> postorderTraversal(TreeNode root) {List<Integer> res = new ArrayList<Integer>();if (root == null) {return res;}Deque<TreeNode> stack = new LinkedList<TreeNode>();TreeNode prev = null;while (root != null || !stack.isEmpty()) {while (root != null) {stack.push(root);root = root.left;}root = stack.pop();if (root.right == null || root.right == prev) {res.add(root.val);prev = root;root = null;} else {stack.push(root);root = root.right;}}return res;}
}6.平衡二叉树
给定一个二叉树,判断它是否是高度平衡的二叉树。
本题中,一棵高度平衡二叉树定义为:
一个二叉树每个节点 的左右两个子树的高度差的绝对值不超过 1 。
自底向上的递归
public boolean isBalanced(TreeNode root) {return height(root) != -1;}public int height(TreeNode root){if(root == null){return 0;}//从左子树开始判断int leftH = height(root.left);int rightH = height(root.right);if(leftH == -1 || rightH == -1 || (leftH-rightH) > 1||(rightH-leftH)>1){return -1;}return leftH > rightH ? (leftH + 1):(rightH + 1);}
7.二叉树的最大深度
给定一个二叉树 root ,返回其最大深度。
二叉树的 最大深度 是指从根节点到最远叶子节点的最长路径上的节点数。
解法一:迭代
使用队列里存放当前层的所有节点。每次拓展下一层的时候,我们需要将队列里的所有节点都拿出来进行拓展,这样能保证每次拓展完的时候队列里存放的是当前层的所有节点,即我们是一层一层地进行拓展,最后我们用一个变量 ans\textit{ans}ans 来维护拓展的次数,
public int maxDepth(TreeNode root) {if(root == null){return 0;}Queue<TreeNode> q = new LinkedList<>();int count = 0;q.offer(root);while(!q.isEmpty()){int size = q.size();while(size>0){TreeNode n = q.poll();if(n.left != null){q.offer(n.left);}if(n.right!=null){q.offer(n.right);}size--;}count++;}return count;}
解法二:递归
如果我们知道了左子树和右子树的最大深度 l和 r,那么该二叉树的最大深度即为
max(l,r)+1.
而左子树和右子树的最大深度又可以以同样的方式进行计算。
public int maxDepth(TreeNode root) {if(root == null){return 0;}int l = maxDepth(root.left);int r = maxDepth(root.right);return l > r ? l + 1 : r +1;}
8.对称二叉树
给你一个二叉树的根节点 root , 检查它是否轴对称。
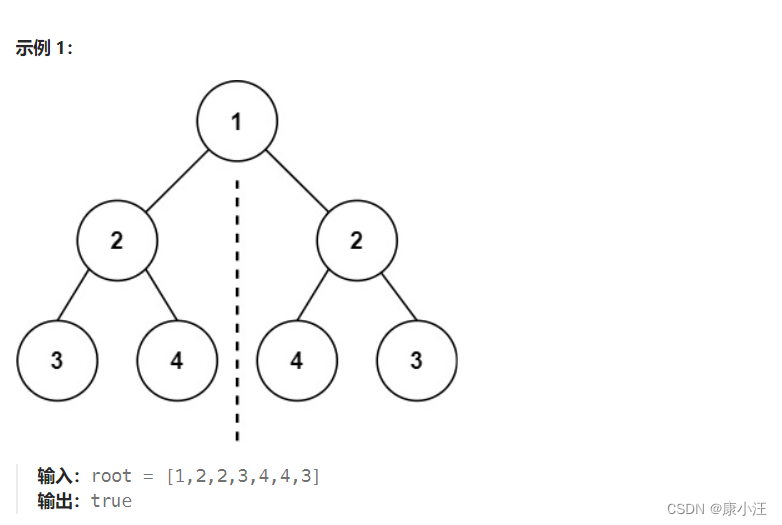
解法一:递归
乍一看使用递归很好解决。
根据题目的描述,镜像对称,就是左右两边相等,也就是左子树和右子树是相当的。
注意这句话,左子树和右子相等,也就是说要递归的比较左子树和右子树。
class Solution {public boolean isSymmetric(TreeNode root) {if(root==null) {return true;}return dfs(root.left,root.right);}boolean dfs(TreeNode left, TreeNode right) {if(left==null && right==null) {return true;}if(left==null || right==null) {return false;}if(left.val!=right.val) {return false;}return dfs(left.left,right.right) && dfs(left.right,right.left);}
}
解法二:迭代
首先我们引入一个队列。初始化时我们把根节点入队两次。每次提取两个结点并比较它们的值(队列中每两个连续的结点应该是相等的,而且它们的子树互为镜像),然后将两个结点的左右子结点按相反的顺序插入队列中。当队列为空时,或者我们检测到树不对称(即从队列中取出两个不相等的连续结点)时,该算法结束。
class Solution {public boolean isSymmetric(TreeNode root) {return check(root, root);}public boolean check(TreeNode u, TreeNode v) {Queue<TreeNode> q = new LinkedList<TreeNode>();q.offer(u);q.offer(v);while (!q.isEmpty()) {u = q.poll();v = q.poll();if (u == null && v == null) {continue;}if ((u == null || v == null) || (u.val != v.val)) {return false;}q.offer(u.left);q.offer(v.right);q.offer(u.right);q.offer(v.left);}return true;}
}


![[SwiftUI]系统弹窗和自定义弹窗](http://pic.xiahunao.cn/[SwiftUI]系统弹窗和自定义弹窗)


)




)








