A. We Got Everything Covered!

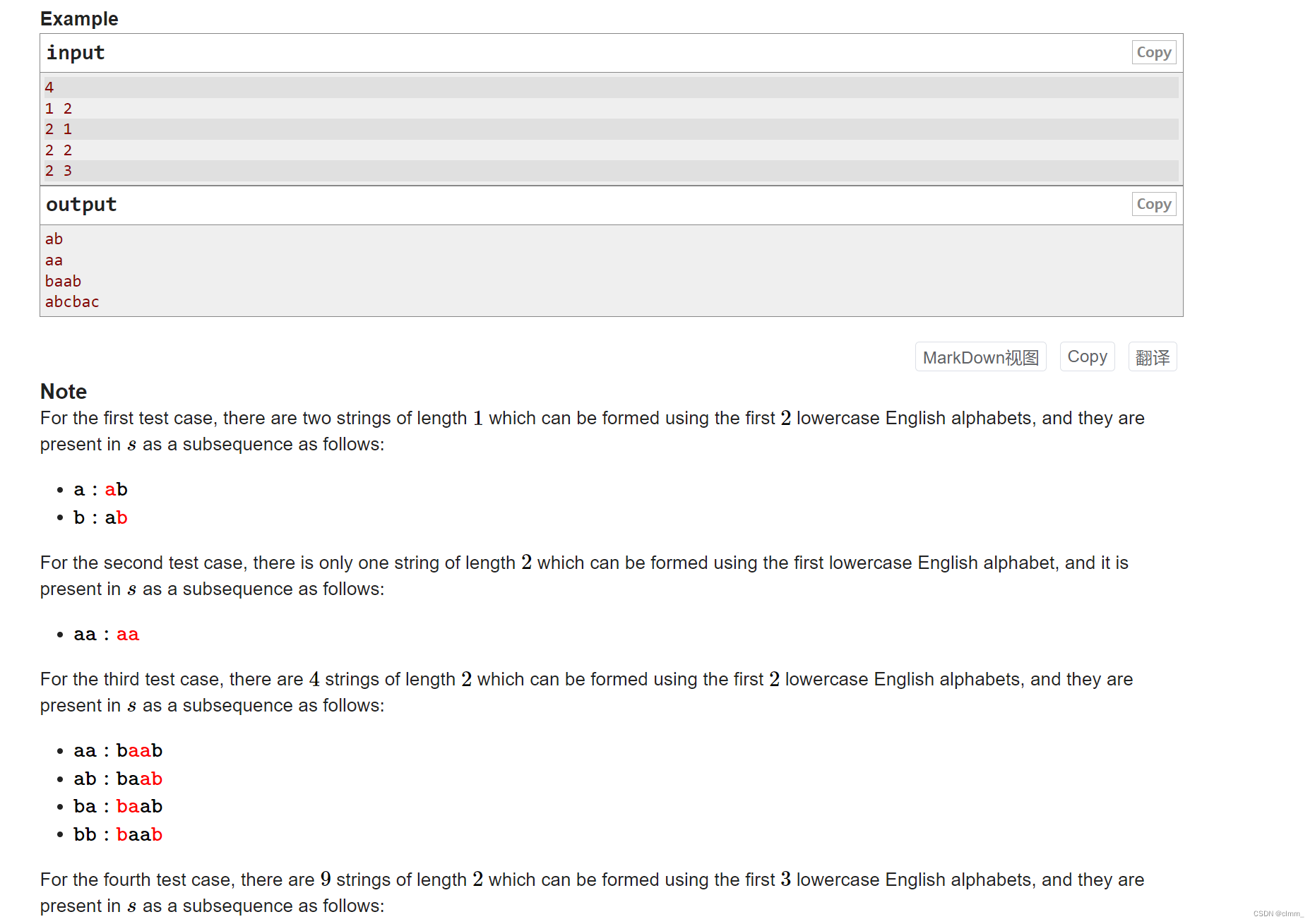
题意：有任意由前k个字母组成的长度为n的字符串s1，你需要构建一个字符串s2，使s1恒为s2的子串（注意是子串，不是连续子串）

分析：我们可以构造n组字符串，每组都包含前k个字母，把这n组字符串拼接起来就是答案。

这题很重要，等会做C题会参考这题的思路

int a[N];
void solve() {int n, k; cin >> n >> k;while (n--) {for (int i = 0; i < k; i++) {printf("%c", 'a' + i);}}cout << endl;
}signed main() {//IOS;int t; t = 1;cin >> t;while (t--) {solve();}return 0;
}

B. A Balanced Problemset?

题意：把x分为n个数，怎么分，能使最小公倍数最大。

分析：首先联想到gcd的性质

GCD(a1, a2, a3, …, an) = GCD(a1, a1 + a2, a1 + a2 + a3, …, a1 + a2 + a3 + … + an)

这意味着n个数的最小公倍数等于这n个数之和的除数。

最小公倍数必定是x的除数。所以我们用试除法求x的除数k，然后判断该除数k可不可以作为这n个数的最小公倍数。

现在我们面临两个问题，怎么分x？分完怎么判断k能不能做为最小公倍数？

我们可以让前n-1个数都为k，然后剩下的数全分给第n个数，如果an%k==0，说明k可以做为最小公倍数。

int d = x - k * (n - 1);
if (d % k == 0 && d > 0) ans = max(ans, k);

试除法时间复杂度:

int a[N];
void solve() {int x, n; cin >> x >> n;//把x分成n组int ans = 1;for (int i = 1; i <= x / i; i++) {if (x % i == 0) {//考虑k1和k2能不能成为最小公倍数int k1 = i, k2 = x / i;//若最小公倍数为k1，k2int d1 = x - k1 * (n - 1);int d2 = x - k2 * (n - 1);if (d1 % k1 == 0 && d1 > 0) ans = max(ans, k1);if (d2 % k2 == 0 && d2 > 0) ans = max(ans, k2);}}//tans;cout << ans << endl;
}signed main() {//IOS;int t; t = 1;cin >> t;while (t--) {solve();}return 0;
}

C. Did We Get Everything Covered?

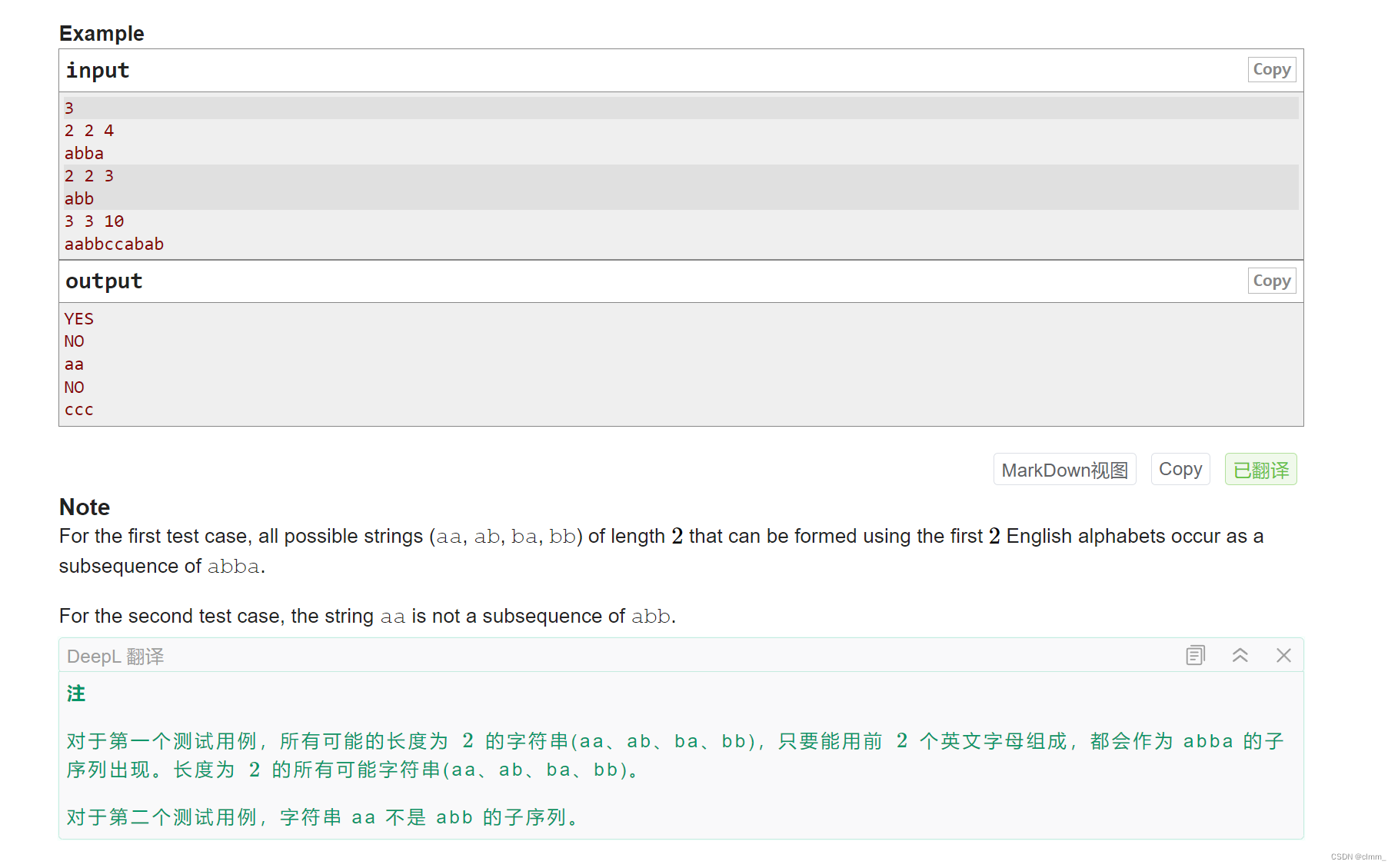
分析：有任意由前k个字母组成的长度为n的字符串集合s1，题目给出了字符串s2，判断s1里所有元素是不是都为s2的子串，如果是输出YES，不是就输出NO并给出反例。

有了刚刚的A题，我们可以知道s2必须满足，“有n组字符串，每组都包含前k个字母”，这个条件时，s1恒为s2子串。那我们就去s2找呗，看能不能满足。

比如说这个，要有3组，每组都必须包含abc这三个字母。

第一组：aabbc

 第二组：cab

第三组：ab，第三组有一个c没包含，我们称第三组是“不满足组”

因此不满足。是NO。反例字符串s3就是cbc（前面每组最后一个字母加上不满足组缺少的字母）。假如此时s3的长度不足n（我们举的反例包含在字符串集合s1里），那就在后面随便加上一些字母凑到长度n就好了。

至于为什么是这样的贪心策略，自己多构造几个样例试一试就有感觉了，真正解释起来好麻烦。