高斯分布，也称为正态分布，是统计学中最常见的概率分布之一。它具有钟形曲线的形态，对称分布在均值周围，且由均值和标准差两个参数完全描述。

高斯分布的概率密度函数（Probability Density Function, PDF）可以用以下公式表示：

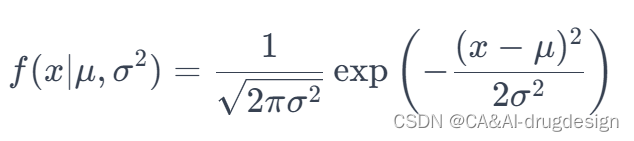
其中：
—x 是随机变量
—μ 是均值（期望值）
—σ2是方差，σ则是标准差

高斯分布的特点包括：

1. 均值（期望值）是分布的中心，决定了曲线的位置。
2. 标准差决定了曲线的宽度，标准差越大，曲线越扁平。
3. 曲线在均值处取得最大值，因此曲线的峰值就是均值。
4. 曲线关于均值对称。

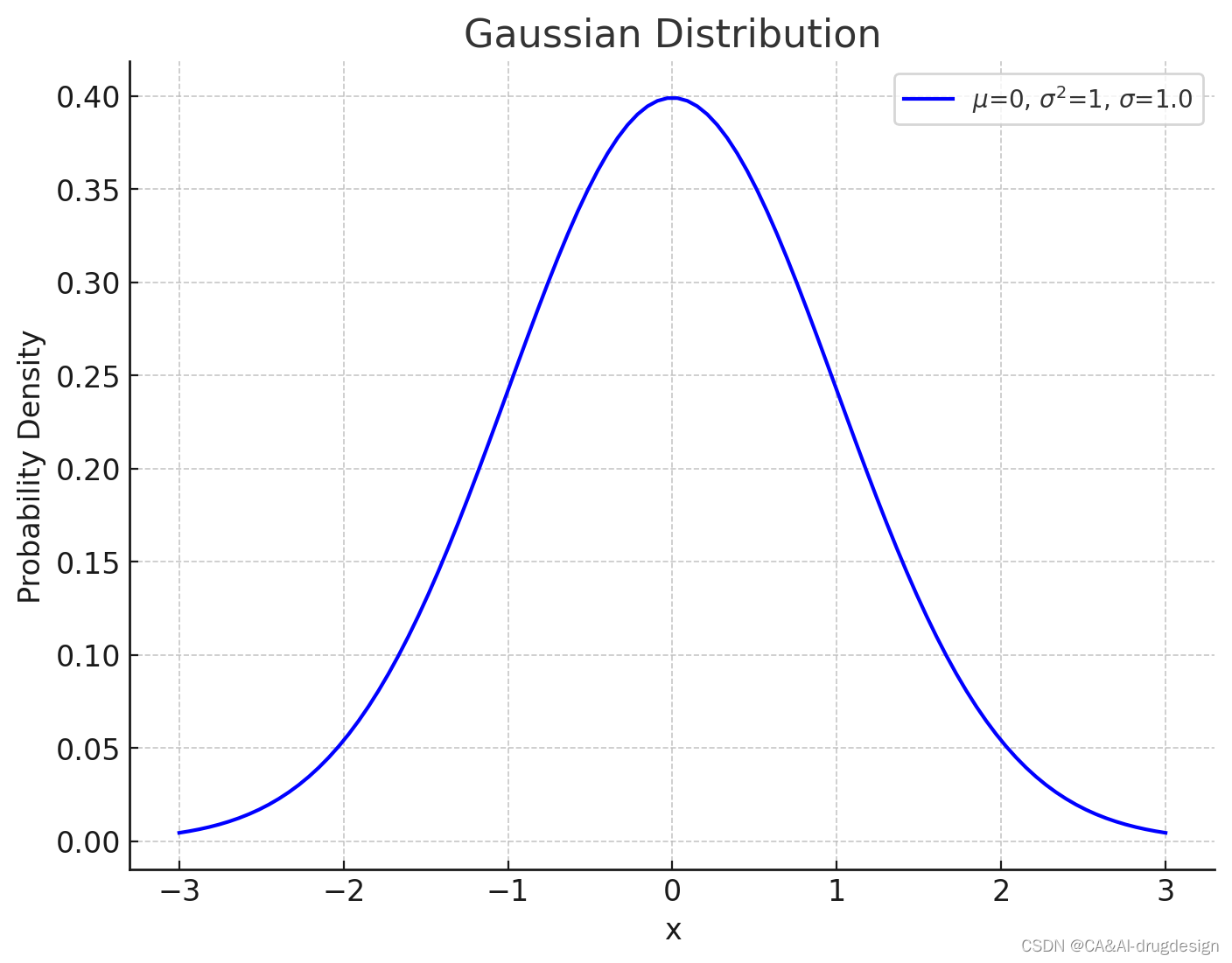
高斯分布在自然界和人类活动中广泛应用，例如，许多测量误差的分布、人口身高、体重、温度变化等都可以近似地用高斯分布描述。在机器学习和统计学中，高斯分布经常用作模型假设，例如，线性回归和贝叶斯推断等领域。