坚持刷题｜平衡二叉树

文章目录

题目
考察点
代码实现
实现总结
对实现进一步改进
扩展提问

坚持刷题，老年痴呆追不上我，今天继续二叉树：平衡二叉树

题目

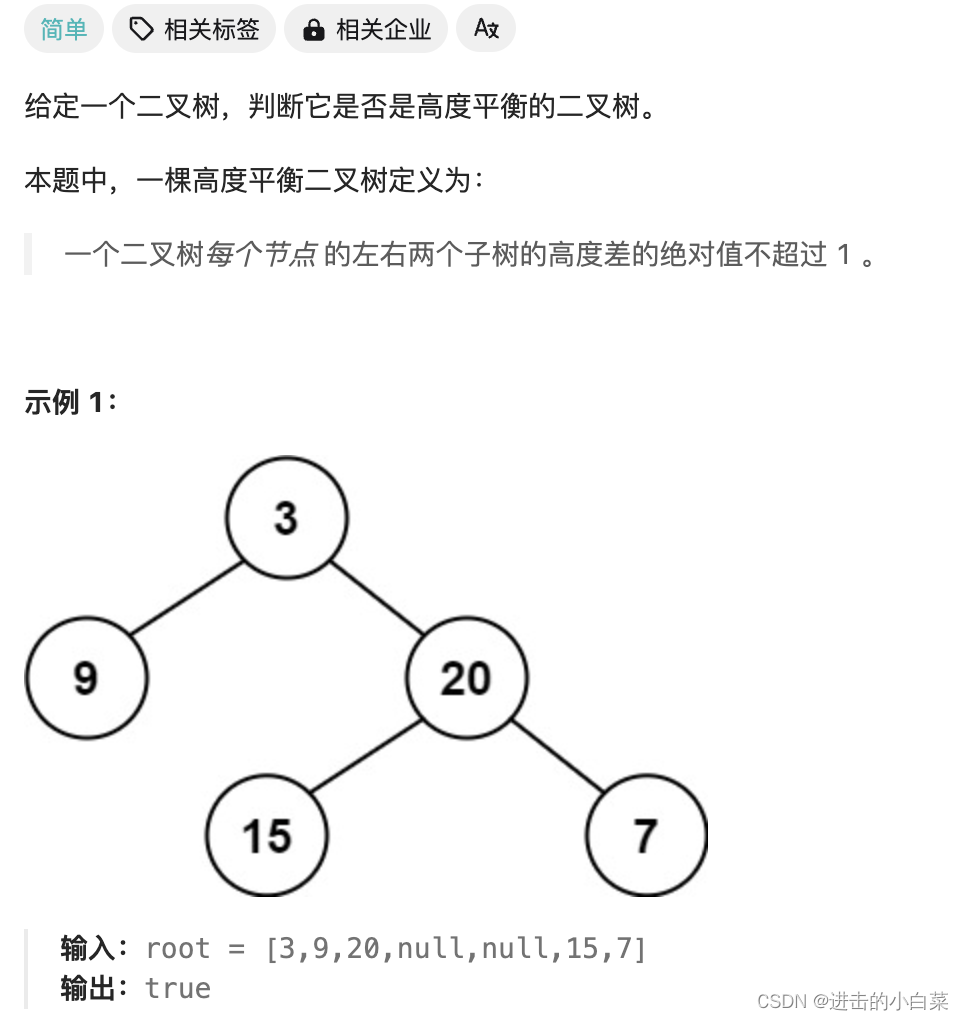
110.平衡二叉树
在这里插入图片描述

考察点

递归能力：能否使用递归来解决问题。
树的基本操作：能否正确地访问节点的值，左子树，右子树等。
理解平衡二叉树：能够理解平衡二叉树的定义。
边界条件处理：能否正确处理空树的情况。
时间和空间复杂度：解决问题的方法是否具有合理的时间和空间复杂度。

代码实现

class TreeNode {int val;TreeNode left;TreeNode right;TreeNode(int x) {val = x;}
}public class BinaryTreeBalance {public boolean isBalanced(TreeNode root) {if (root == null) {return true;}int leftHeight = getHeight(root.left);int rightHeight = getHeight(root.right);// 检查当前节点是否平衡，并递归检查左右子树return Math.abs(leftHeight - rightHeight) <= 1&& isBalanced(root.left)&& isBalanced(root.right);}private int getHeight(TreeNode node) {if (node == null) {return 0;}// 递归计算左右子树的高度，取最大值加上当前节点的高度（1）return 1 + Math.max(getHeight(node.left), getHeight(node.right));}public static void main(String[] args) {BinaryTreeBalance solution = new BinaryTreeBalance();// 在这里构建你的二叉树TreeNode root = new TreeNode(1);root.left = new TreeNode(2);root.right = new TreeNode(3);root.left.left = new TreeNode(4);root.left.right = new TreeNode(5);// 调用isBalanced方法判断是否为平衡二叉树boolean result = solution.isBalanced(root);// 输出结果System.out.println("Is the binary tree balanced? " + result);}
}

实现总结

递归：使用递归来计算每个节点的高度，参考坚持刷题｜二叉树的最大深度，检查左右子树的高度差是否超过1，若超过1，则说明不是平衡二叉树
时间复杂度： O(n log n)。因为对于每个节点，都需要计算其左右子树的高度，而计算高度的时间复杂度是 O(log n)
空间复杂度： O(log n)，递归调用栈的深度等于该节点的高度。在平衡二叉树的情况下，树的高度是 O(log n) 级别的。因此，递归调用的空间复杂度是 O(log n)。需要注意的是，这里的空间复杂度并不仅仅是由递归调用所使用的空间构成，还包括了递归过程中的临时变量、参数传递等所占用的空间。

对实现进一步改进

避免重复计算节点的高度： 在上面的实现中，对每个节点都调用了getHeight方法来计算高度。这可能导致重复计算，尤其是对于同一个节点。为了避免这种情况，可以修改算法，使得在计算高度的同时判断平衡条件。
一边计算高度一边判断平衡条件： 可以在递归调用的过程中，一边计算左右子树的高度，一边判断当前节点是否满足平衡条件。这样可以避免递归两次计算相同节点的高度。

class TreeNode {int val;TreeNode left;TreeNode right;TreeNode(int x) {val = x;}
}public class BalancedBinaryTree {public boolean isBalanced(TreeNode root) {return checkHeightAndBalance(root) != -1;}private int checkHeightAndBalance(TreeNode node) {if (node == null) {return 0;  // 空树是平衡的，高度为0}int leftHeight = checkHeightAndBalance(node.left);if (leftHeight == -1) {return -1;  // 左子树不平衡，直接返回-1}int rightHeight = checkHeightAndBalance(node.right);if (rightHeight == -1) {return -1;  // 右子树不平衡，直接返回-1}// 判断当前节点是否平衡，如果不平衡则返回-1，否则返回当前节点的高度if (Math.abs(leftHeight - rightHeight) > 1) {return -1;} else {return Math.max(leftHeight, rightHeight) + 1;  // 返回当前节点的高度}}public static void main(String[] args) {BalancedBinaryTree solution = new BalancedBinaryTree();// 在这里构建你的二叉树TreeNode root = new TreeNode(1);root.left = new TreeNode(2);root.right = new TreeNode(3);root.left.left = new TreeNode(4);root.left.right = new TreeNode(5);// 调用isBalanced方法判断是否为平衡二叉树boolean result = solution.isBalanced(root);// 输出结果System.out.println("Is the binary tree balanced? " + result);}
}