题目描述
为了从 F F F 个草场中的一个走到另一个,贝茜和她的同伴们不得不路过一些她们讨厌的可怕的树。奶牛们已经厌倦了被迫走某一条路,所以她们想建一些新路,使每一对草场之间都会至少有两条相互分离的路径,这样她们就有多一些选择。
每对草场之间已经有至少一条路径,给出所有 R R R 条双向路的描述,每条路连接了两个不同的草场,请计算最少的新建道路的数量。
路径由若干道路首尾相连而成,两条路径相互分离,是指两条路径没有一条重合的道路,但是两条分离的路径上可以有一些相同的草场。
对于同一对草场之间,可能已经有两条不同的道路,你也可以在它们之间再建一条道路,作为另一条不同的道路。
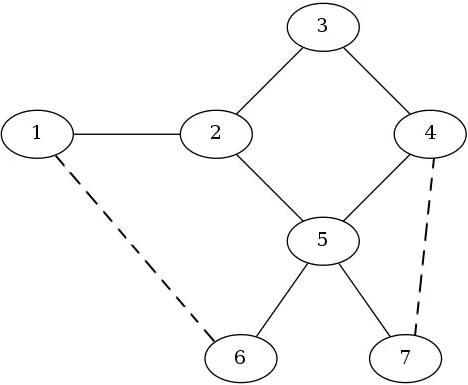
图中实线表示已有的道路,
输入输出格式
输入格式:
第一行输入两个整数 F F F 和 R R R;
接下来 R R R 行,每行输入两个整数,表示两个草场,它们之间有一条道路。
输出格式:
输出最少需要新建的道路数目。
输入输出样例
输入样例#1:
7 7
1 2
2 3
3 4
2 5
4 5
5 6
5 7
输出样例#1:
2
解法
tarjan缩点,然后求出有多少只有一条边的节点,答案就是 节点个数÷2
#include <bits/stdc++.h>
using namespace std;
const int N=3e5;
struct edge {int v,net;
} e[N];
int n,m,x,y,tp,sc,ans,cnt,idx,a[N],pst[N],fa[N],head[N],scc[N],low[N],dfn[N],sta[N];
void add(int u,int v) {e[++cnt].v=v;e[cnt].net=head[u];head[u]=cnt;
}
void tarjan(int u,int f) {low[u]=dfn[u]=++idx;sta[++tp]=u;fa[u]=f;for (int i=head[u]; i; i=e[i].net) {int v=e[i].v;if (v==f) continue;if (!dfn[v]) {tarjan(v,u);low[u]=min(low[v],low[u]);} elselow[u]=min(low[u],dfn[v]);}if (dfn[u]==low[u]) {sc++;while (sta[tp+1]!=u) {scc[sta[tp]]=sc;tp--;}}
}
int main() {scanf("%d%d",&n,&m);for (int i=1; i<=m; i++) {scanf("%d%d",&x,&y);add(x,y);add(y,x);}for (int i=1; i<=n; i++)if (!dfn[i])tarjan(i,i);for (int i=1; i<=n; i++) {if (scc[i]!=scc[fa[i]]) {a[scc[i]]++;a[scc[fa[i]]]++;}}for (int i=1; i<=sc; i++) {if (a[i]==1)ans++;}printf ("%d",(ans+1)/2);return 0;
}
)




服务器电脑IEC 60320电源线)






![[计算机提升] 清理系统盘的前期准备](http://pic.xiahunao.cn/[计算机提升] 清理系统盘的前期准备)






