一.排序
1.什么是稳定性
2.分类
二.插入排序
1.直接插入排序
原理:当插入第i个数时,前面i-1个数据已经排好序了。只要用第i个数据和第i-1,i-2,i-3个数据依次进行比较,找到合适的位置插入,后面的数据一次后移即可
例如1,3,2,24,35,11 从大到小排,从第二个数开始定义一个临时变量tmp存放要排的数据3,此时1下标就是空的,定义一个i表示要进行比较的数的下标,此时i=0,3和1比,3大,所以把1放到1下标,i向前走发现i<0了,所以i就不向前走了,把tmp的值就放到i下标;假设11以前都排好了,即35,24,3,2,1,11,现在排11,tmp=11,初始i=4,tmp与4下标的数比较,11比1大,所以1放到5下标,i再向前走,11比2大,所以2放到4下标(即i-1下标),i再向前走,11比3大,所以3放到3下标(即i-1下标),i再向前走,24比11小,所以把11也就是tmp的值放到2下标(即i-1下标)。
代码如下

总结
1.时间复杂度:O(N^2);因为比较次数是依次递增,即1+2+3+4+……+(n-1).
2.空间复杂度:O(1);因为该代码使用的变量是常数个。
3.稳定性:稳定的
4.元素集合越接近有序,需要比较的次数就越少,时间效率就越高。比如从小到大排序1,2,3,4,5,已经有序了,只需遍历到每个元素即可,不需要回退,此时时间复杂度为O(N)。
5.适用于待排序序列已经基本接近有序
2.希尔排序(直接插入排序的优化)
希尔排序法又称为缩小增量排序法,把一组数分为若干组,每组进行直接插入排序
例如下图:
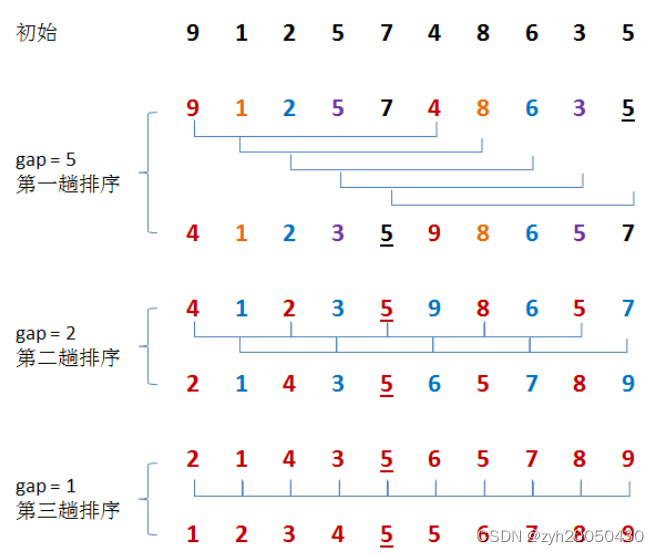
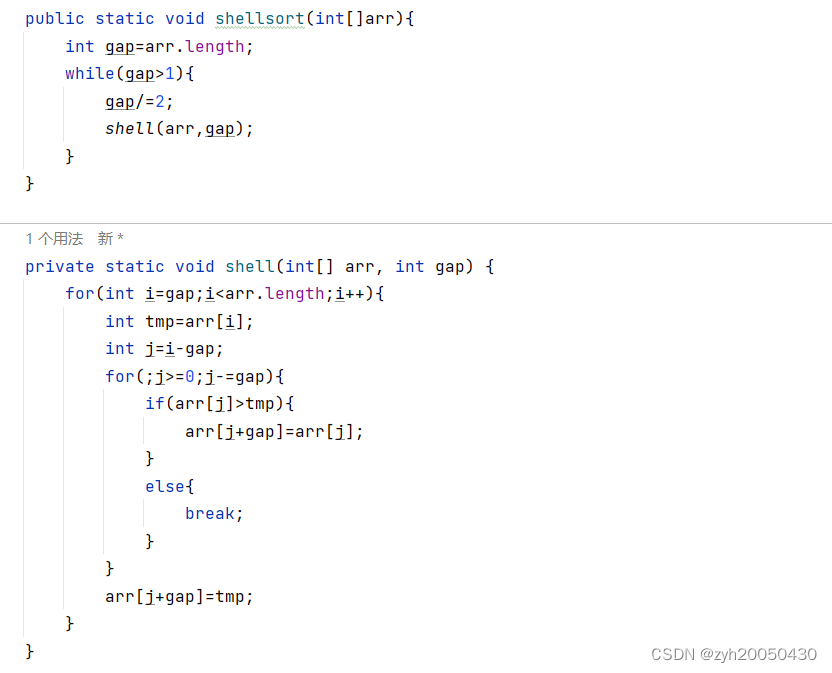
总结
1.时间复杂度:尚未有明确的规定,可以是n^1.3~n^1.6,也可以是n^1.25~1.6*n^1.25。
2.空间复杂度:O(1)。因为一直是在原数组上进行操作,没有额外开辟空间
3.稳定性:不稳定,原因是存在不相邻记录的交换。比如1,5,3,3,4,6,分成俩组进行从小到大排序,第一组是1,3,4,不用交换,第二组是5,3,6,需要交换变成3,5,6,这就导致第二个3跑到了第一个3的前面
三.选择排序
1.直接选择排序
定义一个i,从0下标开始遍历数组;再定义一个minindex,初始值为i,从i+1下标开始到n-1,每次将该下标的值与minindex下标的值进行比较,如果小于minindex下标的值,就将minindex更新为当前下标,最后将minindex与i下标的值进行交换,i++,到最后,该数组就是从小到大排序。代码如下:
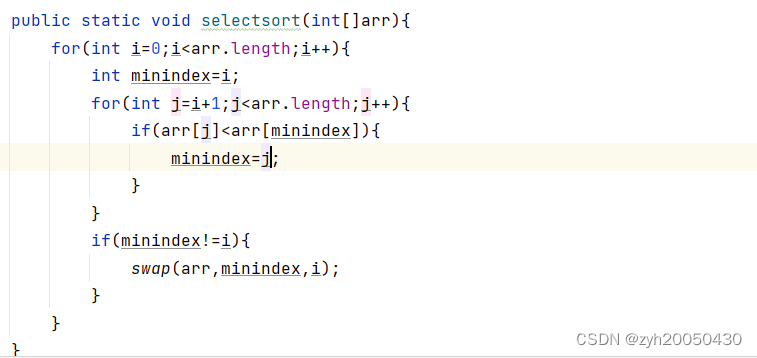
总结
1.时间复杂度:O(N^2)
2.空间复杂度:O(1)
3.稳定性:不稳定,比如5,8,5,1,7要从小到大排序,我们知道,第一趟结束,5会和1进行交换,这是第一个5就到了第二个5之后,所以不稳定。
4.缺点:对于已经有序的数组,它还是会无脑的遍历从i到n-1的每一个数据,导致无论是最好情况下还是最坏情况下,都是O(N^2)。
2.双向选择排序
定义maxindex和minindex,定义left=0,right=arr.length-1,初始maxindex和minindex都等于left,然后遍历left到right下标的值,更新maxindex和minindex,最后将left下标与minindex下标的值进行交换,将right下标与maxindex下标的值进行交换,然后left++,right--。
代码如下:
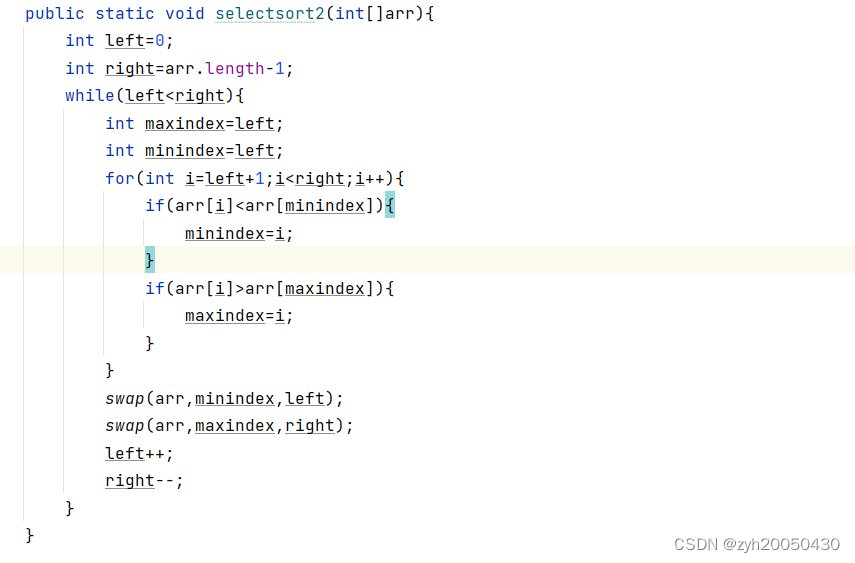
但注意,这段代码有问题,如果maxindex就是left,那么mindex与left交换之后,maxindex指向的就是最小值了,直接让maxindex与right交换就会出问题,所以进行如下改进:

总结
1.时间复杂度:O(N^2)
2.空间复杂度:O(1)
3.稳定性:不稳定
3.堆排序
排升序建立大堆,排降序建立小堆。以升序为例:定义一个end,初始指向arr.length-1,将大根堆的0下标元素与end指向的元素交换,此时end下标的元素就是有序的,再将0下标元素进行向下调整(范围是0~end);然后end--,再与0下标的值进行交换,再向下调整……
代码如下:
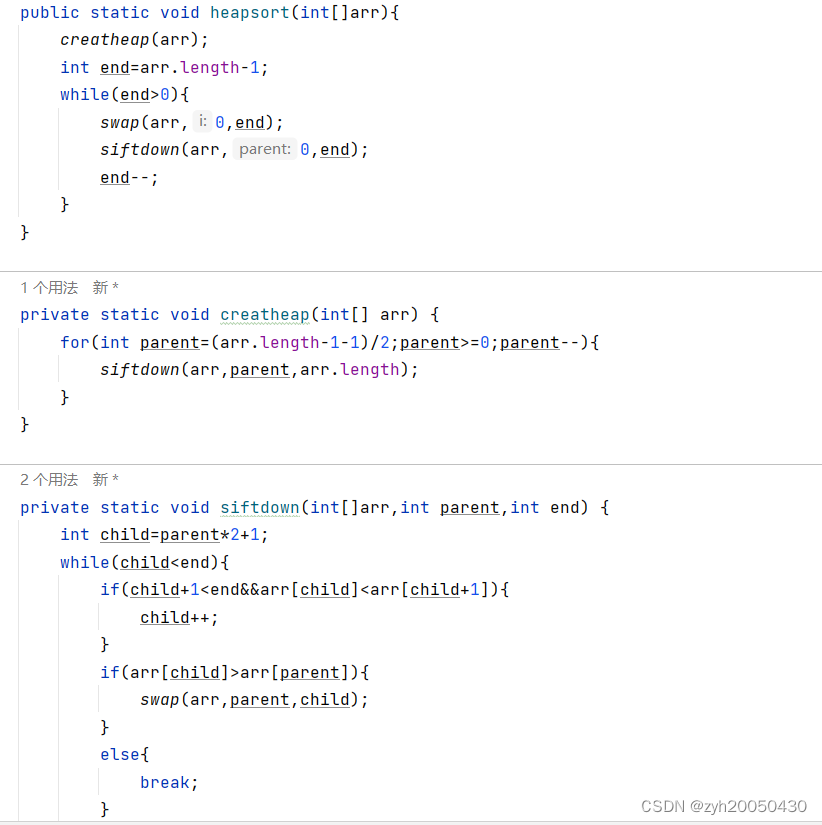
总结
1.时间复杂度:O(N*log2N)。因为向下建堆的时间复杂度为O(N),而从0到end进行向下调整的全过程的时间复杂度为O(N*log2N),所以O(N)可以忽略不记,只记O(N*log2N)
2.空间复杂度:O(1)。
3.稳定性:不稳定。
四.交换排序
1.冒泡排序
代码如下:

优化:
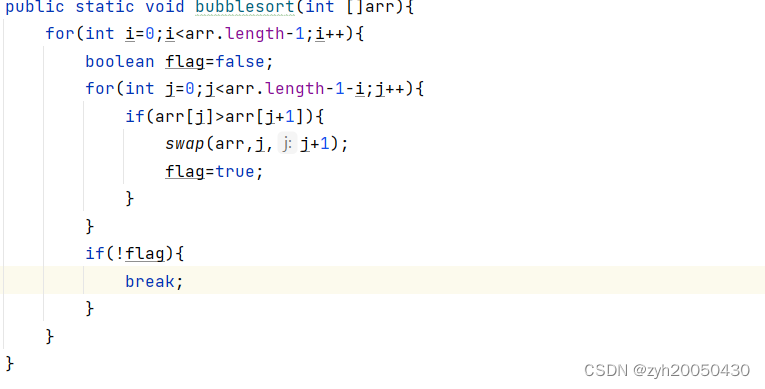
总结
1.时间复杂度:O(N^2)。
2.空间复杂度:O(1)。
3.稳定性:稳定。
2.快速排序
(1).Hoare版
以0下标的数为基准值,初始化left=1,right=arr.length-1,right先向左移动,找到比0下标小的数就停止,然后left向右移动,找到比0下标的值大的数就停止,之后left和right下标的值进行交换,然后再让right移动,left移动,重复上述过程,直到left和right相遇时,设相遇时的下标为flag,就将0下标的值与flag下标的值进行交换;然后进行递归,就是让flag的左边和右边都进行Hoare版的快速排序。代码如下:
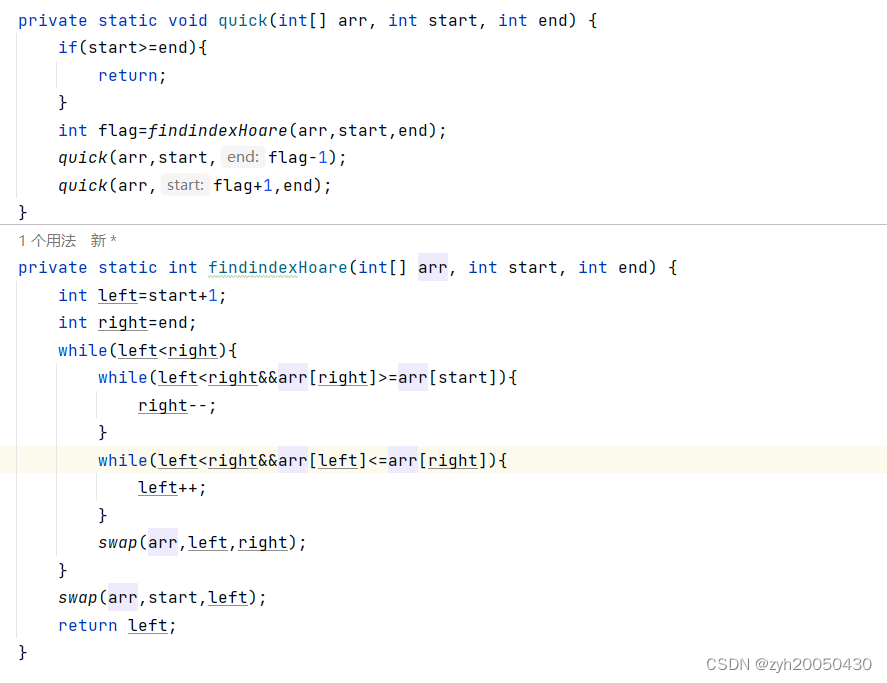
注意:必须先让right找小的,因为最终是left与right相遇的地方即flag和0下标交换,此时原来0下标的值就在原来flag下标的值的右边,如果先让left找大数,就可能会导致把比基准值大的数放到了基准值的左边,而先让right找就没问题
(2).挖坑法
先将第一个数据存放在临时变量key中,形成一个坑位,然后right向左走,找到比key小的数,拿起来放到0下标处,此时的坑位转移到了right下标,然后让left向右走,找到比key大的数,将它拿起来放到right下标,此时坑位转移到了left处,依此类推,直到left与right相遇后将key的值放到相遇处,并以相遇处为分割线进行左右递归,代码如下:
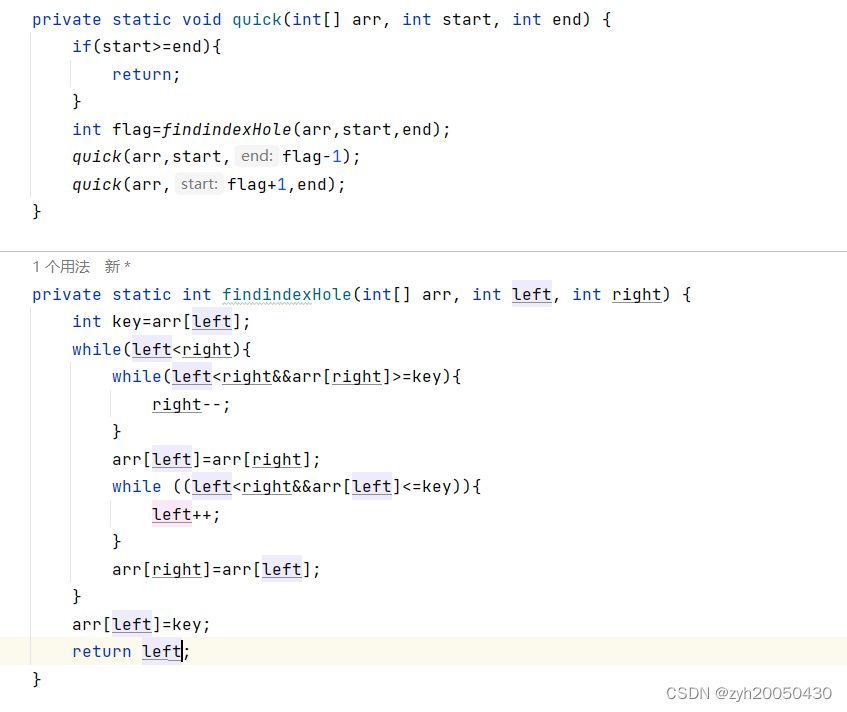
注意,必须是arr[right]>=key,等号不可以忽略,否则就会死循环。比如6,1,3,4,7,6,left=0,right=5,6大于6吗?不大于,所以第一个while进不去,所以将right的值给到left下标,即6和6进行交换,然后进行第二个while的判断,又进不去,所以又交换……一直这样死循环。
(3).前后指针法
定义key指向0下标,初始化prev指向0,初始化cur指向0,cur往后走找到一共比key指向的数据小的值时停止,然后prev先++,如果prev和cur指向的不是同一个数,就让prev指向的数与cur指向的数交换,然后cur再去找下一个比key小的数,直到cur走到头后,让key下标的值与prev下标的值进行交换,返回prev,再以prev为基准,左右向这样去递归。代码如下:
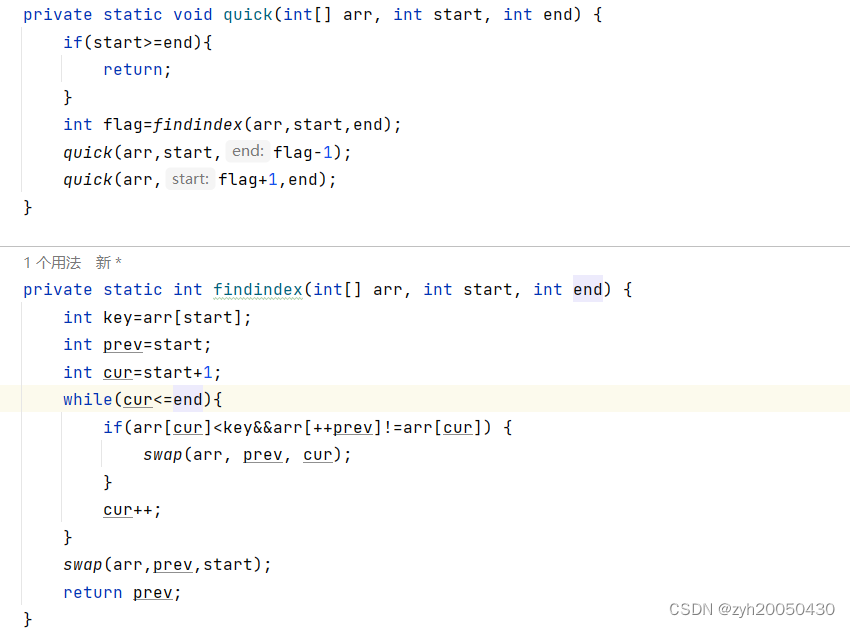
总结
1.时间复杂度:O(N*log2N)。这可以说是最好情况下是O(N*log2N),即每一次找到的flag都是在这组数据的中央,第一层是一整组,共n个数据,都要遍历到;第二层是从中央的flag分开成俩组,每组n/2个数据,都要遍历到……一共有log2n层,每层都是遍历到n个数据,所以是O(N*log2N)
而最坏情况下是O(N^2),即每次找到的flag都是第一个数据,导致没有左边,只有右边,所以这种情况下是:第一层遍历n个数据进行比较,第二层是n-1个数据,第三层是n-2个数据……一共是n层。
2.空间复杂度:O(log2N)。这主要与函数的递归调用有关。实际上,O(log2N)是最好情况下,也就是每次找到的基准值的下标都是中间值,所以先对基准值的左边进行递推,一共log2n层,所以在栈上开辟了log2n个空间,然后回退,直到把左边递归完,再此同时把这log2n个空间回收,然后对右边进行递归,又是开辟log2n个空间……总的来说就是O(log2N)
最坏情况下就是基准值一直是第一个,导致一共要开辟n个空间,所以是O(N)。
3.稳定性:不稳定,比如6,7,3,4,5,10,3,第一次就是7和最后一个3进行交换,导致俩个3的位置发生了改变
4.缺点:当数组数据过多,递归次数过大时,可能会造成栈溢出
3.快速排序的优化
出发点:减少递归的次数,也就是尽量让数组变成一棵完全二叉树,让基准值尽量为中间值
(1).三数取中法选基准
定义left,right,再定义mid=(left+right)/2,选取三个下标对应的数中的中位数,将其与left下标的数进行交换,然后再用上面的三个方法返回flag下标,再去递归,这样可以减少基准值总是在头或尾的情况。代码如下:
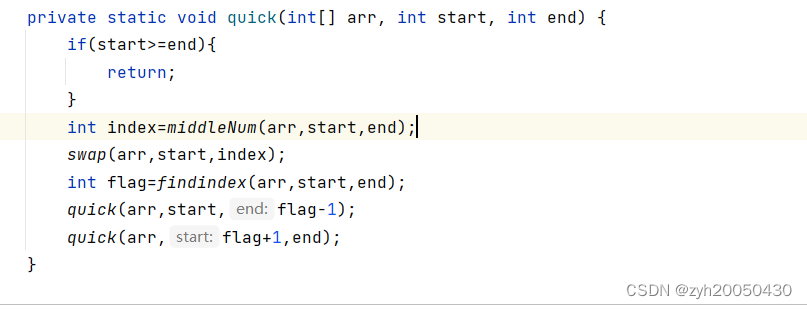

(2).递归到小的子区间时,可以用直接插入排序
就是说,越往下递归,数据越有序,选择直接插入排序的时间效率就会越高,所以可以在三数取中法的基础上再如下优化:
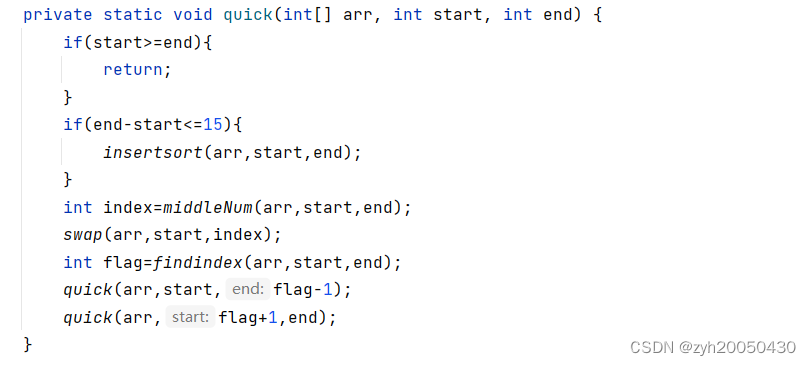
(3).非递归的快速排序
用到了栈。首先定义start和end,先找到基准值的下标,然后将基准值左半部分的开头和结尾的下标存到栈中,再将基准值右半部分的开头和结尾的下标存到栈中,注意,如果基准值左侧不够俩个元素,就不能将左侧的开头和结尾的下标存到栈中,右边也同理(如果flag-1>start,就说明左边够俩个元素,如果flag+1小于end,就说明右边够俩个元素)。然后弹出一个数给到end,再弹出一共数给到start,再去找基准值,以此进行循环,而不是递归,直到栈为空。
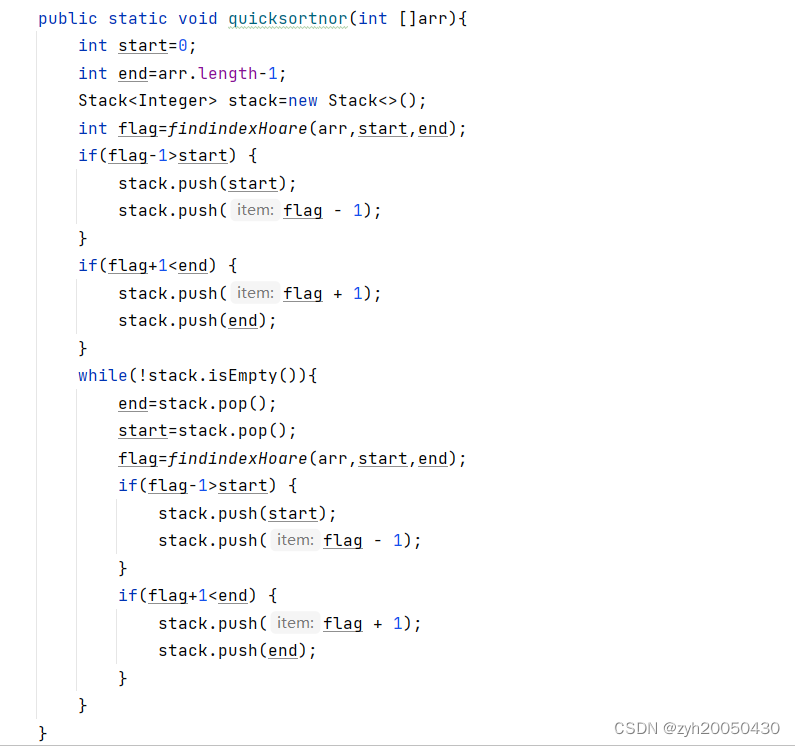
五.归并排序
1.递归实现归并排序
对于一个数组1,6,5,2,3,7,4,9,先将它分裂,分成左右俩半,再将左边分成左右俩半,再将右边分成左右俩半,直到每组只有一个数据,然后让每组先在内部进行排序,然后左右俩组再进行排序(此时就是俩个有序数组的排序,叫做二路归并)。
代码如下:
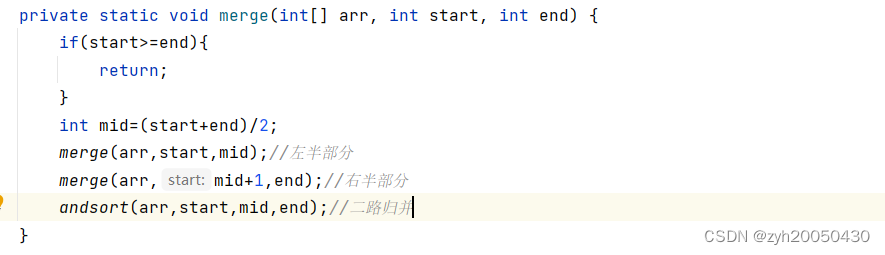
起初start=0,end=arr.length-1,然后进行分裂,最后回归后进行二路归并。二路归并代码如下:
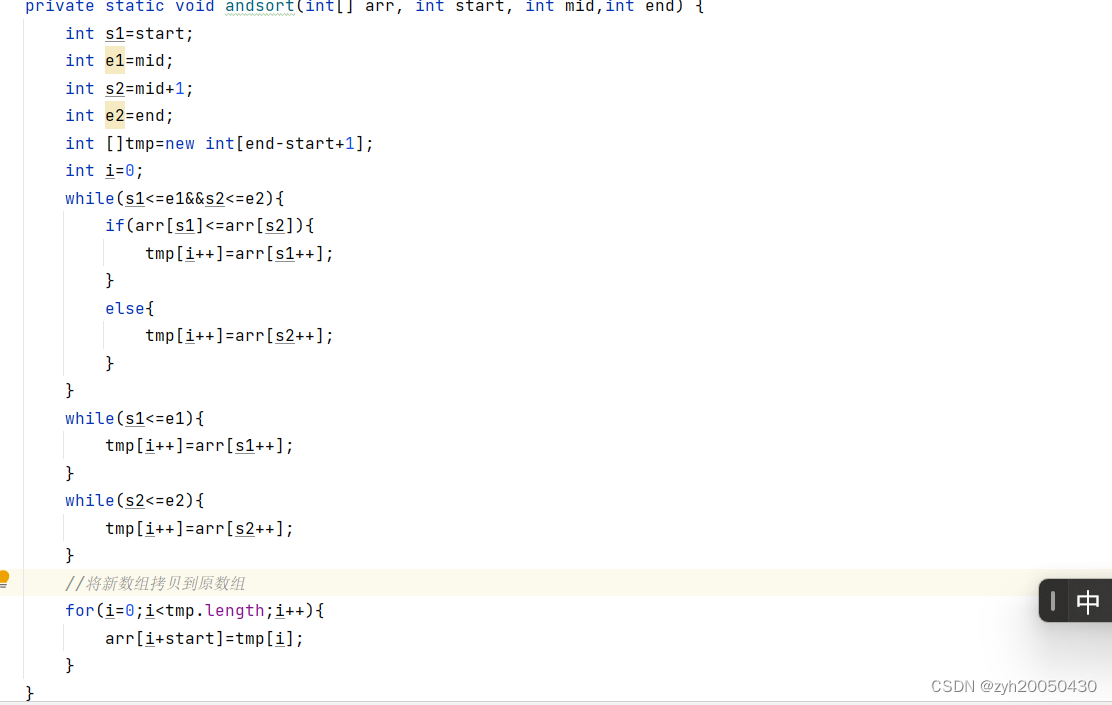
对于已经有序的俩个数组,比如:1,4,6,7和2,3,5,9,定义s1,e1,s2,e2,比较s1,s2对应的数,如果s1小,就将s1对应的数拷贝到tmp数组,然后s1++,反之s2++。直到s1>e1或s2>e2时结束,此时如果s1<=e1,说明左面的数还没有完全拷贝到tmp中,因为已经有序,所以直接拷贝即可,反之操作s2
总结
1.时间复杂度:O(Nlog2N)。这个数组最终被拆成了一棵完全二叉树,所以一共经历了log2N层,在回退进行二路归并时,每层都遍历了n个元素,所以是O(log2N)。
2.空间复杂度:O(log2N)。一共log2N层,就是开辟了log2N个空间后才开始回收空间去递归另一边。
3.稳定性:稳定
2.非递归实现归并排序
先一个一个有序,然后俩个俩个有序,然后四个四个有序……
代码如下:
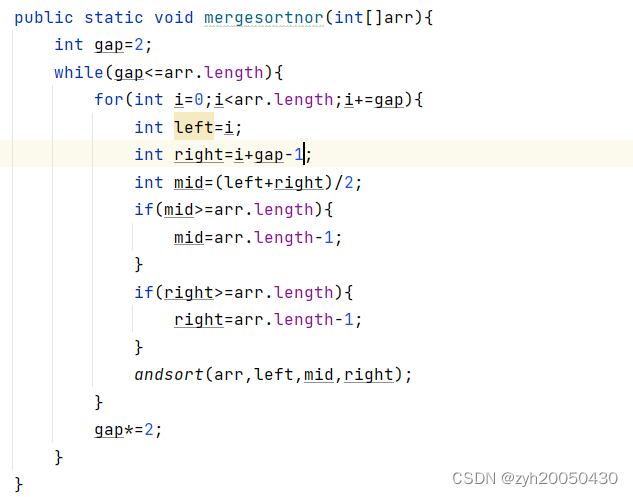
比如数组1,4,2,3,6,5,3,2,首先每组一个数据,已经有序,所以从每组两个数据开始,14,23,65,32,left=i,right=i+gap-1,二路归并后得到14,23,56,23,然后变成每组四个数,即1423,5623,进行二路归并排序(第一路是left到mid,第二路是mid+1到right),得到1234,2356,最后gap=8,再排序。但这样的代码有错误,对于数组长度不是2^n的就不适用,比如1,4,2,6,5,3,共6个数,gap=2时变成14,26,35,然后当gap=4时,i初始为0,i+=gap得到4,那么第二组的left=4,right=7超了,所以right变成5,同理mid也是5,排完变成1246,35,最后按理说应该再对整体排序,但gap=8超过数组长度了,所以最后一组排序没有正常进行,所以这个代码不适用
代码修改:真正实现显性的两个有序数组的合并,即每次i+=gap*2,直接俩组俩组的操作
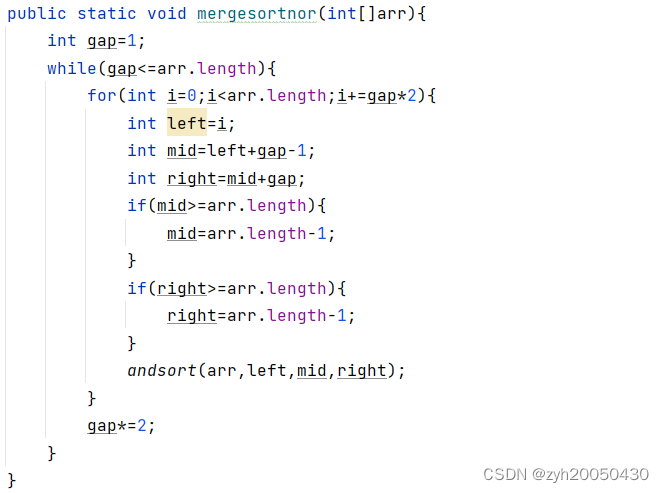
对于数组3,1,2,5,7,1,首先gap=1,分成每组一个,已经有序,然后俩组俩组进行二路归并排序,首先是第1,2组,left=0,mid=0,right=1,……得到13,25,17,然后gap=2,即每组俩个数,两组进行归并排序,前俩组得到1235,后面i=4时,left=4,mid=5,right=8,right超了,所以变成right=5,再去归并排序,此时的俩个有序数组是17和空数组;最后gap=4,i=0时,left=0,mid=3,right=7超了,所以right=5,此时的俩个有序数组是1235和17,再去二路归并排序。这样就能全部排好序了
我们不难发现,改进后的代码中left和mid恰好是第一个有序数组的首尾,mid+1和right正好是第二个有序数组的首尾,而且第二个有序数组的长度可以小于gap甚至为0。而之前的代码可能排序不完善





)
-Redis的性能瓶颈分析)








)



