我们之前说着色过程中以及这个计算法线的时候需要用到这个插值（Interpolation），然后插值是通过这个重心坐标（Barycentric Coordinates）来实现的

目录

重心坐标

插值

---

重心坐标

注意哈我们这里说的三角形的重心坐标并不是指这个三角形重心的坐标，而是指一套坐标系，这套坐标系（α，β，γ）用来表示三角形这个平面上的点，三角形有这个三个顶点的坐标A、B、C，那么这个平面上的点可以表示为（x，y）=αA+βB+γC，其中α+β+γ=1，那么这个（α，β，γ）就是这个点的重心坐标，当α，β，γ都非负时，这个点在三角形内

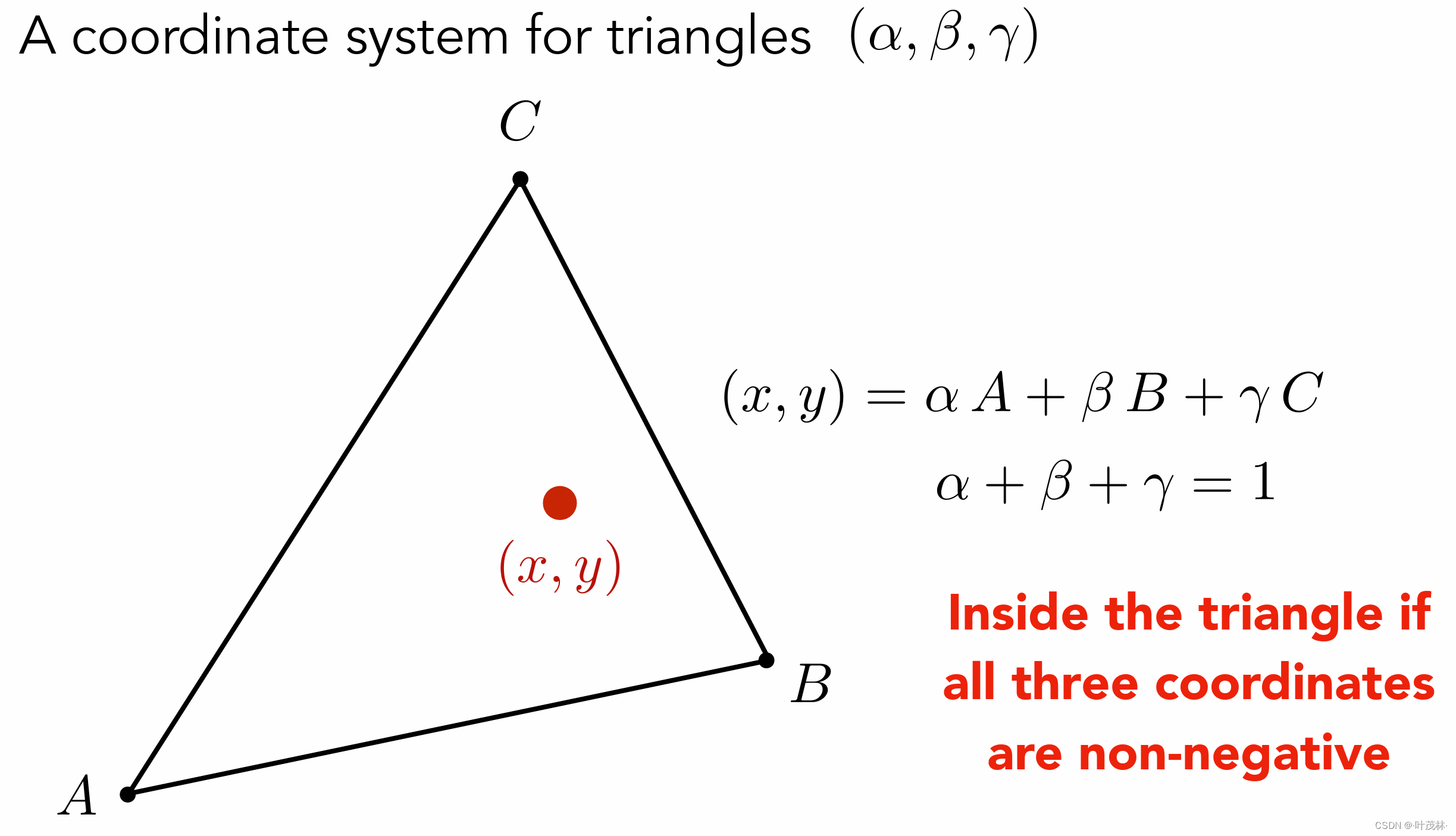
自然三角形的三个顶点的重心坐标就是A（1，0，0）、B（0，1，0）、C（0，0，1）了 

那如何计算任意一个点的重心坐标呢，这个是可以通过面积比来计算的，对于三角形内的任意一个点，它可以和三个顶点连线形成三个小三角形，那么这个点的重心坐标就是对应小三角形和大三角形的面积比

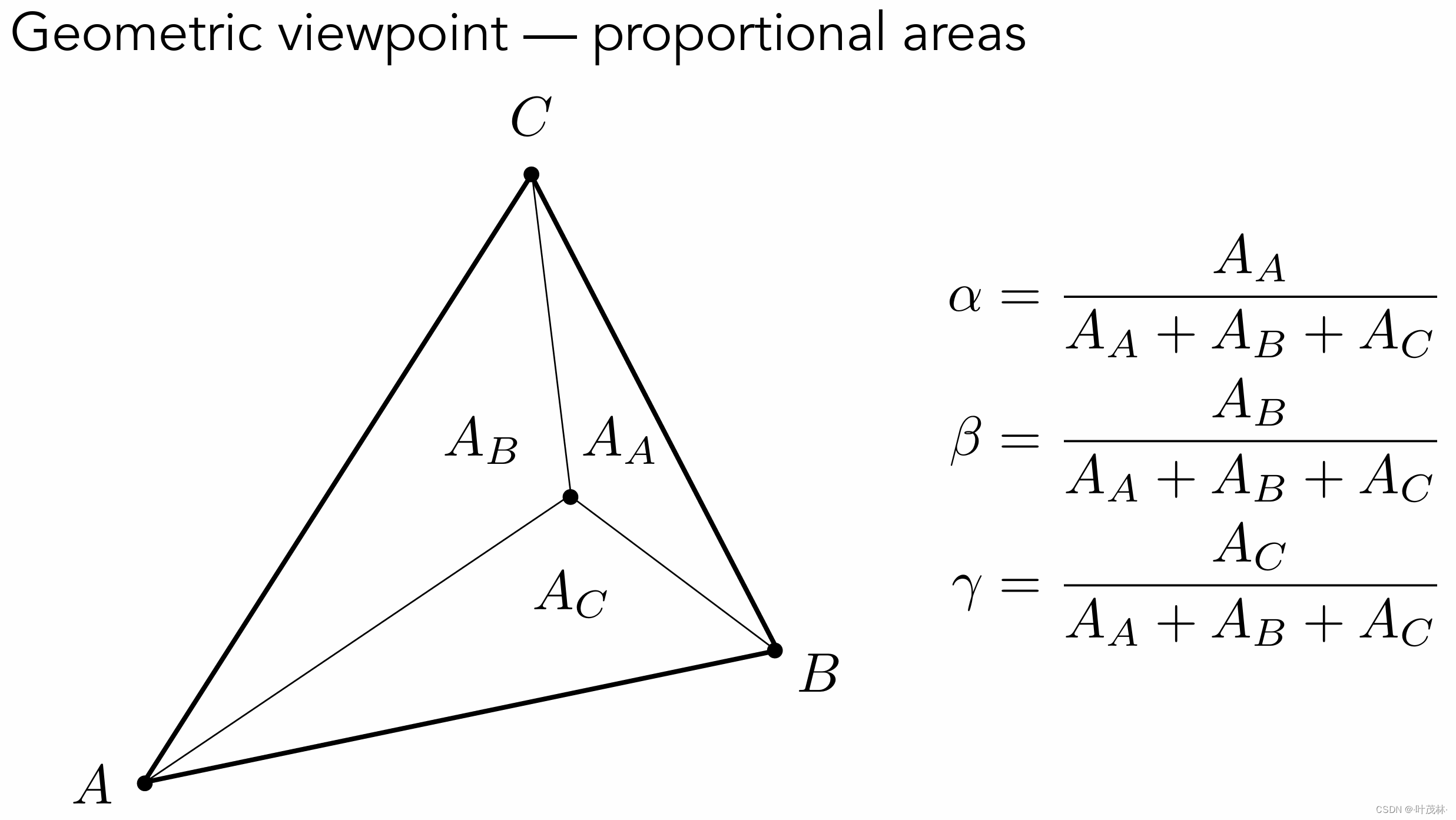
由此我们可以知道三角形重心的重心坐标是什么，因为重心和三个顶点连线所形成的三个三角形面积相等嘛，然后重心的重心坐标就是（⅓，⅓，⅓）

 实际上由刚刚的面积比计算方法可以推出一种《简化》的计算方法

插值

有了重心坐标后，对于已知三角形三个顶点的属性（比方说位置、纹理、坐标、颜色、法线、深度、材质等等），都可以通过插值来计算出三角形内部任意点的属性，并且是看起来平滑过渡的，那怎么做呢？我们不是已经有重心坐标（α，β，γ）了吗，那么对于任意点的属性都可以通过三个顶点的属性进行（α，β，γ）的线性组合得到

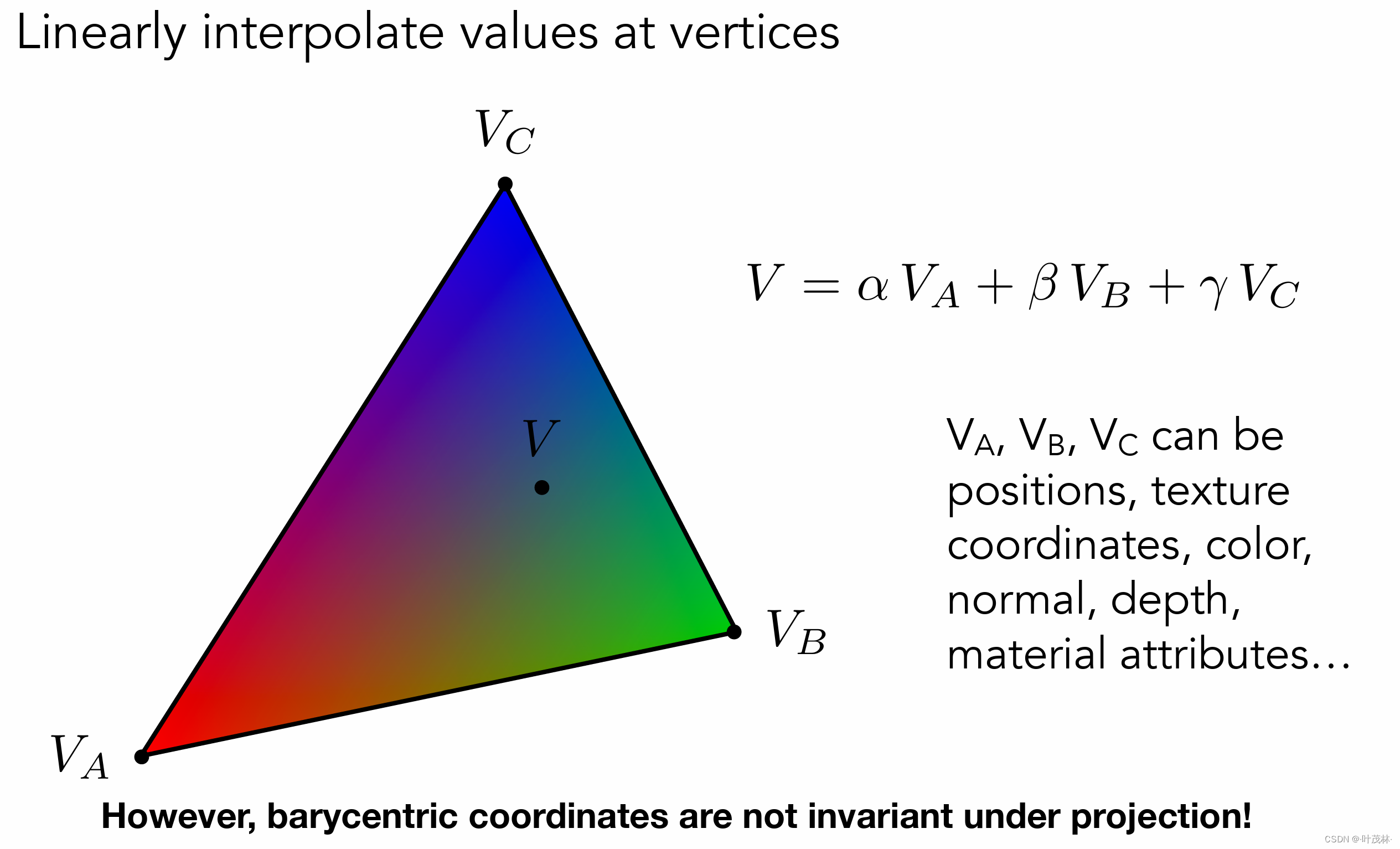
这里需要注意的是，在投影变换的时候，应该先做这个插值再投影