代码随想录算法训练营第14天 | 二叉树的前序、中序、后序遍历（递归+迭代法）

二叉树的理论基础：（二叉树的种类，存储方式，遍历方式以及二叉树的定义）
https://programmercarl.com/%E4%BA%8C%E5%8F%89%E6%A0%91%E7%90%86%E8%AE%BA%E5%9F%BA%E7%A1%80.html

二叉树的递归遍历

Leetcode对应的三道习题：
144.二叉树的前序遍历
145.二叉树的后序遍历
94.二叉树的中序遍历
这个的话，还是比较容易的。就是依次按照他的访问顺序进行递归遍历即可。

// 前序遍历·递归·LC144_二叉树的前序遍历
class Solution {public List<Integer> preorderTraversal(TreeNode root) {List<Integer> result = new ArrayList<Integer>();preorder(root, result);return result;}public void preorder(TreeNode root, List<Integer> result) {if (root == null) {return;}result.add(root.val);preorder(root.left, result);preorder(root.right, result);}
}
// 中序遍历·递归·LC94_二叉树的中序遍历
class Solution {public List<Integer> inorderTraversal(TreeNode root) {List<Integer> res = new ArrayList<>();inorder(root, res);return res;}void inorder(TreeNode root, List<Integer> list) {if (root == null) {return;}inorder(root.left, list);list.add(root.val);             // 注意这一句inorder(root.right, list);}
}
// 后序遍历·递归·LC145_二叉树的后序遍历
class Solution {public List<Integer> postorderTraversal(TreeNode root) {List<Integer> res = new ArrayList<>();postorder(root, res);return res;}void postorder(TreeNode root, List<Integer> list) {if (root == null) {return;}postorder(root.left, list);postorder(root.right, list);list.add(root.val);             // 注意这一句}
}

二叉树的迭代遍历（非递归）

递归的实现就是：每一次递归调用都会把函数的局部变量、参数值和返回地址等压入调用栈中，然后递归返回的时候，从栈顶弹出上一次递归的各项参数，所以这就是递归为什么可以返回上一层位置的原因。

1.前序遍历（迭代法）

前序遍历是中左右，每次先处理的是中间节点，那么先将根节点放入栈中，然后将右孩子加入栈，再加入左孩子。因为这样出栈的时候才是中左右的顺序。

// 前序遍历顺序：中-左-右，入栈顺序：中-右-左
class Solution {public List<Integer> preorderTraversal(TreeNode root) {List<Integer> result = new ArrayList<>();if (root == null){return result;}Stack<TreeNode> stack = new Stack<>();stack.push(root);while (!stack.isEmpty()){TreeNode node = stack.pop();result.add(node.val);if (node.right != null){stack.push(node.right);}if (node.left != null){stack.push(node.left);}}return result;}
}

2.后序遍历（迭代法）

先序遍历是中左右，后续遍历是左右中，那么我们只需要调整一下先序遍历的代码顺序，就变成中右左的遍历顺序，然后在反转result数组，输出的结果顺序就是左右中了，如下图：
在这里插入图片描述

// 后序遍历顺序 左-右-中 入栈顺序：中-左-右 出栈顺序：中-右-左， 最后翻转结果
class Solution {public List<Integer> postorderTraversal(TreeNode root) {List<Integer> result = new ArrayList<>();if (root == null){return result;}Stack<TreeNode> stack = new Stack<>();stack.push(root);while (!stack.isEmpty()){TreeNode node = stack.pop();result.add(node.val);if (node.left != null){stack.push(node.left);}if (node.right != null){stack.push(node.right);}}Collections.reverse(result);return result;}
}

3.中序遍历（迭代法）

刚刚写的前序遍历的代码，不能和中序遍历通用，因为前序遍历的顺序是中左右，先访问的元素是中间节点，要处理的元素也是中间节点，所以刚刚才能写出相对简洁的代码，因为要访问的元素和要处理的元素顺序是一致的，都是中间节点。

那么再看看中序遍历，中序遍历是左中右，先访问的是二叉树顶部的节点，然后一层一层向下访问，直到到达树左面的最底部，再开始处理节点（也就是在把节点的数值放进result数组中），这就造成了处理顺序和访问顺序是不一致的。

那么在使用迭代法写中序遍历，就需要借用指针的遍历来帮助访问节点，栈则用来处理节点上的元素。
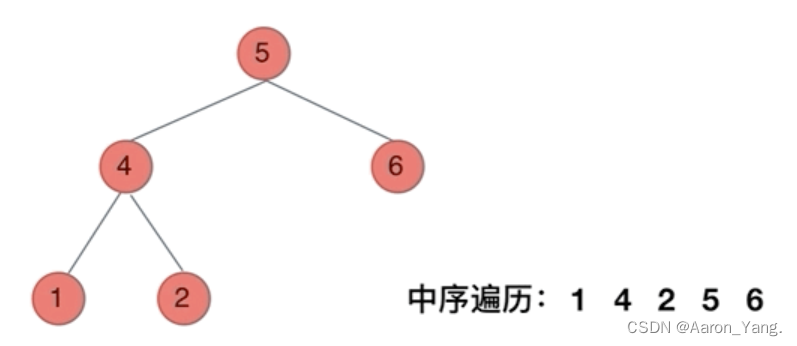
在这里插入图片描述

// 中序遍历顺序: 左-中-右 入栈顺序： 左-右
// 需要定义一个指针用于遍历二叉树
class Solution {public List<Integer> inorderTraversal(TreeNode root) {List<Integer> result = new ArrayList<>();if (root == null){return result;}Stack<TreeNode> stack = new Stack<>();TreeNode cur = root;while (cur != null || !stack.isEmpty()){// 一路向左，直到左孩子为空if (cur != null){stack.push(cur);cur = cur.left;}else{// 此时为空，就把当前栈里的节点给弹出// 栈顶的元素就是我们最近访问过的元素cur = stack.pop();result.add(cur.val);// 遍历右孩子，如果右孩子依旧为空的话，就回到else里，把当前节点给弹出cur = cur.right;}}return result;}
}