二叉树前序、中序遍历非递归实现
- 前序非递归遍历实现
- 中序非递归遍历实现
前序非递归遍历实现
题目: 二叉树前序遍历非递归实现
总体思路:用非递归的方式模拟递归遍历。
以下图为例:
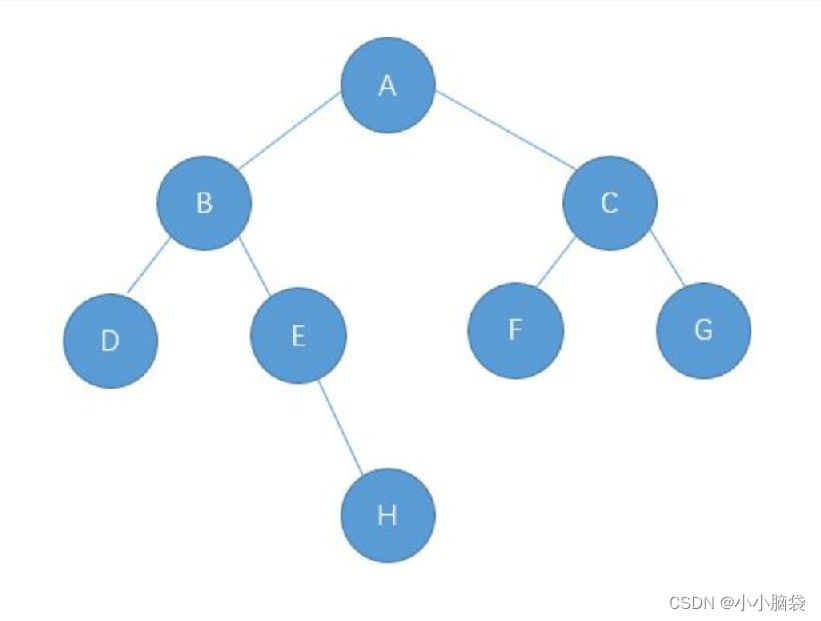
图示详解:

代码实现:
/*** Definition for a binary tree node.* public class TreeNode {* int val;* TreeNode left;* TreeNode right;* TreeNode() {}* TreeNode(int val) { this.val = val; }* TreeNode(int val, TreeNode left, TreeNode right) {* this.val = val;* this.left = left;* this.right = right;* }* }*/
class Solution {public List<Integer> preorderTraversal(TreeNode root) {List<Integer> list = new ArrayList<>();if(root == null){return list;}TreeNode cur = root;Stack<TreeNode> stack = new Stack<>();while(cur != null || stack.isEmpty() == false){//这个循环条件很难想到while(cur != null){stack.push(cur);list.add(cur.val);cur = cur.left;}//此时节点为空TreeNode top = stack.pop();cur = top.right;}return list;}
}
中序非递归遍历实现
题目: 二叉树中序遍历非递归实现
思路:中序非递归遍历和前序非递归遍历总体思路相同,唯一一个区别点是如果cur节点非空时,只压栈,list中并不立即记录当前cur的val值,同时令cur = cur.left。当cur == null时,栈顶元素出栈,此时在list中记录。如下以一组图示进行形象说明。

中序遍历和前序遍历代码处的不同只有一处,如下:

中序遍历非递归完整代码:
/*** Definition for a binary tree node.* public class TreeNode {* int val;* TreeNode left;* TreeNode right;* TreeNode() {}* TreeNode(int val) { this.val = val; }* TreeNode(int val, TreeNode left, TreeNode right) {* this.val = val;* this.left = left;* this.right = right;* }* }*/
class Solution {public List<Integer> inorderTraversal(TreeNode root) {List<Integer> list = new ArrayList<>();if(root == null){return list;}TreeNode cur = root;Stack<TreeNode> stack = new Stack<>();while(cur != null || stack.isEmpty() == false){//这个循环条件很难想到while(cur != null){stack.push(cur); cur = cur.left;}TreeNode top = stack.pop();list.add(top.val);cur = top.right;}return list;}
}
总结:前序、中序非递归遍历,两者只是在节点的记录时机不同,而节点的遍历路径完全相同。这也从根本上导致了两道题的AC代码几乎相同。




)


)





)

)



