题解：CF1920E. Counting Binary Strings

题意简述

题目链接：Problem - E - Codeforces。

洛谷翻译：Counting Binary Strings - 洛谷。

思路解析

假设我们有一个01串str（设里面有z个“1”），我们要求它里面有几个“好的串”。

我们不难想到，可以对它的每个元素“1”进行操作。为了方便描述，我们记s[i]为str中第i个元素“1”的前面直到离它最近的“1”之间0的数量加一。形象解释：其实就可以想象成把str分成若干份，每一份都是由前面的一堆“0”（可能没有）以及最后面的一个“1”（必须有）组成。特别的，我们记s[z+1]=1。那么很显然，对于第i个“1”，含有它的“好的串”（一定仅含有这一个“1”）的个数就是s[i]*s[i+1]，其中最长的长度就是s[i]+s[i+1]-1。（左端点的可能性就是s[i]的形象解释里的这几种，右端点就是s[i+1]的形象解释里每种情况向左侧移动一位）显然每个s[i]都大于等于1。

下面给一个例子。

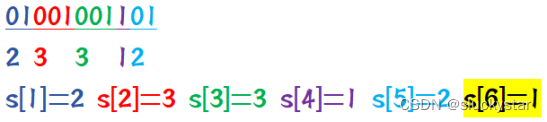
如上图，对于深蓝色的第一个“1”，含有它的“好的串”就有s[1]*s[2]=2*3=6个，其中左端点可以是str[1]、str[2]（深蓝色），右端点可以是str[3]、str[4]、str[5]（红色左移一位），总个数是乘法原理。

如上图，对于红色的第二个“1”，它所对应的“好的串”中最长的就是str[3~7]，它的长度很显然红色总数+绿色总数-1，即s[2]+s[3]-1。

不难证出，每一个s数组（定义如上）都能映射出一个str（01字符串）。于是，求出相应要求的字符串的数量就相当于求出对应的s的数量，这道题自然就变成了构造数组s。

我们在引入n和k。对于n，我们要保证，str子串中“好的串”的数量等于n，就相当于保证所有的s[i]*s[i+1]之和等于n；对于k，我们要保证，每一个“1”所在的“好的串”中最长的一个小于等于k，就相当于保证所有的s[i]+s[i+1]-1小于等于k。

于是题目就变成了求出满足上述条件的s的数量，我们自然而然想到DP。

状态：f[x][y]表示目前为止所有的s[i]*s[i+1]的和为i，最后一个s[i]为y，满足该条件的s的数量。

初值：f[0][x]=1。（如果一个数都没有，可以假设最前面的数是啥都行）

转移：f[x][y]=f[x-y*z][z]。（假设倒数第二个数为y，为了符合“n”的条件，上一次+y*z=x，所以上一次的总和是x-y*z；还有一个问题是z的范围，为了让它不越界，需保证x-y*z>=0，所以1≤z≤x/y，又需要满足“k”的要求，需保证y+z-1≤k，所以1≤z≤min(x/y,k+1-y)）

时间代价：遍历第一维——线性O(n)；遍历第二维——线性O(k)；遍历z——调和级数O(log(k))；总共O(nk*log(k))，完美通过。

代码展示

#include<bits/stdc++.h>
#define K 2750
#define N 2750
using namespace std;
const long long mod=998244353;
long long f[N][K]={};
int k=0,n=0,t=0;
int main(){scanf("%d",&t);while(t--){scanf("%d%d",&n,&k);for(int i=0;i<=n;i++){for(int j=1;j<=k;j++){f[i][j]=0;}}for(int i=1;i<=k;i++){f[0][i]=1;}for(int i=1;i<=n;i++){for(int j=1;j<=k;j++){for(int kk=1;kk<=min(i/j,k+1-j);kk++){f[i][j]=(f[i][j]+f[i-j*kk][kk])%mod;}}}long long ans=0;for(int i=1;i<=k;i++){ans=(ans+f[n][i])%mod;}printf("%lld\n",ans);}return 0;
}