考虑一个 2×2的矩阵A 和其逆矩阵A −1的情况：
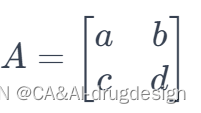
要求A的逆矩阵，首先计算A的行列式∣A∣：
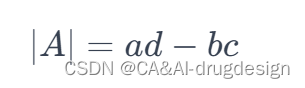
如果
∣A∣≠0, 则 A 可逆，逆矩阵 A −1的计算如下：
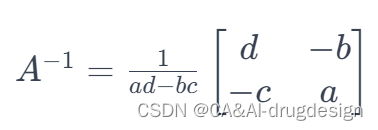
举例，考虑矩阵：
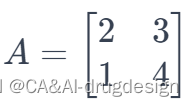
计算行列式
∣A∣=(2×4)−(3×1)=8−3=5
因为 ∣A∣≠0，所以 A 可逆。逆矩阵 A −1的计算如下：
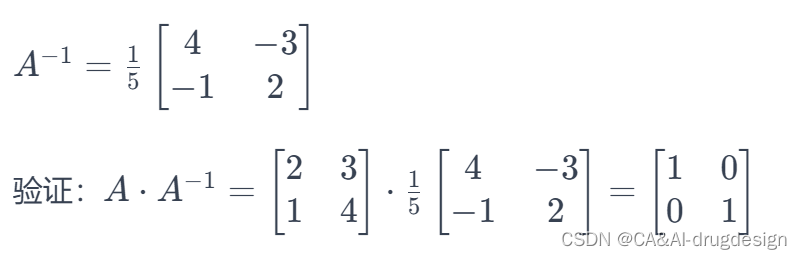
这证明了 A 与其逆矩阵相乘得到单位矩阵。
逆矩阵举例
本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.mzph.cn/news/641923.shtml
如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈email:809451989@qq.com，一经查实，立即删除！相关文章
精品基于Uniapp+springboot智慧校园管理系统App课程选课成绩
《[含文档PPT源码等]精品基于Uniappspringboot智慧校园管理系统App》该项目含有源码、文档、PPT、配套开发软件、软件安装教程、项目发布教程、包运行成功！
软件开发环境及开发工具：
开发语言：Java
后台框架：springboot、ssm
…
leaflet学习笔记-带过滤的图例（九）
前言
图例不只能够帮助我们在查看地图的时候更加方便容易地分辨不同颜色代表的要素，本文要介绍的图例组件还可以按需求过滤掉不用显示的要素，使地图的更能清晰的显示我们需要显示的内容
技术核心
说到过滤要素，第一时间想到的就是滑块组件…
一个大的rosbag数据包怎么分割成一个小的数据包？
文章目录 1. 按时间范围分割：2. 按照消息类型分割：3. 使用split命令：4. 使用Python脚本： 在ROS（机器人操作系统）中，
rosbag是一个用于记录和回放ROS主题消息的工具。如果你有一个大的
rosbag数…
![[C++] external “C“的作用和使用场景(案例)](https://img-blog.csdnimg.cn/direct/782e2ee080d9426b94f36df8feebadcd.png)
[C++] external “C“的作用和使用场景(案例)
C中extern "C"的作用是什么？
在 C 中，extern "C" 的作用是告诉编译器按照 C 语言的规范来处理函数名和变量名。这是因为 C 编译器会对函数名和变量名进行名称修饰(name mangling)，以区分不同的函数和变量。而在 C 语言中…
搭建互联网医疗平台：构建智慧医院APP的开发指南
本文将从技术层面出发，为大家提供构建互联网医疗平台、打造智慧医院APP的详细开发指南。
一、确定需求与功能
在开始开发之前，首先需要明确智慧医院APP的需求与功能。这包括患者预约挂号、在线咨询、病历查看、医疗报告查询等功能。 二、选择合适的开发…
安科瑞ARTM系列-无线测温解决方案
产品简介 温度在线监测主要是针对高低压开关柜内母排搭接点，断路器触头、电缆接头等电气连接点的温度进行监测，防止在运行过程中因氧化、松动、灰尘等因素造成接点接触电阻过大而发热成为隐患，温度在线监测能够提升设备安全保障，及…
宝塔面板优惠券(折扣券)领取入口及使用教程
宝塔面板是一款服务器管理软件，支持Linux与Windows系统，提供了丰富的功能和插件，让服务器管理变得更加简单、安全、高效。为了让更多用户体验到宝塔面板的便利，官方会不定期推出优惠券活动。本文将为大家详细介绍宝塔面板优惠券的…
ROS：rosdep与ROS2的安装记录
鱼香ROS一键安装：
一键安装微信使用指南 | 鱼香ROS rosdep安装： rosdep 是一个在ROS（Robot Operating System）生态系统中非常重要的工具，它用于安装ROS包的依赖项。rosdep 确保了ROS包所需的系统依赖项能够被正确安装…
MNIST 数据集详析：使用残差网络RESNET识别手写数字（文末送书）
MNIST 数据集已经是一个几乎每个初学者都会接触的数据集, 很多实验、很多模型都会以MNIST 数据集作为训练对象, 不过有些人可能对它还不是很了解, 那么今天我们一起来学习一下MNIST 数据集，同时构建残差网络来识别手写数字。 1.MNIST 介绍
MNIST手写数字数据库具有…
spring-framework6.x版本源码构建
6.x.修改gradle仓库构建
IDEA版本及gradle构建设置 在gradle指定仓库地址/wrapper/dists/找到与gradle wrapper相对应的gradle版本，在gradle的init.d/目录下新建init.gradle文件，内容如下：
allprojects{repositories {mavenLocal()maven { …
中仕教育：选调生和考研可以一起准备吗?
研究生入学考试，是本科生们提升学历继续深造的主要途径。而选调生，是指通过考试选拔的优秀应届毕业生，经过锻炼后分配到各级工作。这两者作为大部分人选择的方向，发展前景都是比较好的。
考研和选调生可以一起准备吗?
是可以的…
python+ctypes:ctypes调用so库
之前接到一个任务就是用python调用so库，也就是python调用cso库，也是第一次做这个，而且要的还很急，导致我也很忙碌，很多之前做的事请都丢下了。下面就介绍了ctypes调用so的简单例子。
ctypes 是 Python 的外部函数库。…
![[MySQL]关于表的增删改查](https://img-blog.csdnimg.cn/direct/5fe440b3e542430db6a084169a0c099d.png)
[MySQL]关于表的增删改查
目录
1.插入
1.1单行数据全列插入 1.2多行插入，指定列插入
编辑2.查询
2.1全列查询
2.2指定列查询
3.3查询字段为表达式 2.4别名
编辑2.5去重
2.6排序 2.7条件查询
2.7.1基本查询:
2.7.2 AND 和OR
2.7.3范围查询 2.7.4模糊查询 2.7.5分页查询 limit …
vue3 中组合键实现换行
vue3 中组合键实现换行
需求背景
有一个聊天室功能，采用输入框的形式，输入完毕使用Enter，可以直接进行发送。使用一些组合键 比如 commandEnter / shiftEnter / alt Enter … 可以实现换行操作。但现实的情况是，原生 Enter 天然…
【JavaEE Spring】MyBatis 操作数据库(基础操作)
MyBatis 操作数据库 本节目标前⾔JDBC 操作⽰例回顾1. 什么是MyBatis?2. MyBatis⼊⻔2.1 准备⼯作2.1.1 创建⼯程2.1.2 数据准备 2.2 配置数据库连接字符串2.3 写持久层代码2.4 单元测试 3. MyBatis的基础操作3.1 打印⽇志3.2 参数传递3.3 增(Insert)3.4 删(Delete)3.5 改(Upd…
太赞了！微信自动回复法宝，让沟通更高效！
如今，微信已成为人们生活和工作中不可或缺的一部分。然而，对于一些有多个微信账号的人说，常常会因为微信号太多，消息太多没能及时回复，或是客户咨询的问题很多都差不多，每次都要复制粘贴很是麻烦。
要想一…
记录yolov8_obb训练自己的数据集
一.数据集制作
1.标注软件：roLabelImg
roLabelImg是基于labelImg改进的，是用来标注为VOC格式的数据，但是在labelImg的基础上增加了能够使标注的框进行旋转的功能。 2.数据格式转换
2.1 xml转txt # 文件名称 ：roxml_to_dota.p…
Leetcode—40.组合总和II【中等】
2023每日刷题（七十七）
Leetcode—40.组合总和II 算法思想 实现代码
class Solution {
public:vector<vector<int>> combinationSum2(vector<int>& candidates, int target) {vector<vector<int>> ans;vector<int…
深度解析SD-WAN和混合WAN的网络方案区别
在企业网络的不断发展中，根据业务需要选择不同的广域网（WAN）解决方案显得至关重要。传统的基于传输控制协议/因特网协议（TCP/IP）的WAN是一种私有广域网，由企业网络和互联网服务提供商（ISP&#…
python222网站实战(SpringBoot+SpringSecurity+MybatisPlus+thymeleaf+layui)-热门标签推荐显示实现
锋哥原创的SpringbootLayui python222网站实战：
python222网站实战课程视频教程（SpringBootPython爬虫实战） ( 火爆连载更新中... )_哔哩哔哩_bilibilipython222网站实战课程视频教程（SpringBootPython爬虫实战） ( 火…
推荐文章
- 43.Textbox的数据绑定 C#例子 WPF例子
- 晨辉面试抽签和评分管理系统之七：面试成绩核算的三种方式
- 自定义注解使用AspectJ切面和SpringBoot的Even事件优雅记录业务接口及第三方接口调用日志实现思路
- 六种主流虚拟化技术全解析：OpenStack、KVM、Hyper-V、VMware、Xen及Docker
- 【Rust练习】28.use and pub
- vim使用指南
- Spring校验@RequestParams和@PathVariables参数
- VirtualBox 上安装Debian 后分辨率设置
- 服务器搭建－Linux基础知识
- 关于vue父子组件之间事件触发及数据传递问题
- ⛳ 面向对象面试题
- 实现仿简书选取内容生成分享图片效果