在信号处理和数学中，连续和离散是两种基本的表示方法，用于描述信号、函数或数据集。
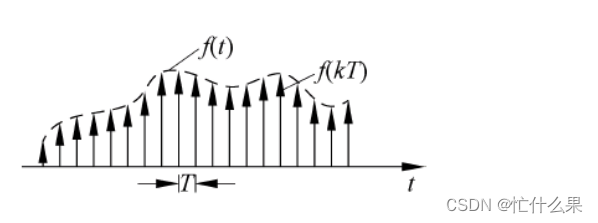对连续信号 f(t)进行等间隔采样得到

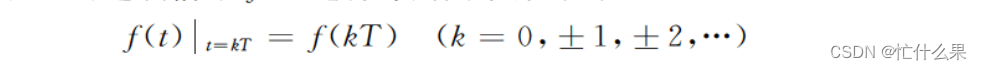
连续表示（Continuous Representation）

连续表示通常用于描述在一个连续范围内变化的信号或函数。在连续表示中，信号可以在任意时间点取值，这些值不受限于特定的时间间隔。

• 数学表示：连续信号通常用函数表示，例如 f(t)，其中t可以取任意实数值。
• 图形表示：连续信号在图表中通常表示为平滑的曲线。
• 应用示例：模拟信号、物理过程（如温度随时间的变化）、连续时间系统的响应。

离散表示（Discrete Representation）

离散表示用于描述仅在特定时间点或位置上定义的信号或数据集。在离散表示中，信号只在这些特定点上有值，而在其他时间或位置上没有定义。

• 数学表示：离散信号通常用一系列离散值表示，如 f[n]，其中 n是整数，代表序列中的索引。
• 图形表示：离散信号在图表中通常表示为一系列点或者垂直线条（柱状图）
• 应用示例：数字信号处理、数据采集系统中的样本、离散时间系统的响应。

连续与离散的转换

采样：将连续信号转换为离散信号的过程称为采样。

• 例如，模拟-数字转换器（ADC）会在连续时间信号上进行采样，生成离散时间信号。

插值和重建：从离散信号重建或近似连续信号的过程称为插值。

• 例如，数字-模拟转换器（DAC）会使用插值方法从离散信号中重建模拟信号。

这两种表示方式在信号处理、通信和控制系统等领域都非常重要，各自有其独特的应用和处理方法。