目录

1. 二进制求和（简单）

2. 两数相加（中等）

3. 两数相除（中等）

4. 字符串相乘（中等）

---

1. 二进制求和（简单）

从字符串的右端出发向左做加法，逢二进一。

class Solution {
public:string addBinary(string a, string b) {string ans;int i = a.size() - 1; // a的下标是从0到iint j = b.size() - 1; // b的下标是从0到jint carry = 0 ; // 进位while (i >= 0 || j >= 0){int digitA = i >= 0 ? a[i--] - '0' : 0;int digitB = j >= 0 ? b[j--] - '0' : 0;int sum = digitA + digitB + carry;carry = sum >= 2 ? 1 : 0;sum = sum >= 2 ? sum - 2 : sum;ans += sum + '0';}if (carry){ans += '1';}reverse(ans.begin(), ans.end());return ans;}
};

2. 两数相加（中等）

class Solution {
public:ListNode* addTwoNumbers(ListNode* l1, ListNode* l2) {ListNode* preHead = new ListNode; // 哨兵节点ListNode* tail = preHead;int carry = 0; // 进位while (l1 || l2){int n1 = l1 ? l1->val: 0;int n2 = l2 ? l2->val: 0;int sum = n1 + n2 + carry;tail->next = new ListNode(sum % 10);carry = sum / 10;tail = tail->next;if (l1){l1 = l1->next;}if (l2){l2 = l2->next;}}if (carry){tail->next = new ListNode(carry);}return preHead->next;}
};

3. 两数相除（中等）

假设被除数是a，除数是b。

如果a、b都是正数，且a>=b

a最多大于b的2^k倍，将a减去b的2^k倍，剩下的被除数再重复这样的操作，直到a < b

以22除以3为例：

22最多大于3的4倍：22 - 3 * 4 = 10

10最多大于3的2倍：10 - 3 * 2 = 4

4最多大于3的1倍： 4 - 3 * 1 = 1

商是4 + 2 + 1 = 7，余数是1

如果a、b都是负数，且a <= b

a最多小于b的2^k倍，将a减去b的2^k倍，剩下的被除数再重复这样的操作，直到a > b

以-22除以-3为例：

-22最多小于-3的4倍：-22 - (-3) * 4 = -10

-10最多小于-3的2倍：-10 - (-3) * 2 = -4

-4最多小于-3的1倍： -4 - (-3) * 1 = -1

商是4 + 2 + 1 = 7，余数是-1

class Solution {
public:int divide(int dividend, int divisor) {// -2^31/-1=2^31 溢出if (dividend == INT_MIN){if (divisor == -1){return INT_MAX;}else if (divisor == 1){return INT_MIN;}}// 全部转化为负数，如果全部转化为正数，-2^31转化为正数会溢出int negative = 2; // 表示被除数和除数有几个是负数if (dividend > 0){dividend = -dividend;negative--;}if (divisor > 0){divisor = -divisor;negative--;}int result = divideCore(dividend, divisor);return negative == 1 ? -result : result;}private:int divideCore(int a, int b){int result = 0;while (a <= b){int k = 1;int val = b; // val表示b的2^k倍while (val >= INT_MIN / 2 && a <= val + val){k += k;val += val;}result += k;a -= val;}return result;}
};

4. 字符串相乘（中等）

无进位相乘后相加，再处理进位。

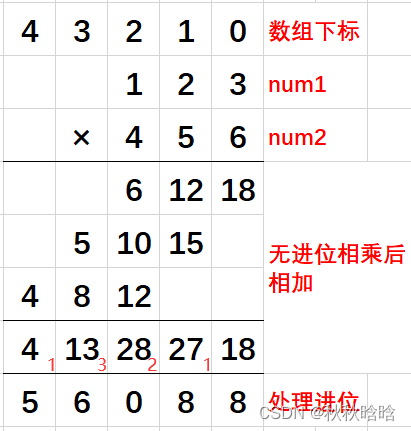
class Solution {
public:string multiply(string num1, string num2) {if (num1 == "0" || num2 == "0")return "0";int n1 = num1.size();int n2 = num2.size();reverse(num1.begin(), num1.end());reverse(num2.begin(), num2.end());vector<int> sums(n1 + n2 -1);// 无进位相乘后相加for (int i = 0; i < n2; i++){for (int j = 0; j < n1; j++){sums[i + j] += (num2[i] - '0') * (num1[j] - '0');}}// 处理进位string ans;int i = 0;int carry = 0;while (i < n1 + n2 -1){int sum = sums[i++] + carry;ans += sum % 10 + '0';carry = sum / 10;}if (carry){ans += carry + '0';}// 反转reverse(ans.begin(), ans.end());return ans;}
};