第五部分、数组和广义表详解

数组和广义表,都用于存储逻辑关系为“一对一”的数据。
数组存储结构,99% 的编程语言都包含的存储结构,用于存储不可再分的单一数据;而广义表不同,它还可以存储子广义表。
本章重点从矩阵的角度讨论二维数组的存储,同时讲解广义表的存储结构以及有关其广度和深度的算法实现。
三、矩阵(稀疏矩阵)压缩存储(3种方式)
数据结构中,提供针对某些特殊矩阵的压缩存储结构。
这里所说的特殊矩阵,主要分为以下两类:
- 含有大量相同数据元素的矩阵,比如对称矩阵;
- 含有大量 0 元素的矩阵,比如稀疏矩阵、上(下)三角矩阵;
针对以上两类矩阵,数据结构的压缩存储思想是:矩阵中的相同数据元素(包括元素 0)只存储一个。
1、对称矩阵
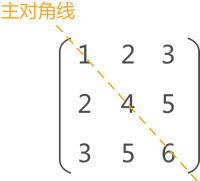
图 1 对称矩阵示意图
图 1 的矩阵中,数据元素沿主对角线对应相等,这类矩阵称为对称矩阵。
矩阵中有两条对角线,其中图 1 中的对角线称为主对角线,另一条从左下角到右上角的对角线为副对角线。对称矩阵指的是各数据元素沿主对角线对称的矩阵。
结合数据结构压缩存储的思想,我们可以使用一维数组存储对称矩阵。由于矩阵中沿对角线两侧的数据相等,因此数组中只需存储对角线一侧(包含对角线)的数据即可。
对称矩阵的实现过程是,若存储下三角中的元素,只需将各元素所在的行标 i 和列标 j 代入下面的公式:
![]()
存储上三角的元素要将各元素的行标 i 和列标 j 代入另一个公式:
![]()
最终求得的 k 值即为该元素存储到数组中的位置(矩阵中元素的行标和列标都从 1 开始)。
例如,在数组 skr[6] 中存储图 1 中的对称矩阵,则矩阵的压缩存储状态如图 3 所示(存储上三角和下三角的结果相同):

图 3 对称矩阵的压缩存储示意图
注意,以上两个公式既是用来存储矩阵中元素的,也用来从数组中提取矩阵相应位置的元素。例如,如果想从图 3 中的数组提取矩阵中位于 (3,1) 处的元素,由于该元素位于下三角,需用下三角公式获取元素在数组中的位置,即:
![]()
结合图 3,数组下标为 3 的位置存储的是元素 3,与图 1 对应。
2、上(下)三角矩阵
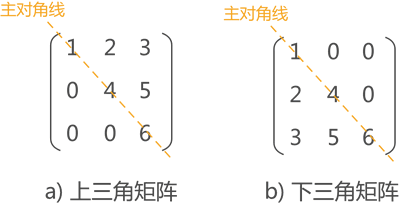
图 4 上(下)三角矩阵
如图 4 所示,主对角线下的数据元素全部相同的矩阵为上三角矩阵(图 4a)),主对角线上元素全部相同的矩阵为下三角矩阵(图 4b))。
对于这类特殊的矩阵,压缩存储的方式是:上(下)三角矩阵采用对称矩阵的方式存储上(下)三角的数据(元素 0 不用存储)。
例如,压缩存储图 4a) 中的上三角矩阵,矩阵最终的存储状态同图 3 相同。因此可以得出这样一个结论,上(下)三角矩阵存储元素和提取元素的过程和对称矩阵相同。
3、稀疏矩阵
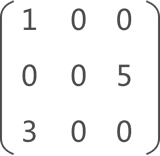
图 5 稀疏矩阵示意图
如图 5 所示,如果矩阵中分布有大量的元素 0,即非 0 元素非常少,这类矩阵称为稀疏矩阵。
压缩存储稀疏矩阵的方法是:只存储矩阵中的非 0 元素,与前面的存储方法不同,稀疏矩阵非 0 元素的存储需同时存储该元素所在矩阵中的行标和列标。
例如,存储图 5 中的稀疏矩阵,需存储以下信息:
- (1,1,1):数据元素为 1,在矩阵中的位置为 (1,1);
- (3,3,1):数据元素为 3,在矩阵中的位置为 (3,1);
- (5,2,3):数据元素为 5,在矩阵中的位置为 (2,3);
- 除此之外,还要存储矩阵的行数 3 和列数 3;
由此,可以成功存储一个稀疏矩阵。
注意,以上 3 种特殊矩阵的压缩存储,除了将数据元素存储起来,还要存储矩阵的行数值和列数值,具体的实现方式后续会介绍 3 种,本节仅需了解矩阵压缩存储的原理。
4、矩阵压缩存储的 3 种方式
对于以上 3 种特殊的矩阵,对阵矩阵和上下三角矩阵的实现方法是相同的,且实现过程比较容易,仅需套用上面给出的公式即可。
稀疏矩阵的压缩存储,数据结构提供有 3 种具体实现方式:
- 三元组顺序表;
- 行逻辑链接的顺序表;
- 十字链表;
稀疏矩阵的三种存储结构,会利用后续的 3 篇文章做重点介绍。
四、三元组顺序表,稀疏矩阵的三元组表示及(C语言)实现
本节介绍稀疏矩阵的三元组顺序表压缩存储方式。
通过《矩阵的压缩存储》一节我们知道,稀疏矩阵的压缩存储,至少需要存储以下信息:
- 矩阵中各非 0 元素的值,以及所在矩阵中的行标和列标;
- 矩阵的总行数和总列数;
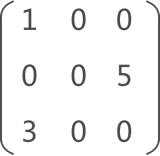
图 1 稀疏矩阵示意图
例如,图 1 是一个稀疏矩阵,若对其进行压缩存储,矩阵中各非 0 元素的存储状态如图 2 所示:

图 2 稀疏矩阵的压缩存储示意图
图 2 的数组中,存储的是三元组(即由 3 部分数据组成的集合),组中数据分别表示(行标,列标,元素值)。
注意,这里矩阵的行标和列标都从 1 开始。
C 语言中,三元组需要用结构体实现,如下所示:
//三元组结构体
typedef struct {
int i,j;//行标i,列标j
int data;//元素值
}triple;
由于稀疏矩阵中非 0 元素有多个,因此需要建立 triple 数组存储各个元素的三元组。除此之外,考虑到还要存储矩阵的总行数和总列数,因此可以采用以下结构表示整个稀疏矩阵:
#define number 20
//矩阵的结构表示
typedef struct {
triple data[number];//存储该矩阵中所有非0元素的三元组
int n,m,num;//n和m分别记录矩阵的行数和列数,num记录矩阵中所有的非0元素的个数
}TSMatrix;
可以看到,TSMatrix 是一个结构体,其包含一个三元组数组,以及用于存储矩阵总行数、总列数和非 0 元素个数的变量。
假设采用 TSMatrix 结构体存储图 1 中的稀疏矩阵,其 C 语言实现代码应该为:
#include<stdio.h>
#define number 3
typedef struct {
int i,j;
int data;
}triple;
typedef struct {
triple data[number];
int n,m,num;
}TSMatrix;
//输出存储的稀疏矩阵
void display(TSMatrix M);
int main() {
TSMatrix M;
M.m=3;
M.n=3;
M.num=3;
M.data[0].i=1;
M.data[0].j=1;
M.data[0].data=1;
M.data[1].i=2;
M.data[1].j=3;
M.data[1].data=5;
M.data[2].i=3;
M.data[2].j=1;
M.data[2].data=3;
display(M);
return 0;
}
void display(TSMatrix M){
for(int i=1;i<=M.n;i++){
for(int j=1;j<=M.m;j++){
int value =0;
for(int k=0;k<M.num;k++){
if(i == M.data[k].i && j == M.data[k].j){
printf("%d ",M.data[k].data);
value =1;
break;
}
}
if(value == 0)
printf("0 ");
}
printf("\n");
}
}
输出结果为:
1 0 0
0 0 5
3 0 0


![[python语言]数据类型](http://pic.xiahunao.cn/[python语言]数据类型)



时找不到根目录的解决办法)
----声明变量)











