机器学习笔记

机器学习系列笔记，主要参考李航的《机器学习方法》，见参考资料。
第一章 机器学习简介
第二章 感知机
第三章 支持向量机
第四章 朴素贝叶斯分类器
第五章 Logistic回归
第六章 线性回归和岭回归
第七章 多层感知机与反向传播【Python实例】
第八章 主成分分析【PCA降维】
第九章 隐马尔可夫模型
第十章 奇异值分解

---

奇异值分解（Singular Value Decomposition）是线性代数中一种重要的矩阵分解，奇异值分解则是特征分解在任意矩阵上的推广。在信号处理、统计学等领域有重要应用。奇异值分解在统计中的主要应用为主成分分析（PCA），PCA算法的作用是把数据集映射到低维空间中去。 数据集的特征值（在SVD中用奇异值表征）按照重要性排列，降维的过程就是舍弃不重要的特征向量的过程，而剩下的特征向量组成的空间即为降维后的空间。

一、矩阵的基本子空间

对非零矩阵$A\in {\mathbb{R}}^{m\times n}$,其秩 rank$(A)=r$ , r ≤ min ⁡ { m , n } . r\leq\min\{m,n\}. r≤min{m,n}. $A$的四个基本子空间：

1. $A$的列空间（$A$的值域）：
   R ( A ) = { z ∈ R m ∣ ∃ x ∈ R n , z = A x } R(A)=\{z\in\mathbb{R}^m|\exists x\in\mathbb{R}^n,z=Ax\} R(A)={z∈Rm∣∃x∈Rn,z=Ax}
2. $A$的零空间：
   N ( A ) = { x ∈ R n ∣ A x = 0 } . N(A)=\{x\in\mathbb{R}^n|Ax=0\}. N(A)={x∈Rn∣Ax=0}.
3. $A$的行空间（$A^T$的值域）：
   R ( A T ) = { y ∈ R n ∣ ∃ x ∈ R m , y = A T x } R(A^T)=\{y\in\mathbb{R}^n|\exists x\in\mathbb{R}^m,y=A^Tx\} R(AT)={y∈Rn∣∃x∈Rm,y=ATx}
4. $A$的左零空间（$A^T$的零空间)：

N ( A T ) = { x ∈ R m ∣ A T x = 0 } . N(A^T)=\{x\in\mathbb{R}^m|A^Tx=0\}. N(AT)={x∈Rm∣ATx=0}.

四个子空间的关系如下图所示:

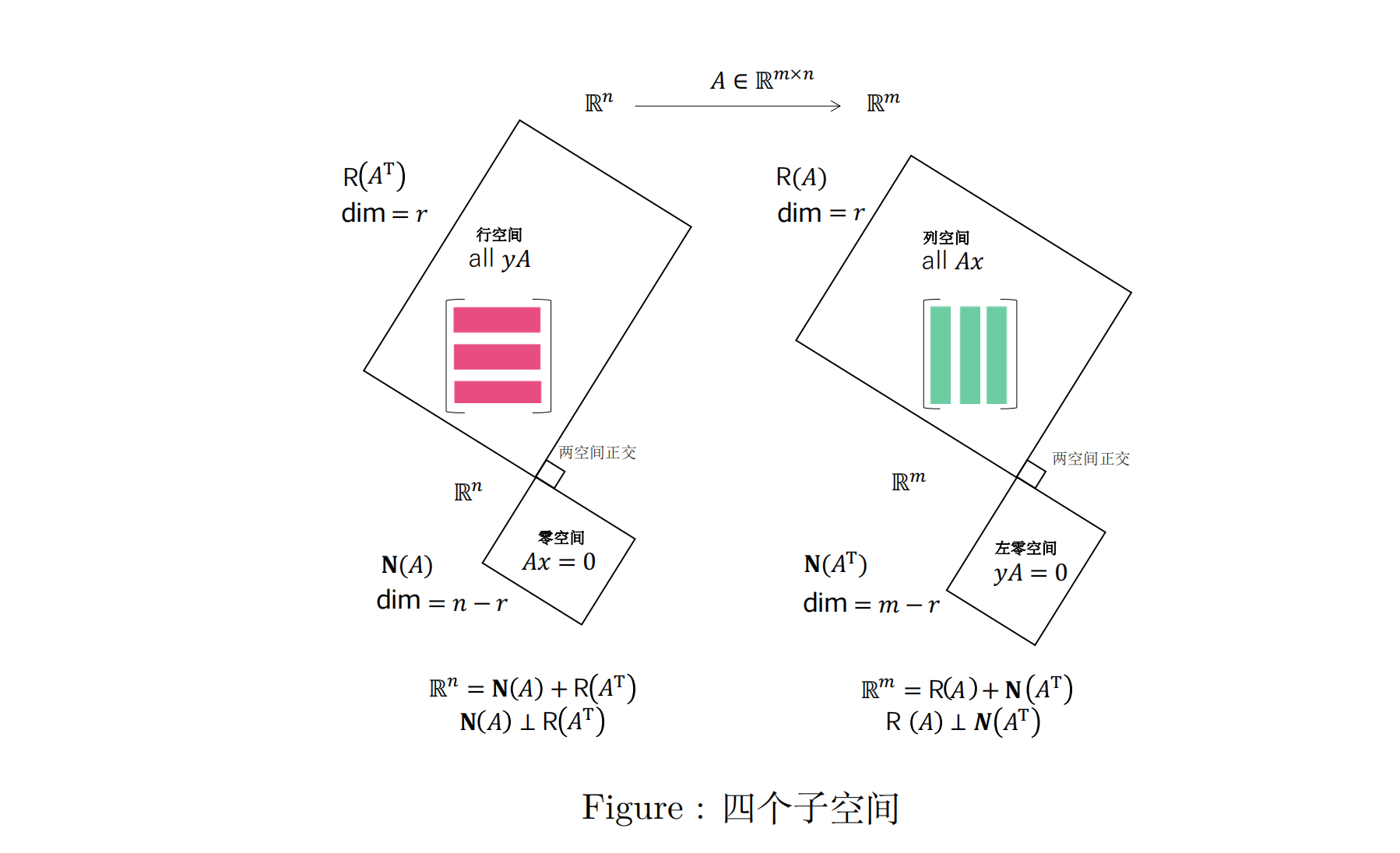
我们证明其中两条:

• $R(A)\perp N(A^{\mathrm{T}})$

证明：

$\forall z\in R(A),y\in N(A^T)$，有
$$<z,y>=z^{T}y=(Ax{)}^{T}y=x^T{A}^{T}y=0$$
所以$z\perp y$，证毕.

• $\dim (R(A))+\dim (N(A))=n$（秩零定理）

证明：

矩阵A的零空间就Ax=0的解的集合，则零空间的维数为n-r。因为秩为r，则自由变量的个数为n-r，有几个自由变量，零空间就可以表示成几个特解的线性组合，也即是零空间的维数为自由变量的个数。

二、舒尔分解

在介绍奇异值分解之前，我们首先介绍一下Schur分解，利用Schur分解，可以导出奇异值分解.

Schur decomposition

For each $A\in {\mathbb{C}}^{n\times n}$ with eigenvalue${\lambda }_1,{\lambda }_2,\cdots ,{\lambda }_n$ in any prescribed order，there exist unitary matrix $U\in C^{n\times n}s.t.T=U^{\ast }AU$ is an upper triangle matrix with diagonal entries $t_{ii}={\lambda }_i$:
$$T=[\begin{array}{cccc}{\lambda }_1& t_{12}& \cdots & t_{1n}\\ 0& {\lambda }_2& \cdots & ⋮\\ 0& \cdots & {\lambda }_{n-1}& t_{n-n}\\ 0& \cdots & \cdots & {\lambda }_n\end{array}].$$

• 也就是说Hermitian矩阵的Schur分解其实就是特征值分解.
• Hermitian矩阵一定可以进行对角化.（实对称矩阵也一定可以对角化)

三、奇异值分解

（1）定义

（2）证明

因为$A\in {\mathbb{R}}^{m\times n}$（不妨设$m>n$，且$\mathrm{rank}(A)=r$），所以$A^{T}A$和$A{A}^T$都是对称的实矩阵，我们以$A^{T}A$为例，由Schur分解知，一定存在正交矩阵$V\in {\mathbb{R}}^{n\times n}$，使得：
$$V^T{A}^{T}AV=\Lambda =\mathrm{diag}({\lambda }_1,{\lambda }_2,\cdots ,{\lambda }_n)={\Sigma }^T\Sigma$$其中${\lambda }_1\ge {\lambda }_2\ge \cdots {\lambda }_n\ge 0$，此时矩阵$V$我们已经有了，就是$A^{T}A$的特征向量矩阵，那么如何构造$U$呢？我们首先给出一个引理：

$$\mathrm{rank}(A^{T}A)=\mathrm{rank}(A)=r.$$

证明：设$x\in {\mathbb{R}}^n$,则
$$Ax=0\Rightarrow A^{T}Ax=0;$$
反之，
$$A^{T}Ax=0\Rightarrow x^T{A}^{T}Ax=0\Rightarrow \parallel Ax{\parallel }_2^2=0\Rightarrow Ax=0.$$
$A^{T}A$和$A$的零空间相同，因此$\mathrm{rank}(A^{T}A)=\mathrm{rank}(A)=r.$

由$\mathrm{rank}(A^{T}A)=\mathrm{rank}(A)=r$，则
$$\begin{gathered} {\lambda }_1\ge {\lambda }_2\ge \cdots \ge {\lambda }_r>0, \\ {\lambda }_{r+1}=\cdots ={\lambda }_n=0. \end{gathered}$$
我们将$V$分成两部分$V=[V_1,V_2]$,其中 $V_1=[v_1,\cdots ,v_r]$, $V_2=[v_{r+1},\cdots ,v_n].$

• $v_{r+1},\cdots ,v_n$正好构成$A^{T}A$的零空间$N(A^{T}A)($也是$N(A))$的一组标准正交基.
• $A{V}_2=0.$
• $I=V{V}^T=V_1{V}_1^T+V_2{V}_2^T.$
• $A=AI=A(V_1{V}_1^T+V_2{V}_2^T)=A{V}_1{V}_1^T.$

同样的我们将$U$分为两部分$U=[U_1,U_2]$，考察 $AV=U\Sigma$:
$$\begin{array}{rl}& A\left[\begin{array}{lllc}{v}_1& \dots & v_r& \dots v_n\end{array}\right]=\left[\begin{array}{lll}{u}_1& \cdots & u_m\end{array}\right]\left[\begin{array}{ccc}{\sigma }_1& 0& \\ \cdots & {\sigma }_r& \\ 0& & 0\end{array}\right]\\ & A{v}_1={\sigma }_1{u}_1\Rightarrow u_1=\frac{A{v}_1}{{\sigma }_1}\left({\sigma }_1\ne 0\right).\end{array}$$
若${\sigma }_1\dots {\sigma }_r\ne 0$，则有：
$$u_i=\frac{A{v}_i}{{\sigma }_i},i=1,2\cdots ,r.$$于是我们从$V_1=[v_1,v_2,\cdots ,v_r]$出发，构造$U_1=[u_1,\cdots ,u_r]$如下：
$$u_i=\frac{1}{\sqrt{{\lambda }_i}}A{v}_i,i=1,\cdots ,r.$$
下面验证$U_1$中的列向量是否正交：

$$u_i^T{u}_j=\frac{1}{\sqrt{{\lambda }_i{\lambda }_j}}{v}_i^T{A}^{T}A{v}_j=\frac{1}{\sqrt{{\lambda }_i{\lambda }_j}}{v}_i^T{\lambda }_j{v}_j={\delta }_{ij}=\{\begin{array}{l}1,i=j\\ 0,i\ne j.\end{array}$$

这说明
$$[u_1,\cdots ,u_r]$$
是$A$的列空间$R(A)$的一组标准正交基.接着我们构造$U_2$，补全$U=[U_1,U_2]$.我们知道$R(A)$的正交补空间为 $N(A^T)$，设$u_{r+1},\cdots ,u_m$为$N(A^T)$的一组标准正交基.令
$$U_2=[u_{r+1},\cdots ,u_m]$$那么此时$U=[U_1,U_2]$为正交矩阵，整个$U$我们就都得到了！

（3）与四大子空间的关系

再来观察:
$$A[V_1,V_2]=[U_1,U2]\Sigma$$
由上面的证明过程我们知道：

1. $V_1$是$R(A^T)$的一组基，$V_2$是$N(A)$的一组基.
2. $U_1$是$R(A)$的一组基，$U2$是$N(A^T)$的一组基.

矩阵A的奇异值分解的左右奇异向量刚好是$A$的四大基本子空间的基！

（4）推论

由$A=U\Sigma V^T$可推出

• $A^{T}A=V({\Sigma }^T\Sigma )V^T$，右奇异向量为$A^{T}A$的特征向量.
• $A{A}^T=U(\Sigma {\Sigma }^T)U^T$，左奇异向量为$A{A}^T$的特征向量.
• $A$的奇异值${\sigma }_1,\cdots ,{\sigma }_n$是唯一的，但$U$和$V$不唯一.
• 矩阵的奇异值分解可以看作将其对应的线性变换分解为旋转变换$(V^T)$、伸缩变换$(\Sigma )$及旋转变换$(U)$的组合.

四、矩阵近似

奇异值分解的一个应用是低秩矩阵估计，在F范数最小意义下，可以用秩为k(k<r)的低秩矩阵对A进行近似.

（1）低秩矩阵估计

下面首先给出紧奇异值分解和截断奇异值分解的概念：

这里我们采用$F$范数(参考我的这篇文章：范数）来刻画两个矩阵$A$和$X$的差异：$\Vert A-X{\Vert }_F$，下面我们通过定理2会知道，在$F$范数的意义下，截断奇异值分解就是秩不超过$k$的矩阵中对$A$的最好的近似.

引理1

设$A\in {\mathbb{R}}^{m\times n}$的奇异值分解为$U\Sigma V^T$,其中$\Sigma =$diag$({\sigma }_1,\cdots ,{\sigma }_n)$ ，则：
$$\parallel A{\parallel }_F=\sqrt{\sum _{i=1}^n{\sigma }_i^2}$$
证明：$\Vert A{\Vert }_F=\Vert U\Sigma V^T{\Vert }_F=\Vert \Sigma {\Vert }_F=\sqrt{{\sum }_{i=1}^n{\sigma }_i^2}.$

引理2

设$A\in {\mathbb{R}}^{m\times n}$ 且$\mathrm{rank}(A)=r$,并设$M$为${\mathbb{R}}^{m\times n}$中所有秩不超过$k$的矩阵集合，$0<k<r$,则存在一个秩为$k$的矩阵$X$,使得：
$$\Vert A-X{\Vert }_F=\underset{S\in \mathcal{M}}{\min }\Vert A-S{\Vert }_F.$$
称矩阵$X$为矩阵$A$在Frobenius范数意义下的最优近似.

• 上述定理说明在秩不超过$k$的$m\times n$矩阵集合中，存在矩阵$A$的最优近似矩阵$X$；
• $A^{\prime }=U{\Sigma }^{\prime }{V}^T$就是这样的最优近似矩阵.
• $A$的紧奇异值分解是在Frobenius范数意义下$A$的无损压缩.
• $A$的秩为$k$的截断奇异值分解是A的有损压缩，通常$k$远小于$r$, 因此是由低秩矩阵实现了对$A$的压缩。

（2）矩阵的外积展开

设$A\in {\mathbb{R}}^{m\times n}$且 其奇异值分解为$U\Sigma V^T$,则

$$\begin{array}{rl}A& =U\Sigma V^T\\ & =[{\sigma }_1{u}_1,\cdots ,{\sigma }_n{u}_n]\left[\begin{array}{l}{v}_1^T\\ ⋮\\ v_n^T\end{array}\right]\\ & ={\sigma }_1{u}_1{v}_1^T+\cdots +{\sigma }_n{u}_n{v}_n^T.\end{array}$$
称$A={\sigma }_1{u}_1{v}_1^T+\cdots +{\sigma }_n{u}_n{v}_n^T$为$A$的外积展开式. 令
$$A_k=\sum _{i=1}^k{\sigma }_i{u}_i{v}_i^T$$
则$A_k$的秩为$k$, 是$A$的截断奇异值分解，$A_k$是秩为$k$的矩阵中在F范数意义下$A$的最优近似矩阵.

参考资料

1. 李航. 机器学习方法. 清华大学出版社, 2022.