问题描述

最长公共子序列(Longest Common Subsequence，LCS)即求两个序列最长的公共子序列(可以不连续)。比如3 2 1 4 5和1 2 3 4 5两个序列，最长公共子序列为2 4 5 长度为3。解决这个问题必然要使用动态规划。既然要用到动态规划，就要知道状态转移方程。我们令L[i][j] 表示序列 A 和序列 B 的最长公共子序列的长度，则状态转移方程如下：
若a[i]=b[j]， 则 L[i][j]=L[i-1][j-1] +1
若a[i]!=b[j]， 则 L[i][j]=max (L[i][j-1]，L[i-1][j]）
即：相同的取左上加1,不同取上和左中的最大值

package com.algorithm;
/*** long common Subseq*/
public class LCS {public static void main(String[] args) {char[] seq1 = new char[]{'a','b','d','c','b','a','b'};char[] seq2 = new char[]{'b','d','c','b','a','b','b'};int[][] dp = new int[seq1.length + 1][seq2.length + 1];//存储两个序列当前i和j的公共序列长度，多存储一位是空字符，默认都市0//初始化for (int i = 0; i < seq1.length + 1; i++) {dp[i][0] = 0;}for (int j = 0; j < seq2.length + 1; j++) {dp[0][j] = 0;}//计算dp,相同的取左上加1,不同取上和左中的最大值for(int i = 1; i < seq1.length; i++) {for(int j = 1; j<seq2.length; j++) {if(seq1[i] == seq2[j]) {dp[i][j] = dp[i-1][j-1]+1; //左上加1} else {dp[i][j] = Math.max(dp[i][j-1],dp[i-1][j]); //上和左中的最大值}}}//获取最长公共子序列长度，也就是dp中最大的那个值int max = 0;for(int i = 1; i < dp.length; i++) {for (int j = 1; j < dp.length; j++) {max = Math.max(max, dp[i][j]);}}System.out.println("long common seq size:"+max);}
}

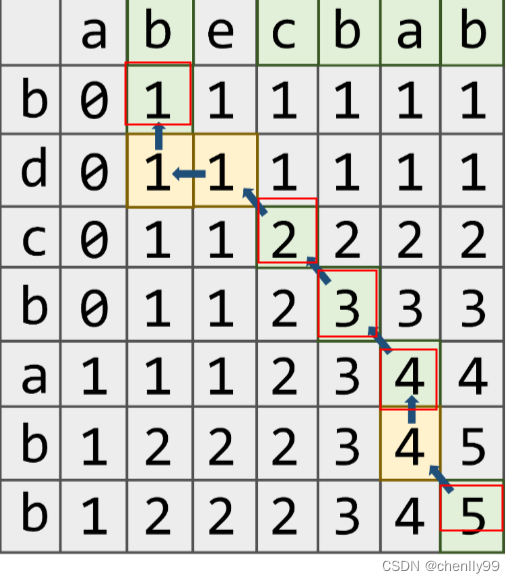
从右下角开始，如果有dp[i][j]==dp[i-1][j-1]+1则往左上走一格。得到整个子序列的求解过程。b,c,b,a,b