题目
给定一个 正整数 数组 beans ,其中每个整数表示一个袋子里装的魔法豆的数目。
请你从每个袋子中 拿出 一些豆子(也可以 不拿出),使得剩下的 非空 袋子中(即 至少还有一颗 魔法豆的袋子)魔法豆的数目 相等。一旦把魔法豆从袋子中取出,你不能再将它放到任何袋子中。
请返回你需要拿出魔法豆的 最少数目。
示例 1:
输入:beans = [4,1,6,5]
输出:4
解释:
- 我们从有 1 个魔法豆的袋子中拿出 1 颗魔法豆。剩下袋子中魔法豆的数目为:[4,0,6,5]
- 然后我们从有 6 个魔法豆的袋子中拿出 2 个魔法豆。剩下袋子中魔法豆的数目为:[4,0,4,5]
- 然后我们从有 5 个魔法豆的袋子中拿出 1 个魔法豆。剩下袋子中魔法豆的数目为:[4,0,4,4]
总共拿出了 1 + 2 + 1 = 4 个魔法豆,剩下非空袋子中魔法豆的数目相等。
没有比取出 4 个魔法豆更少的方案。
示例 2:
输入:beans = [2,10,3,2]
输出:7
解释:
- 我们从有 2 个魔法豆的其中一个袋子中拿出 2 个魔法豆。剩下袋子中魔法豆的数目为:[0,10,3,2]
- 然后我们从另一个有 2 个魔法豆的袋子中拿出 2 个魔法豆。剩下袋子中魔法豆的数目为:[0,10,3,0]
- 然后我们从有 3 个魔法豆的袋子中拿出 3 个魔法豆。剩下袋子中魔法豆的数目为:[0,10,0,0]
总共拿出了 2 + 2 + 3 = 7 个魔法豆,剩下非空袋子中魔法豆的数目相等。
没有比取出 7 个魔法豆更少的方案。
提示:
- 1 <= beans.length <= 10^5
- 1 <= beans[i] <= 10^5
解法1
分析
- 从题目和示例中我们可以得到目标数组当中只会有两种元素,一个是0,一个是x。
- 我们只能拿出豆子,并不能加入豆子。所以对于beans[i]的变化,只能是减小或者不变。
- 假设将beans排序,我们依次选择beans[i]为x,那么beans[i]及其以后的所有值都是得缩减为x。
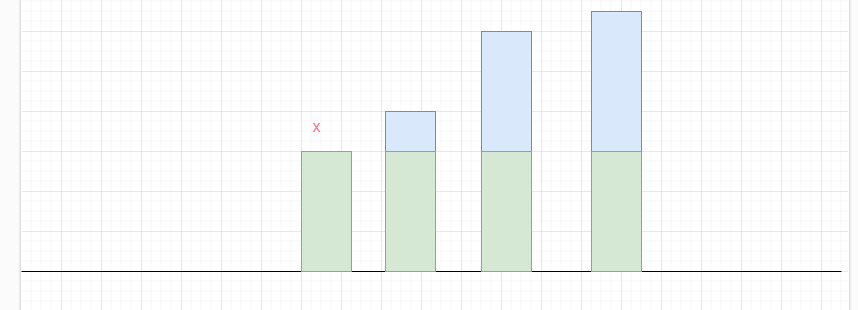
并且beans[i]前面的元素都是0。 - 此时数组的和为sum = **(n-i)*beans[i],**我们需要拿出最少的魔法豆,即需要sum值最大。
- 循环依次求解最大的sum即可。
- 拿出的魔法都数量就等于total-sum,total原本的魔法豆总和。
代码
public long minimumRemoval(int[] beans) {Arrays.sort(beans);int total = 0;for (int bean : beans) {total+=bean;//求和}long sum = -1;//求出剩余的豆子的最大总和for (int i = 0; i < beans.length; i++) {sum = Math.max(sum,(long) (beans.length-i)*beans[i]);}return total-max;//返回需要拿出豆子的最小数量。
}
复杂度
时间复杂度:O(f(x))=nlogn
核心语句执行次数:f(x) = nlogn(排序)+n(查找sum最大值)
空间复杂度:O(1)
解法2
根据提示,我们可以知道数组中元素的最大值不超过10^5,所以我们完全可以用hash来代替排序,进一步降低时间复杂度
hash之后,下标i就是原来的数组里面的值。
顺序即原始下标,就是hash数组的前缀和。用变量count记录。
public long minimumRemoval(int[] beans) {int [] hash = new int[100001];long total = 0;for (int bean : beans) {hash[bean]++;total+=bean;}long sum = -1;int count = 0;for (int i = 1; i < 100001; i++) {if(hash[i]!=0){sum = Math.max(sum,(long) (beans.length-count)*i);count+=hash[i];}}return total-max;}
时间复杂度:O(maxVal)在这里近似O(n)
空间复杂度:O(maxVal)在本题近似O(n)
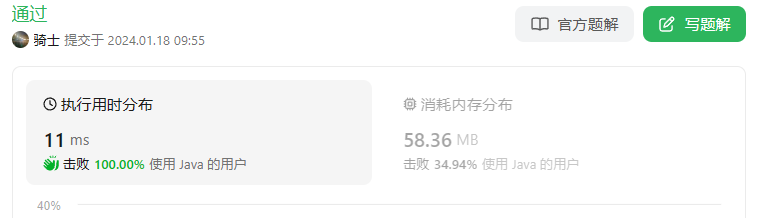
运行结果:
交流
qq群:136156434


)
)









)





![如何实现指定列值排序? ------ MySQL中的field()函数 [让排序更简单]](http://pic.xiahunao.cn/如何实现指定列值排序? ------ MySQL中的field()函数 [让排序更简单])