优质博文:IT-BLOG-CN
一、题目
给定一个整数数组nums和一个整数目标值target,请你在该数组中找出"和"为目标值target的那两个整数,并返回它们的数组下标。
你可以假设每种输入只会对应一个答案。但是,数组中同一个元素在答案里不能重复出现。
你可以按任意顺序返回答案。
示例 1:
输入:nums = [2,7,11,15], target = 9
输出:[0,1]
解释:因为nums[0] + nums[1] == 9,返回[0, 1]。
示例 2:
输入:nums = [3,2,4], target = 6
输出:[1,2]
示例 3:
输入:nums = [3,3], target = 6
输出:[0,1]
2 <= nums.length <= 104
-109 <= nums[i] <= 109
-109 <= target <= 109
只会存在一个有效答案
进阶: 你可以想出一个时间复杂度小于O(n2)的算法吗?
二、代码
哈希表思路:
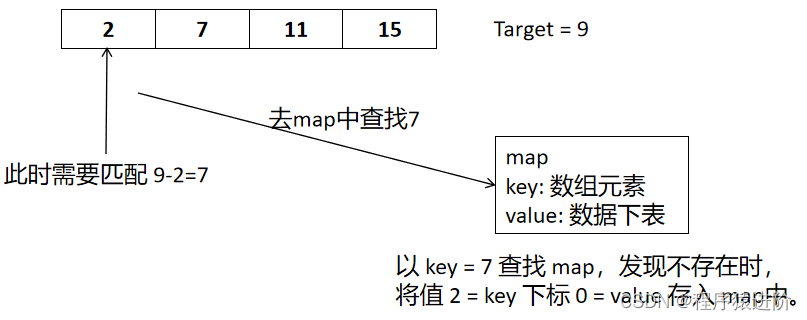
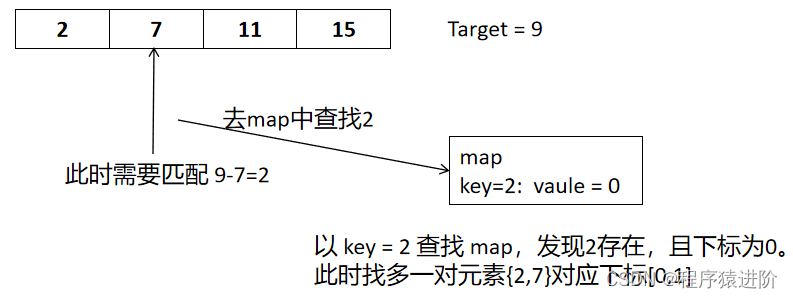
【1】先获取数组中的第一个元素,通过target - num[i] = x,直接过去x的下标,存在直接返回当前索引和查询到的索引,但需要对[3,3]=6等特殊场景进行处理。
【2】们发现这个题目属于hash表下面的,所以使用hash表来实现。可以用key保存数值,用value在保存数值所在的下标。map中的存储结构为{key:数据元素,value:数组元素对应的下表}
在遍历数组的时候,只需要向map去查询是否存在target - num[i] = x中的x,如果存在,就返回value也就是下标和i,如果没有,就把目前遍历的元素放进map中,因为map存放的就是我们访问过的元素。
class Solution {public int[] twoSum(int[] nums, int target) {// 先获取数组中的第一个元素,通过 target - num[i] = x, 直接过去x的下标,存在直接返回,需要对[3,3]相同的做特殊处理。// 我们发现这个题目属于 hash表下面的,所以使用hash表来实现。可以用key保存数值,用value在保存数值所在的下标// map中的存储结构为 {key:数据元素,value:数组元素对应的下表}int[] res = new int[2];Map<Integer,Integer> map = new HashMap();for (int i = 0; i < nums.length; i++) {int x = target - nums[i];if (map.containsKey(x)) {res[0] = map.get(x);res[1] = i;return res;}map.put(nums[i], i);}return res;}
}
时间复杂度: O(N),其中N是数组中的元素数量。对于每一个元素x,我们可以O(1)地寻找target - x。
空间复杂度: O(N),其中N是数组中的元素数量。主要为哈希表的开销。
暴力枚举: 最容易想到的方法是枚举数组中的每一个数x,寻找数组中是否存在target - x。
当我们使用遍历整个数组的方式寻找target - x时,需要注意到每一个位于x之前的元素都已经和x匹配过,因此不需要再进行匹配。而每一个元素不能被使用两次,所以我们只需要在x后面的元素中寻找target - x。
class Solution {public int[] twoSum(int[] nums, int target) {int n = nums.length;for (int i = 0; i < n; ++i) {for (int j = i + 1; j < n; ++j) {if (nums[i] + nums[j] == target) {return new int[]{i, j};}}}return new int[0];}
}
时间复杂度: O(N^2),其中N是数组中的元素数量。最坏情况下数组中任意两个数都要被匹配一次。
空间复杂度: O(1)。
思考:
1、如果nums是有序的,是否还需要哈希表?换句话说,能否做到O(1)额外空间?
2、如果要求寻找三个数,它们的和等于target呢?
含有重复元素的两数之和(字节算法工程师面试题) :给定一个可能包含重复元素的有序数组,以及一个目标值target。计算数组中有多少对两个整数的组合满足和等于target。
示例1: nums=[2,2,2,2], target= 4, ans=6
示例2: nums=[1,1,2,2,2,2,3,3], target=4, ans=10
示例3: nums=[1,1,1,1], target=4, ans=0
其实第一眼看上去倒也不难,就是一个变体的两数之和。所以刚开始的思路就是先统计每一个数出现的次数,然后再按照两数之和的方法去算,只不过算的时候要考虑两个数出现的次数相乘才是所有的组合。
但是面试官说还有更好的,让我往三数之和上想。但是我想偏了,我一直想的是在三数之和中如果当前数和前一个数相等,那么会直接跳过。这里的话应该是可以根据前一个数对答案的贡献度直接推出来当前数的贡献度的。比如[1,1,2,2,2,2,4,4]的测试用例,首先第一次计算出第一个1对结果的贡献度是2之后,指针右移,又遇到一个1,那么可以不用计算,直接加上上一次的答案,同理,第一次遇到2也是,但是由于2 = 4 - 2,所以,第二次遇到2的时候,不能直接加上上一次的答案,应该加上上一次的答案-1。
import bisect
def solve(nums, target):ans = 0pre = 0for i, num in enumerate(nums):if num == target - num:r = bisect.bisect_right(nums, num)ans += (r - i) * (r - i - 1) // 2return ansif i > 0 and nums[i-1] == num:ans += precontinuel, r = bisect.bisect_left(nums, target - num), bisect.bisect_right(nums, target - num)if l < r:ans += r - lpre = r - lreturn ans
面试完又想了一下另一个思路,可以按照三数之和内层循环的思路,用两个指针分别指向首尾,
1、如果这两个数的和小于taregt,右移左指针,
2、如果大于target,左移右指针。
3、如果等于target,分情况讨论
4、如果两个数相等,可以直接计算,然后终止循环。因为数组有序,继续循环下去也没意义。
5、如果两个数不相等,分别计算出左右两个数出现的次数。然后再计算对答案的贡献度。
时间复杂度: 因为每个数最多只会遍历一次,所以是O(n)
空间复杂度: 只需要常数级的额外空间,所以是:O(1)
class Solution:def twoSum(self, nums: List[int], target: int) -> List[int]:ans = 0left, right = 0, len(nums) - 1while left <= right:current_sum = nums[left] + nums[right]if current_sum == target:# 找到一组满足条件的组合if nums[left] == nums[right]:ans += (right - left + 1) * (right - left) // 2break# 统计左右两个数各自出现的次数left_num, right_num = 1, 1left += 1right -= 1while left <= right and nums[left] == nums[left - 1]:left_num += 1left += 1while left <= right and nums[right] == nums[right + 1]:right_num += 1right -= 1ans += left_num * right_numelif current_sum < target:left += 1else:right -= 1return ans












—— 全局变量)




)

