Monorepo uniapp 

构建灵感：刚好要做一个项目，于是想到升级一下之前自己写的一个vue3+ts+pinia+uno的模版框架，其实那个框架也不错；只是感觉还差点东西，我已经用那个小框架写了两三个项目；轻巧实用。为什么选择去基于vben3构建uniapp 的monorepo架子，主要还是热爱，想去探索，去感受一下前沿的一些技术；生命在于折腾。

uni-app Vue3 + TypeScript + Vite + Pinia + Unocss 模板项目

uniapp-ts-unocss-pinia-vue3-demo 项目代码https://gitee.com/ggbhack/uniapp-ts-unocss-pinia-vue3-demo.git用它做过的项目：

【把货】小程序

【赛客定位】小程序

【游记】h5

monorepo-uniapp项目代码仓库https://gitee.com/ggbhack/monorepo-uniapp.git以上两个项目，喜欢研究的朋友也可以拿去自己改造改造；

vben3 参考基础https://vbenjs.github.io/vben3-doc/

项目架构搭建中

---

- [x] vite-config

- [x] ts-config

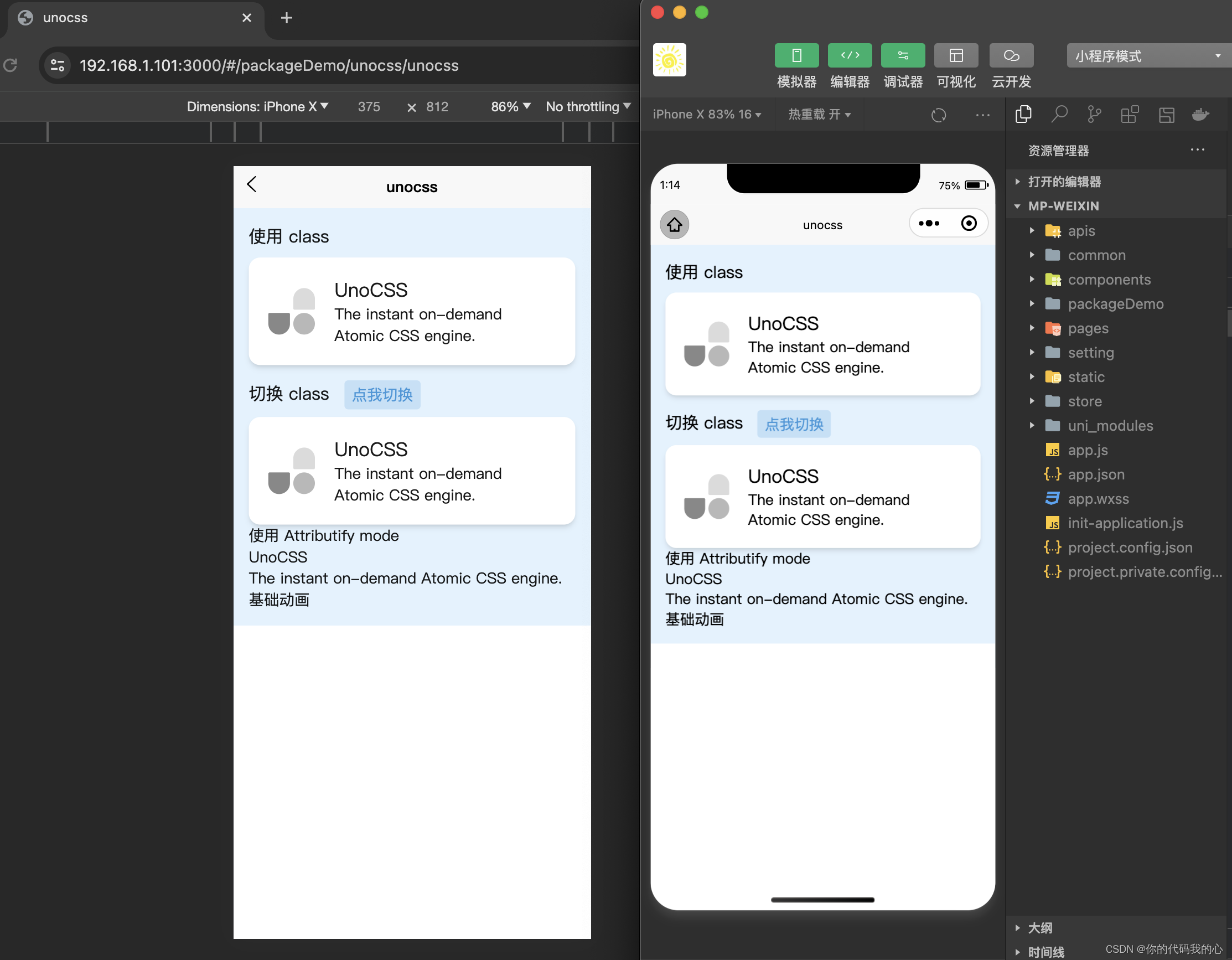
- [x] unocss 样式

- [x] pinia 状态管理

- [x] env 环境变量

- [x] uview-plus ui库

- [x] mescroll-uni 刷新组件

- [x] lint-staged 提交前校验

- [x] pinia 缓存

还有一些其他的就不列出来；

---

以下遇到的问题汇总

为什么 uni-app (vue3) 和 @vueuse/core v10 一起用会报错？参考https://juejin.cn/post/7308899425149042739

function createMockComponent(name) {return {setup() {throw new Error(`[vue-demi] ${name} is not support vue2`)},}}export var TransitionGroup = /*__PURE__*/ createMockComponent('TransitionGroup')

Error: module 'common/side-channel.js' is not defined, require args is 'side-channel'https://ask.dcloud.net.cn/question/177458

qs版本问题，换成6.5.3或其他版本试试

[uniapp 封装axios adapter 运行到小程序报错 Module not found: Error: Package path ./lib/core/settle is not exported from package D:\xxx\xxx\n..https://www.jianshu.com/p/d1d6e0751d97

更换axios的版本为 "axios": "^0.26.1"

多语言打包小程序无效

换一种方式引入

import zh_CN from './lang/zh_CN'import en from './lang/en'// 这里改用另外一种方式// const defaultLocal = await import(`./lang/${locale}.ts`);// const message = defaultLocal.default?.message ?? {};const messages: Record<string, any> = {en,zh_CN}// // const defaultLocal = zh_CN;// const message = defaultLocal ?? {};const message = messages[locale].message ?? {}

改造 getAppConfig

// 打包微信小程序报错 __PRODUCTION__VBEN_ADMIN__ 报错无法读取function getAppConfig(env: Record<string, any>) {// const ENV_NAME = getAppConfigFileName(env)// const ENV = (// env.DEV// ? // Get the global configuration (the configuration will be extracted independently when packaging)// env// : window[ENV_NAME]// ) as GlobEnvConfigconst ENV = env as GlobEnvConfig// console.log(env,env.DEV)const { VITE_GLOB_APP_SHORT_NAME } = ENVif (!/^[a-zA-Z\_]*$/.test(VITE_GLOB_APP_SHORT_NAME)) {console.warn(`VITE_GLOB_APP_SHORT_NAME Variables can only be characters/underscores, please modify in the environment variables and re-running.`,)}return ENV}

unocss 打包小程序 样式报错多一个 \

固定unocss的版本号 - 后续看能不能解决控制台的警告

{"unocss": "^0.51.8","unocss-preset-weapp": "^0.2.1"}

[uniapp 的缓存处理 参考]https://blog.csdn.net/weixin_43191327/article/details/134071863

在构建的过程中我移除了一些不必要的依赖包，当然还留了一些；具体可以看对应的代码；

这是我花了几天时间运行完之后的样子；可能还存在一些其他的问题，后续在慢慢的优化。

还是那句话：

一行动，就创新

一具体，就深刻

一困惑，就上网