【C++进阶】心心念念的红黑树，它来了！

在这里插入图片描述

👦个人主页：@Weraphael
✍🏻作者简介：目前学习C++和算法
✈️专栏：C++航路
🐋 希望大家多多支持，咱一起进步！😁
如果文章对你有帮助的话
欢迎评论💬 点赞👍🏻 收藏 📂 加关注✨

一、红黑树的概念
二、红黑树的规则总结
三、红黑树的定义
四、新增结点颜色的选择
五、插入分析及代码实现
- - 5.1 前言
  - 5.2 uncle存在且为红
  - 5.3 当uncle不存在
  - 5.4 uncle存在且为黑
六、对插入操作总结一波
- - 6.1 uncle存在且为红
  - 6.2 uncle不存在或uncle存在且为黑
  - 6.3 代码实现
七、验证红黑树
八、红黑树与AVL树的比较
九、代码

一、红黑树的概念

红黑树是除AVL-tree之外，另一个被广泛运用的平衡二叉搜索树。
红黑树比AVL-tree还牛逼。这是因为AVL-tree需要严格遵守平衡因子不超过1的规则；而红黑树是 通过颜色（红/黑）的限制，来达到最长路径不超过最短路径的2倍，因此并不是严格的平衡，而是近似平衡。

二、红黑树的规则总结

每个结点不是红色就是黑色。
根节点必须是黑色的。
如果一个节点是红色的，那么它的孩子结点必须是黑色的（说明任何路径不可能存在连续的红色结点）
对于每个结点，从根到空结点NIL，黑色结点的数量相等。
每个空结点NIL都是黑色的。

需要注意的是，在红黑树中，路径是由根结点到空结点。

根据以上规则，一颗红黑树就诞生了

在这里插入图片描述

上图中，红黑树的路径有11条！

三、红黑树的定义

红黑树和AVL-tree都是一个三叉链结构，只是控制平衡的方式不同，红黑树是通过颜色来控制的

#pragma once#include <utility>
#include <iostream>
using namespace std;// 颜色
enum Colour
{RED,BLACK
};template <class K, class V>
struct RBTreeNode 
{pair<K, V> _key;struct RBTreeNode<K, V>* _left;struct RBTreeNode<K, V>* _right;struct RBTreeNode<K, V>* _parent;Colour _col;RBTreeNode(const pair<K, V>& kv):_key(kv),_left(nullptr),_right(nullptr),_parent(nullptr),_col(RED){}
};template <class K, class V>
class RBTree
{typedef struct RBTreeNode<K, V> Node;public:// 默认构造RBTree():_root(nullptr){}private:Node* _root;
};

为什么要定义parent指针，详细讲解请参考AVL章节：点击跳转

四、新增结点颜色的选择

在红黑树中，新增的默认结点颜色可以选择红色，也可以选择黑色。但是，建议选择红色。

接下来分析为什么选择红色。

如果为新增结点默认为红色，可能违反原则3：【如果一个节点是红色的，它的孩子结点必须是黑色的】，那么需要进行适当调整。当然也可能不需要调整。

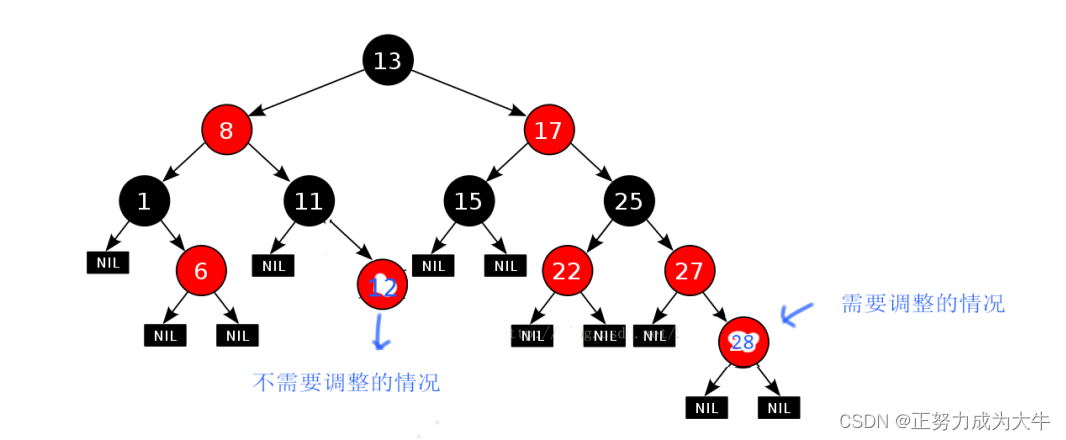
在这里插入图片描述

如果为新增结点默认为黑色，必然违反原则4：【对于每个结点，从根到空结点NIL，黑色结点的数量相等】，并且因为这一条路，影响了其他所有路径，可能需要对现有的红黑树进行更多的旋转和重新着色操作，从而导致更大的改动，增加了调整平衡的复杂度。

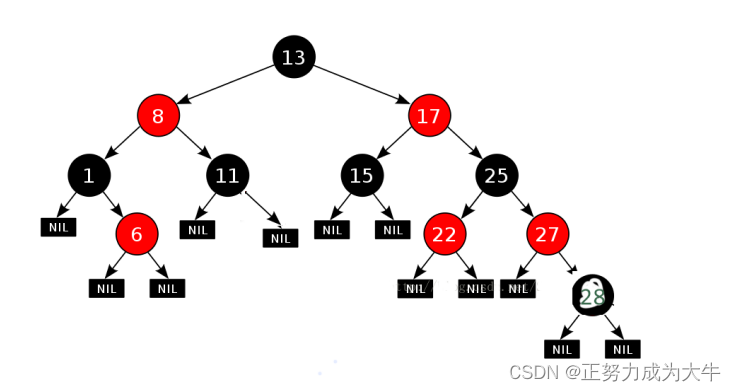
在这里插入图片描述

因此，为了尽可能少地改变树的结构，让新结点默认为红色，插入后，不一定调整，但即使调整，也不至于影响全局。

五、插入分析及代码实现

5.1 前言

RB-tree的平衡条件虽然不同于AVL-tree，但同样运用了单旋转和双旋转来调节平衡。

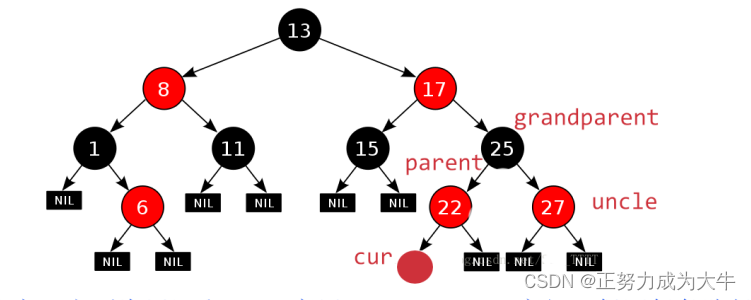
为了方便讨论，可以为某些特殊结点“取别名”。

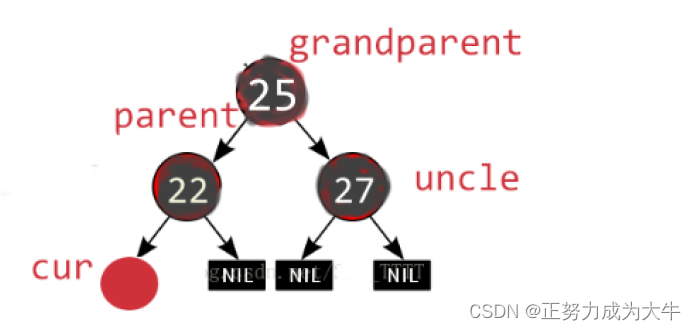
插入的新结点为cur
新结点的父结点为parent
新结点的祖父结点为(父结点的父亲)grandparent
叔叔结点(父结点的兄弟结点)为uncle

通常情况下，我们会 特别关注叔叔结点。具体来说会有以下三种情况：

5.2 uncle存在且为红

当cur插在parent的左边时

解决方法：变色 + 继续向上更新看是否需要调整。

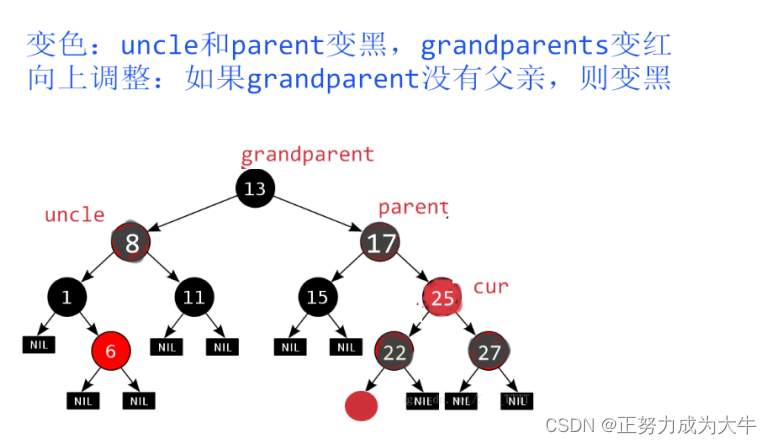
【变色】：结点parent（父亲结点一定要为黑色）和uncle变黑，grandparent变红。变色操作是保证每条路径的黑节点个数相同，并且在grandparent这个子树中，暂时解决了出现连续的红结点的情况。
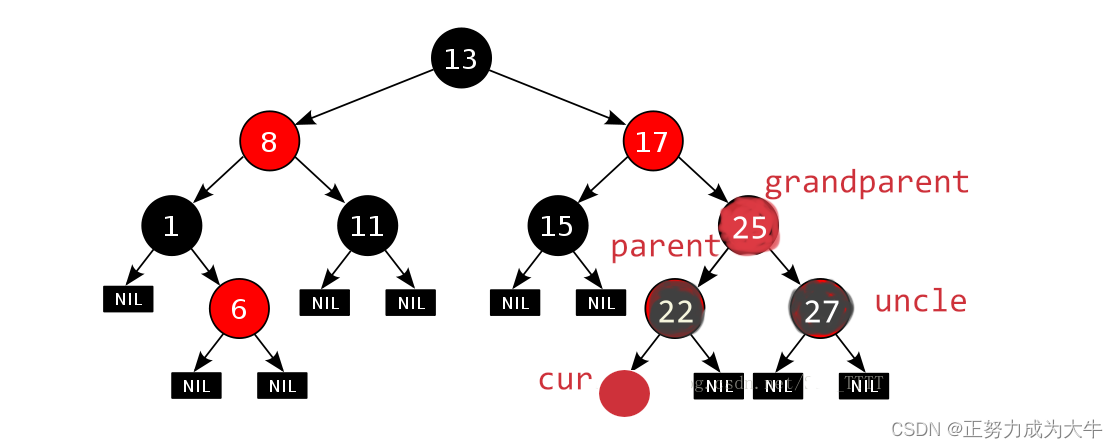
【向上调整】：解决整个树可能出现连续红结点情况（三种）：

① 如果grandparent没有父亲：将祖父grandparent变黑即可。

在这里插入图片描述

② 如果grandparent有父亲，且父亲是黑色的，那么不用调整。

③ 如果grandparent有父亲，且父亲是红色的，就要向上进行调整，因为不能出现连续的红色结点。具体的情况也就只有3种

比如说以下这种：
在这里插入图片描述

此时uncle为红色，并且cur插在parent的右边。虽然插入位置不同，但解决方法还是一样的。

当cur插在parent的右边时

解决方法：变色 + 继续向上更新看是否需要调整。详细细节可以看看上面的解释说明

在这里插入图片描述

5.3 当uncle不存在

当uncle不存在于grandparent的右边时

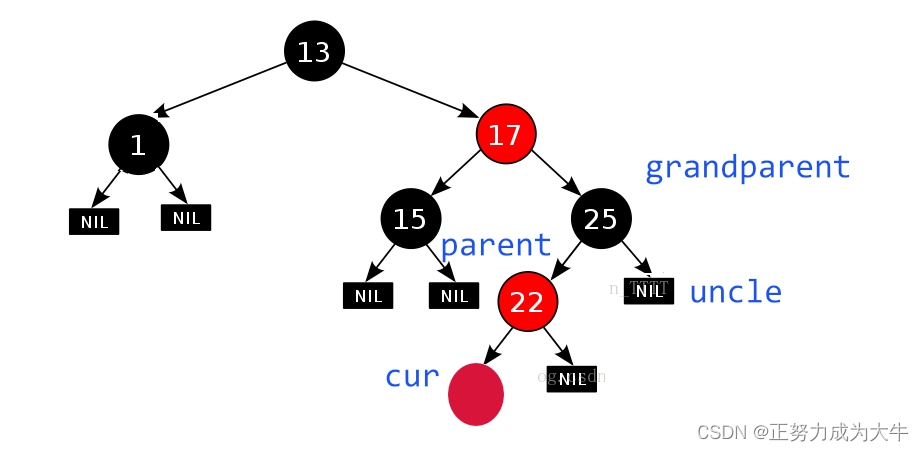
在这里插入图片描述

解决方法：旋转 + 变色。

【旋转】：什么旋转是根据cur插入的位置来定的。如果插入在parent的左边，那么就要以grandparent结点进行右单旋；如果插入在parent的右边，就要进行双旋，先左单旋，最后再右单旋。

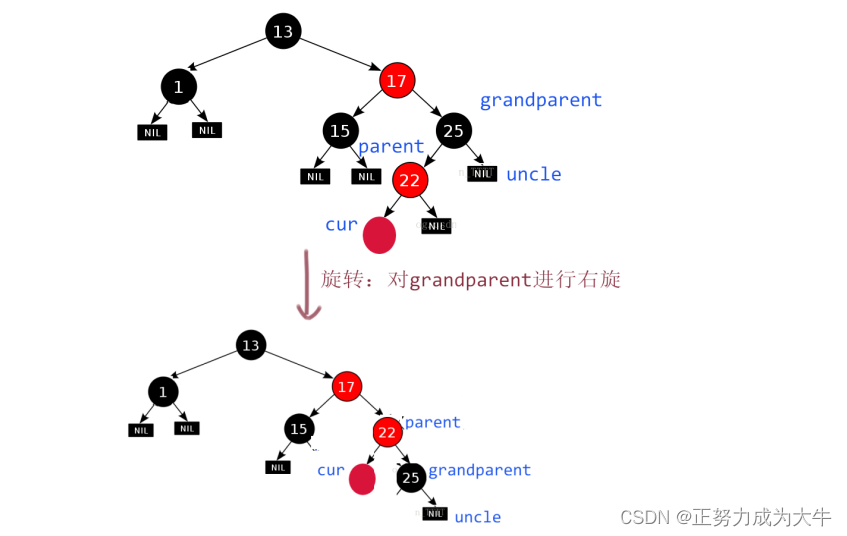
在这里插入图片描述

【变色】：parent变黑，grandparent变红。

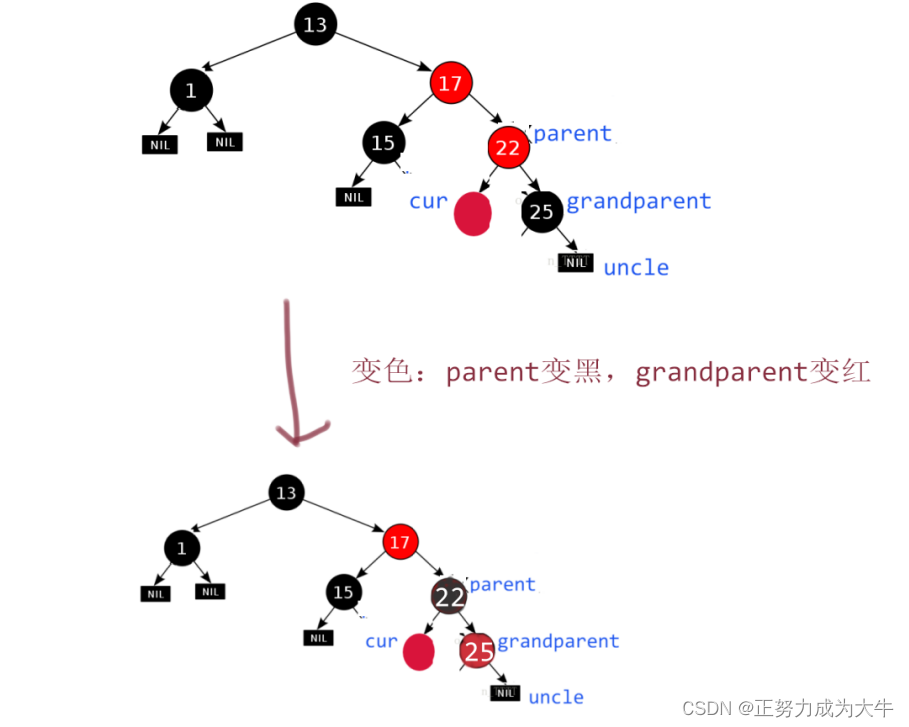
在这里插入图片描述

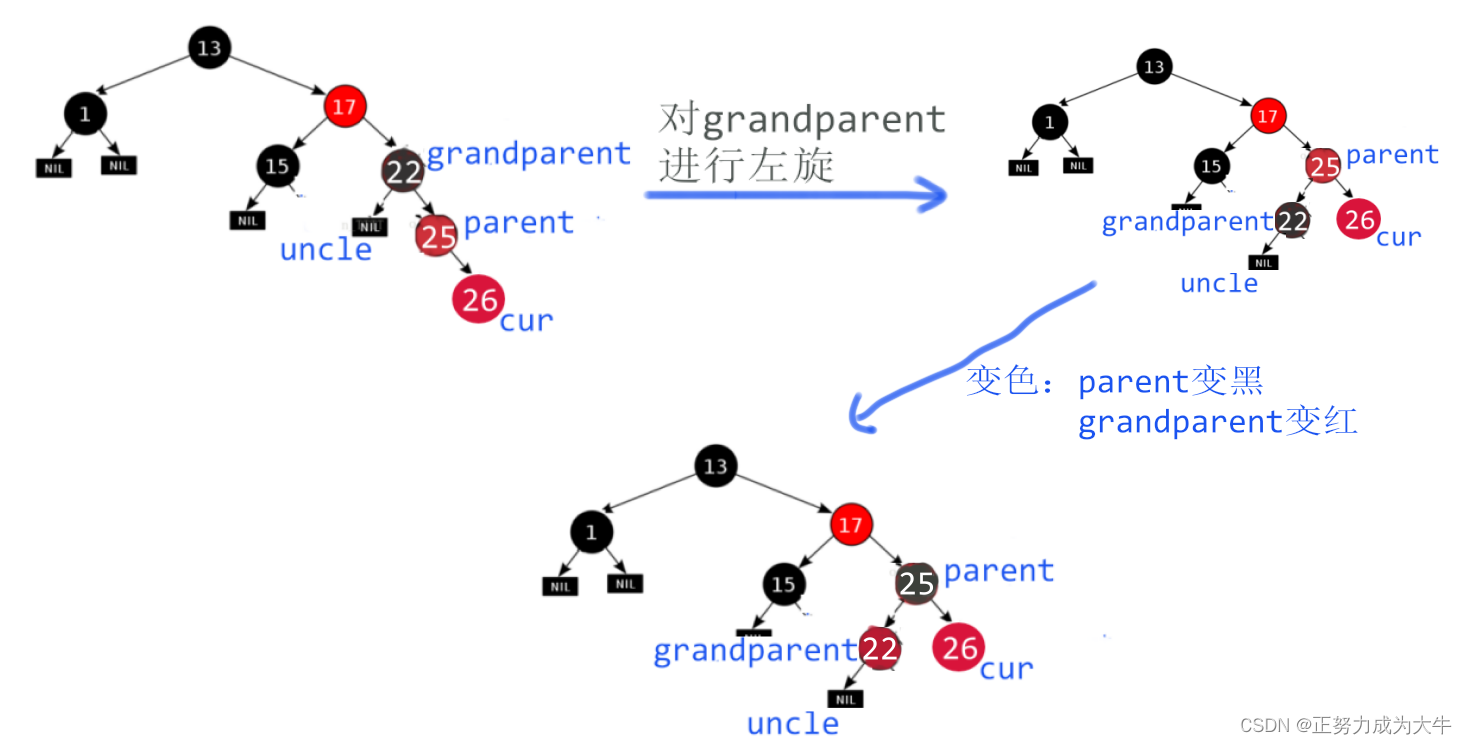
当uncle不存在于grandparent的左边时

解决方法还是一样：旋转 + 变色。这里就不再重点讲解了，大家看看下图来领会吧 ~

在这里插入图片描述

接下来再基于uncle不存在时，看看 【双旋】 是怎么个事：

当uncle不存在于grandparent的左边时

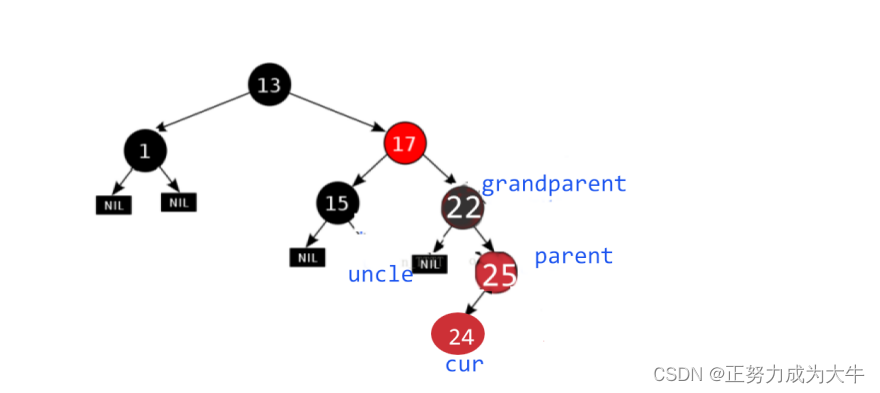
在这里插入图片描述

解决方法同样是变色

【双旋】：我们在上面说过，对于uncle不存在于grandparent的左边这种情况，并且cur插入在parent的左侧，那么就要进行双旋。首先先对parent进行右单旋；再对parent进行左单旋。

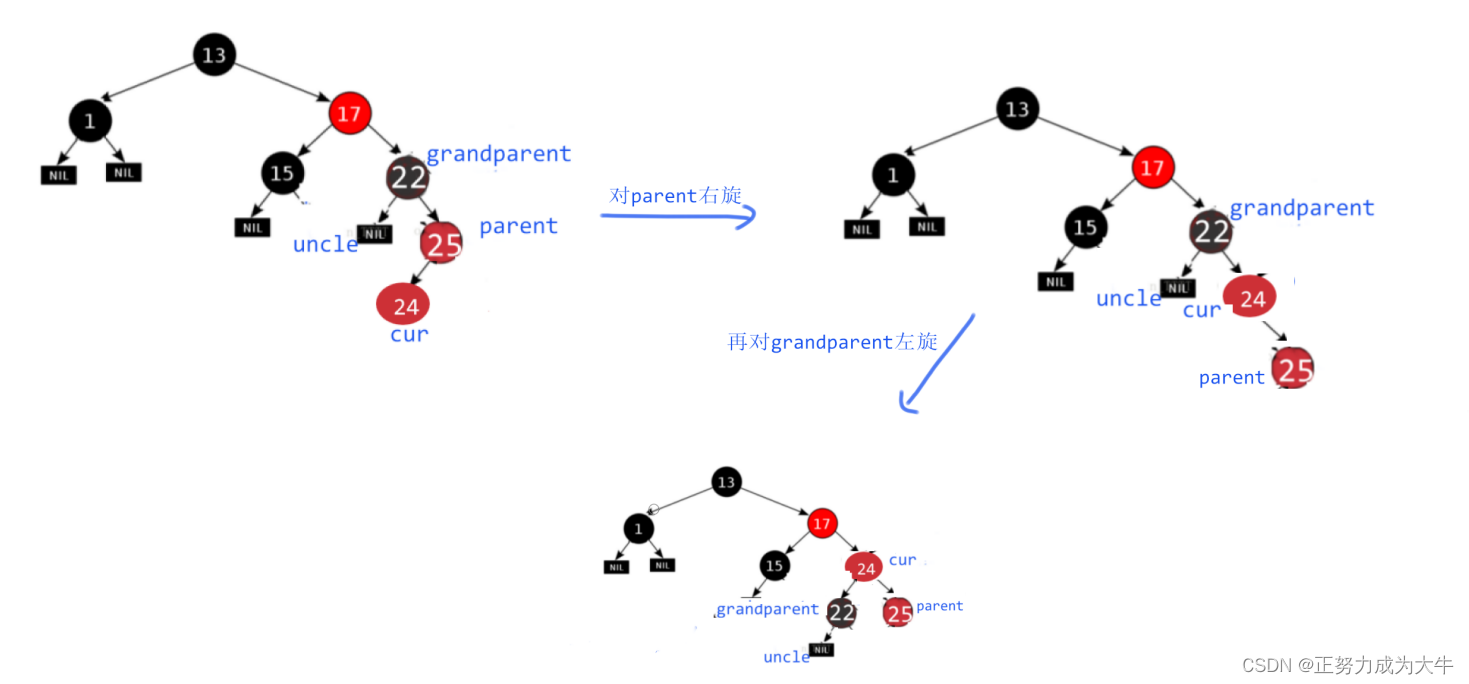
在这里插入图片描述

【变色】：将cur变黑，grandparent变红

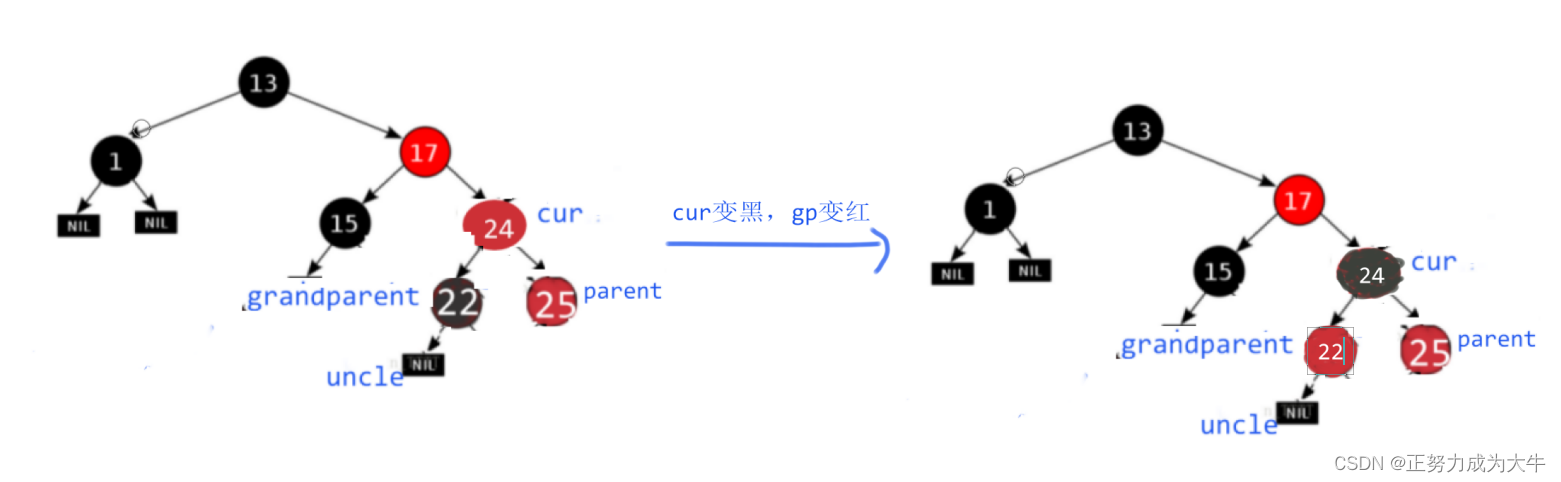
在这里插入图片描述

当然了，对于对于uncle不存在于grandparent的右边这种情况，并且cur插入在parent的右侧。这种调整的解决方法同样是双旋 + 变色。双旋是先对于parent左旋转，再对grandparent右旋，最后再将cur变黑以及grandparent变红。由于演示的样例过多，这里就不再演示了hh

5.4 uncle存在且为黑

来看看一下这种情况
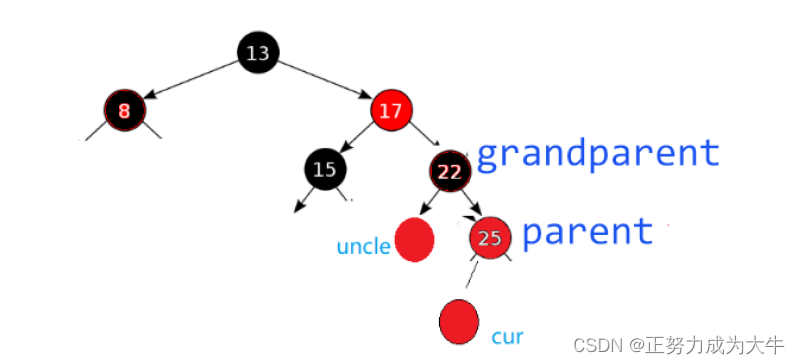
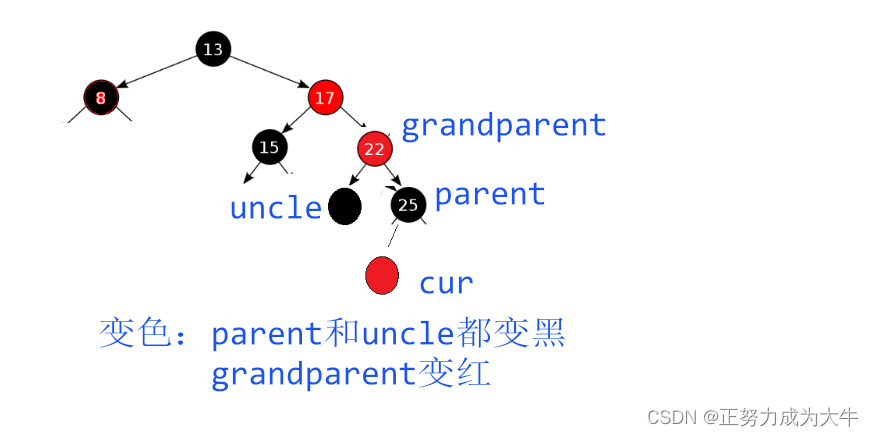
在这里插入图片描述

首先我们需要处理uncle存在且为红的情况，解决方法很简单：变色 + 继续向上更新

在这里插入图片描述

继续向上更新时，就出现了uncle存在且为黑的情况

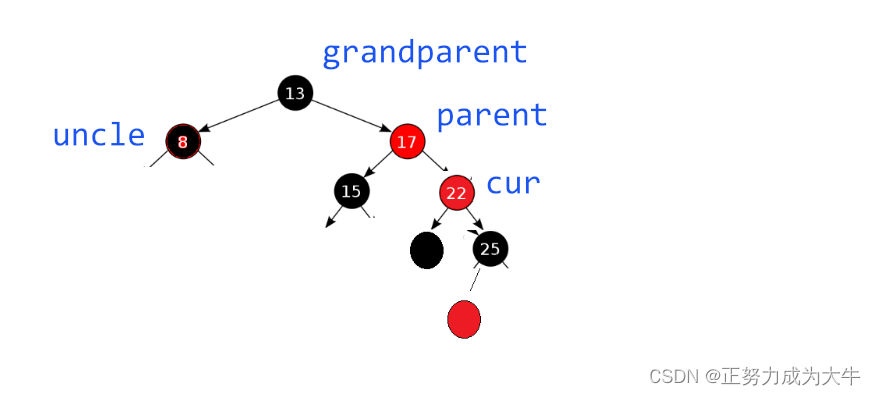
在这里插入图片描述

解决方法：旋转 + 变色（parent变黑、grandparents变红）

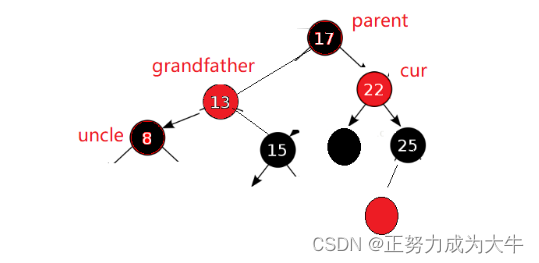
在这里插入图片描述

我们发现：uncle存在且为黑的情况好像和uncle不存在的解决方法是一模一样的，因此我们可以将其归为一类。

六、对插入操作总结一波

6.1 uncle存在且为红

在这里插入图片描述

解决方式：变色 + 向上调整

【变色】：将parent和unlce改为黑，grandparent改为红。

【向上调整】：把grandparent当成cur，继续向上调整。在调整的过程中，如果grandparent是根结点，则直接将其变黑。

6.2 uncle不存在或uncle存在且为黑

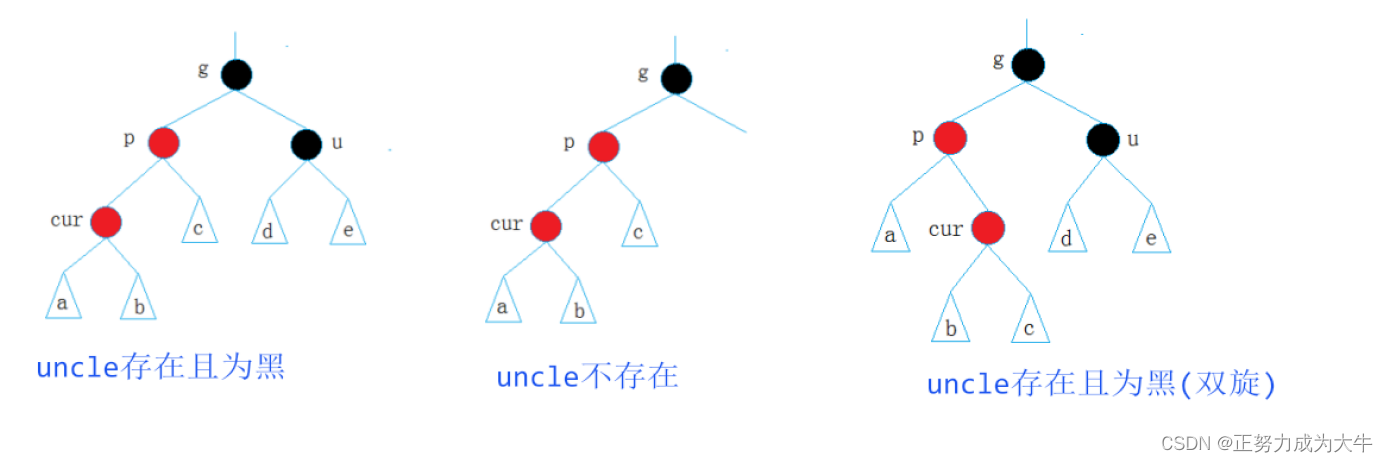
在这里插入图片描述

解决方法：旋转 + 变色

注意：什么旋转是根据cur插入的位置来定的。

【单旋转】 如果cur插入在parent的左边，那么就要以grandparent结点进行右单旋
【变色】 parent变成黑色，grandparent变为红色。

【双旋转】 如果cur插入在parent的右边，就要进行双旋，先左单旋，最后再右单旋。
【变色】 cur变成黑色（旋转后cur变为根了，根一定为黑），grandparent变为红色。

当然了，以上的情况均是以parent作为grandparent的左孩子分析的，还需要考虑parent作为grandparent的右孩子，其本质是不变。我大致为大家总结了一下：

不需要旋转的代码都一样。
旋转部分的代码要注意结点的方向。

6.3 代码实现

bool Insert(const pair<K, V>& key)
{// 如果一开始根结点为空，直接插入即可if (_root == NULL){_root = new Node(key); // new会自动调用自定义类型的构造函数_root->_col = BLACK; // 规则1：根结点_root必须是黑色的return true;}// 如果一开始根结点不为空，就要找到合适的位置插入Node* parent = nullptr;Node* cur = _root;while (cur){if (cur->_key.first < key.first){parent = cur;cur = cur->_right;}else if (cur->_key.first > key.first){parent = cur;cur = cur->_left;}else // 出现数据冗余，插入失败{return false;}}// 当cur走到空，说明已经找到了合适的位置cur = new Node(key);cur->_col = RED; // 插入的新结点必须是红色的if (parent->_key.first < key.first){parent->_right = cur;}else{parent->_left = cur;}cur->_parent = parent;// 控制平衡：通过颜色(红/黑)的限制，来达到最长路径不超过最短路径的2倍while (parent && parent->_col == RED) // 向上调整的条件{Node* grandparent = parent->_parent; // 找祖父// 如果父亲在祖父的左边if (parent == grandparent->_left){// 那么uncle一定在祖父的右边Node* uncle = grandparent->_right;// 情况1：如果uncle存在且为红if (uncle && uncle->_col == RED){// 解决方法：父亲和叔叔的颜色变黑，祖父变红 + 向上处理parent->_col = uncle->_col = BLACK;grandparent->_col = RED;// 向上处理cur = grandparent;parent = cur->_parent;}// 情况2：叔叔不存在或叔叔存在且为黑// 解决方法：旋转 + 变色else{// 1. 插入在parent的左边：单旋 + 变色if (cur == parent->_left){//     g//   p// c// 右单旋转RotateRight(grandparent);// 变色parent->_col = BLACK;grandparent->_col = RED;}// 2. 插入在parent的右边：双旋 + 变色else{//     g//   p//     cRotateLeft(parent);RotateRight(grandparent);cur->_col = BLACK;grandparent->_col = RED;}// 旋转完之后红黑树一定平衡，不需要向上调整// 因为旋转后，树/子树的根一定是黑色break;}}else // parent == grandparent->_right{// parent在grandparent的右，那么uncle一定在grandparent的左Node* uncle = grandparent->_left;// 情况1：如果uncle存在且为红// 解决方法：父亲和叔叔的颜色变黑，祖父变红 + 向上处理if (uncle && uncle->_col == RED){// 变色parent->_col = uncle->_col = BLACK;grandparent->_col = RED;// 向上处理cur = grandparent;parent = cur->_parent;}// 情况2：uncle不存在且uncle为黑else{if (cur == parent->_right){//  g//     p//        cRotateLeft(grandparent);grandparent->_col = RED;parent->_col = BLACK;}else{//  g//     p//  cRotateRight(parent);RotateLeft(grandparent);cur->_col = BLACK;grandparent->_col = RED;}break;}}}// 当循环退出来到此处，有两种情况// 第一种是break出来的，那么红黑树是百分之百已经调整好的// 还有一种是向上调整的过程中父亲为空，那么此时根结点可能为空// 因此我们可以直接进行暴力处理将根结点的颜色变为黑。因为根为黑是必定的！_root->_col = BLACK; return true;
}

至于旋转代码大家可以参考AVL树的博客：点击跳转。
或者参考我的代码仓库：点击跳转

七、验证红黑树

注意：不能使用最长路径（高度）不能超过最短路径的2倍来验证，因为你写的程序有可能会破坏红黑树的规则，比如说你写的红黑树可能会出现连续的红色结点，可能会出现最长路径不会超过最短路径的2倍。我们这里使用红黑树的规则来进行检查。

// backnumber - 用于统计黑色结点的数量
// benchmark - 基准值。此变量是为了求出一条路径的黑色结点个数作为基准值
bool CheckColour(Node* root, int blacknums, int benchmark)
{if (root == nullptr){// 前序遍历走到空就拿backnumber与基准值benchmark比较即可if (blacknums != benchmark){return false;}return true;}// 2. 每条路径的黑色结点数量相等if (root->_col == BLACK) // 遇到黑结点backnumber自增1{++blacknums;}// 2. 不可能出现连续的红结点// 检查当前结点的颜色和其父亲结点的颜色即可if (root->_col == RED && root->_parent && root->_parent->_col == RED){cout << root->_key.first << "连续红色结点" << endl;return false;}// 递归检查左子树和右子树return CheckColour(root->_left, blacknums, benchmark)&& CheckColour(root->_right, blacknums, benchmark);
}bool _IsBalance(Node* root)
{// 根结点为空也算红黑树if (root == nullptr){return true;}// 1. 每个结点不是红色就是黑色。(这个不需要验证)// 2. 根节点必须是黑色的。if (root->_col != BLACK){return false;}int benchmark = 0;	Node* cur = _root;while (cur){if (cur->_col == BLACK){++benchmark;}cur = cur->_left;}// 3. 颜色的检查return CheckColour(root, 0, benchmark);
}

八、红黑树与AVL树的比较

红黑树和AVL树都是自平衡的二叉搜索树，它们在维护树的平衡性方面有些不同，因此在不同的应用场景下会有不同的性能表现。

平衡性：
- AVL树：AVL树通过保持任意节点的左右子树高度之差不超过1来维护平衡。（严格平衡）
- 红黑树：红黑树通过保持以五个性质来维护平衡。（近似平衡）
插入和删除操作：
- AVL树：AVL树在进行插入和删除操作时，也会通过旋转来调整树的结构并保持平衡。但相比红黑树，AVL树对平衡的要求更加严格，可能需要进行更多的旋转操作。这使得插入和删除操作的时间复杂度略高于红黑树，为O(log n)。
- 红黑树：红黑树在进行插入和删除操作时，只需通过旋转和颜色变换来调整树的结构并保持平衡。这些操作的时间复杂度为O(log n)，其中n是树的节点数量。
查询操作：
- 红黑树和AVL树在查询操作上具有相同的时间复杂度，都为O(log n)。这是因为它们都是二叉搜索树，具有相似的查找性能。
存储空间：
- 红黑树：红黑树通过颜色标记来维护平衡，需要额外存储每个节点的颜色信息，因此在空间上稍微占用更多的内存。
- AVL树：AVL树不需要额外的信息来维护平衡，因此在空间上相对较小。

综上所述：红黑树和AVL树都是高效的平衡二叉树，增删改查的时间复杂度都是O( $log_2 N$ )，红黑树不追求绝对平衡，其只需保证最长路径不超过最短路径的2倍，相对而言，降低了插入和旋转的次数，所以在经常进行增删的结构中性能比AVL树更优，而且红黑树实现比较简单，所以实际运用中红黑树更多。