C++力扣题目501--二叉搜索树中的众数

给你一个含重复值的二叉搜索树（BST）的根节点 root ，找出并返回 BST 中的所有众数（即，出现频率最高的元素）。

如果树中有不止一个众数，可以按 任意顺序 返回。

假定 BST 满足如下定义：

结点左子树中所含节点的值 小于等于 当前节点的值
结点右子树中所含节点的值 大于等于 当前节点的值
左子树和右子树都是二叉搜索树

示例 1：

输入：root = [1,null,2,2]
输出：[2]

示例 2：

输入：root = [0]
输出：[0]
提示：

树中节点的数目在范围 [1, 104] 内
-105 <= Node.val <= 105

思路

这道题目呢，递归法我从两个维度来讲。

首先如果不是二叉搜索树的话，应该怎么解题，是二叉搜索树，又应该如何解题，两种方式做一个比较，可以加深大家对二叉树的理解。

#递归法

#如果不是二叉搜索树

如果不是二叉搜索树，最直观的方法一定是把这个树都遍历了，用map统计频率，把频率排个序，最后取前面高频的元素的集合。

具体步骤如下：

这个树都遍历了，用map统计频率

至于用前中后序哪种遍历也不重要，因为就是要全遍历一遍，怎么个遍历法都行，层序遍历都没毛病！

这里采用前序遍历，代码如下：

// map<int, int> key:元素，value:出现频率
void searchBST(TreeNode* cur, unordered_map<int, int>& map) { // 前序遍历if (cur == NULL) return ;map[cur->val]++; // 统计元素频率searchBST(cur->left, map);searchBST(cur->right, map);return ;
}

把统计的出来的出现频率（即map中的value）排个序

有的同学可能可以想直接对map中的value排序，还真做不到，C++中如果使用std::map或者std::multimap可以对key排序，但不能对value排序。

所以要把map转化数组即vector，再进行排序，当然vector里面放的也是pair<int, int>类型的数据，第一个int为元素，第二个int为出现频率。

代码如下：

bool static cmp (const pair<int, int>& a, const pair<int, int>& b) {return a.second > b.second; // 按照频率从大到小排序
}vector<pair<int, int>> vec(map.begin(), map.end());
sort(vec.begin(), vec.end(), cmp); // 给频率排个序

取前面高频的元素

此时数组vector中已经是存放着按照频率排好序的pair，那么把前面高频的元素取出来就可以了。

代码如下：

result.push_back(vec[0].first);
for (int i = 1; i < vec.size(); i++) {// 取最高的放到result数组中if (vec[i].second == vec[0].second) result.push_back(vec[i].first);else break;
}
return result;

整体C++代码如下：

class Solution {
private:void searchBST(TreeNode* cur, unordered_map<int, int>& map) { // 前序遍历if (cur == NULL) return ;map[cur->val]++; // 统计元素频率searchBST(cur->left, map);searchBST(cur->right, map);return ;
}
bool static cmp (const pair<int, int>& a, const pair<int, int>& b) {return a.second > b.second;
}
public:vector<int> findMode(TreeNode* root) {unordered_map<int, int> map; // key:元素，value:出现频率vector<int> result;if (root == NULL) return result;searchBST(root, map);vector<pair<int, int>> vec(map.begin(), map.end());sort(vec.begin(), vec.end(), cmp); // 给频率排个序result.push_back(vec[0].first);for (int i = 1; i < vec.size(); i++) {// 取最高的放到result数组中if (vec[i].second == vec[0].second) result.push_back(vec[i].first);else break;}return result;}
};

所以如果本题没有说是二叉搜索树的话，那么就按照上面的思路写！

#是二叉搜索树

既然是搜索树，它中序遍历就是有序的。

如图：

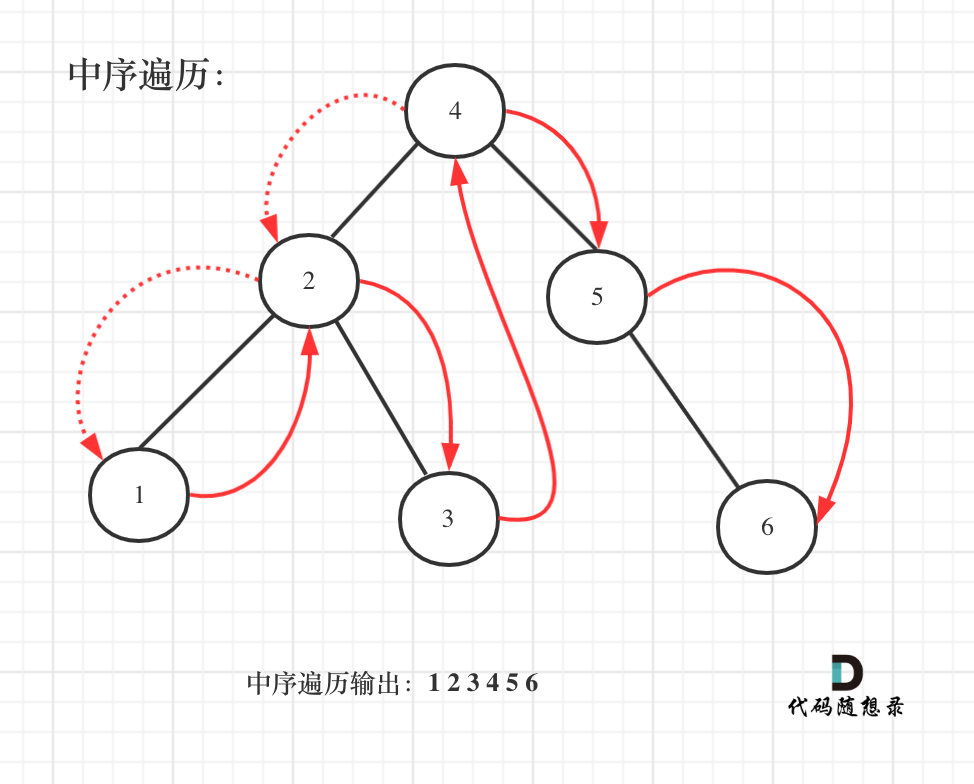
501.二叉搜索树中的众数1

中序遍历代码如下：

void searchBST(TreeNode* cur) {if (cur == NULL) return ;searchBST(cur->left);       // 左（处理节点）                // 中searchBST(cur->right);      // 右return ;
}

遍历有序数组的元素出现频率，从头遍历，那么一定是相邻两个元素作比较，然后就把出现频率最高的元素输出就可以了。

关键是在有序数组上的话，好搞，在树上怎么搞呢？

这就考察对树的操作了。

在二叉树：搜索树的最小绝对差 (opens new window)中我们就使用了pre指针和cur指针的技巧，这次又用上了。

弄一个指针指向前一个节点，这样每次cur（当前节点）才能和pre（前一个节点）作比较。

而且初始化的时候pre = NULL，这样当pre为NULL时候，我们就知道这是比较的第一个元素。

代码如下：

if (pre == NULL) { // 第一个节点count = 1; // 频率为1
} else if (pre->val == cur->val) { // 与前一个节点数值相同count++;
} else { // 与前一个节点数值不同count = 1;
}
pre = cur; // 更新上一个节点

此时又有问题了，因为要求最大频率的元素集合（注意是集合，不是一个元素，可以有多个众数），如果是数组上大家一般怎么办？

应该是先遍历一遍数组，找出最大频率（maxCount），然后再重新遍历一遍数组把出现频率为maxCount的元素放进集合。（因为众数有多个）

这种方式遍历了两遍数组。

那么我们遍历两遍二叉搜索树，把众数集合算出来也是可以的。

但这里其实只需要遍历一次就可以找到所有的众数。

那么如何只遍历一遍呢？

如果频率count 等于 maxCount（最大频率），当然要把这个元素加入到结果集中（以下代码为result数组），代码如下：

if (count == maxCount) { // 如果和最大值相同，放进result中result.push_back(cur->val);
}

是不是感觉这里有问题，result怎么能轻易就把元素放进去了呢，万一，这个maxCount此时还不是真正最大频率呢。

所以下面要做如下操作：

频率count 大于 maxCount的时候，不仅要更新maxCount，而且要清空结果集（以下代码为result数组），因为结果集之前的元素都失效了。

if (count > maxCount) { // 如果计数大于最大值maxCount = count;   // 更新最大频率result.clear();     // 很关键的一步，不要忘记清空result，之前result里的元素都失效了result.push_back(cur->val);
}

关键代码都讲完了，完整代码如下：（只需要遍历一遍二叉搜索树，就求出了众数的集合）

class Solution {
private:int maxCount = 0; // 最大频率int count = 0; // 统计频率TreeNode* pre = NULL;vector<int> result;void searchBST(TreeNode* cur) {if (cur == NULL) return ;searchBST(cur->left);       // 左// 中if (pre == NULL) { // 第一个节点count = 1;} else if (pre->val == cur->val) { // 与前一个节点数值相同count++;} else { // 与前一个节点数值不同count = 1;}pre = cur; // 更新上一个节点if (count == maxCount) { // 如果和最大值相同，放进result中result.push_back(cur->val);}if (count > maxCount) { // 如果计数大于最大值频率maxCount = count;   // 更新最大频率result.clear();     // 很关键的一步，不要忘记清空result，之前result里的元素都失效了result.push_back(cur->val);}searchBST(cur->right);      // 右return ;}public:vector<int> findMode(TreeNode* root) {count = 0;maxCount = 0;pre = NULL; // 记录前一个节点result.clear();searchBST(root);return result;}
};

#迭代法

只要把中序遍历转成迭代，中间节点的处理逻辑完全一样。

二叉树前中后序转迭代，传送门：

二叉树：前中后序迭代法(opens new window)
二叉树：前中后序统一风格的迭代方式(opens new window)

下面我给出其中的一种中序遍历的迭代法，其中间处理逻辑一点都没有变（我从递归法直接粘过来的代码，连注释都没改）

代码如下：

class Solution {
public:vector<int> findMode(TreeNode* root) {stack<TreeNode*> st;TreeNode* cur = root;TreeNode* pre = NULL;int maxCount = 0; // 最大频率int count = 0; // 统计频率vector<int> result;while (cur != NULL || !st.empty()) {if (cur != NULL) { // 指针来访问节点，访问到最底层st.push(cur); // 将访问的节点放进栈cur = cur->left;                // 左} else {cur = st.top();st.pop();                       // 中if (pre == NULL) { // 第一个节点count = 1;} else if (pre->val == cur->val) { // 与前一个节点数值相同count++;} else { // 与前一个节点数值不同count = 1;}if (count == maxCount) { // 如果和最大值相同，放进result中result.push_back(cur->val);}if (count > maxCount) { // 如果计数大于最大值频率maxCount = count;   // 更新最大频率result.clear();     // 很关键的一步，不要忘记清空result，之前result里的元素都失效了result.push_back(cur->val);}pre = cur;cur = cur->right;               // 右}}return result;}
};