
✅作者简介:人工智能专业本科在读,喜欢计算机与编程,写博客记录自己的学习历程。
🍎个人主页:小嗷犬的个人主页
🍊个人网站:小嗷犬的技术小站
🥭个人信条:为天地立心,为生民立命,为往圣继绝学,为万世开太平。
本文目录
- Transformer
- 位置编码
- 什么是位置编码以及为什么需要位置编码
- Transformer 中的位置编码
- 直观理解
- 位置编码如何结合到词向量中
- 相对位置
- 其他问题
- 为什么位置编码与词向量结合是使用相加而不是连接
- 位置编码信息如何传递到模型深层
- 为什么要同时使用正弦和余弦函数
Transformer
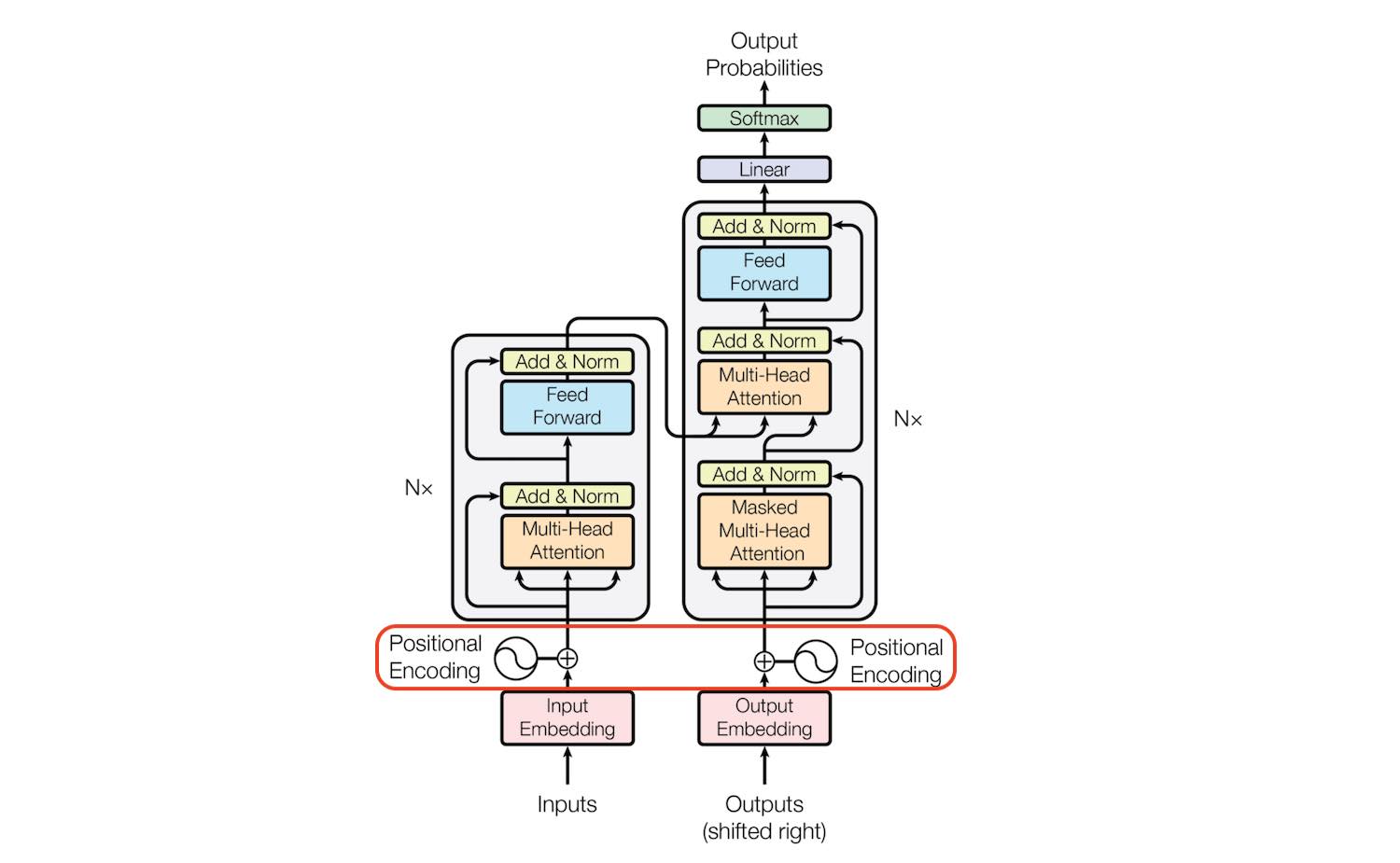
Attention Is All You Need 是 Google 于 2017 年发表的论文,这篇论文提出了一种新的神经网络架构: Transformer,它完全摒弃了传统的 CNN 和 RNN 结构,基于 Attention 机制来实现 Seq2Seq 的建模。
Transformer 的出现是人工智能领域的重大突破,它不仅在机器翻译任务上取得了 SOTA 的效果,而且在其他 NLP 任务上也有着非常好的表现,后续更是被广泛应用于 CV 领域。
位置编码
本文主要介绍 Transformer 中的位置编码,它是 Transformer 中非常重要的一部分。
什么是位置编码以及为什么需要位置编码
词的位置和顺序是任何语言的重要组成部分。它们决定着语法,因此也决定了句子的实际语义。
卷积神经网络(CNN)使用卷积核来捕获单词之间的相对位置信息,但其仅能捕获固定大小的局部上下文信息。
循环神经网络(RNN)在处理序列信息上会有更好的效果,其依靠循环结构,将序列信息逐步传递,这其中就引入了单词的位置和顺序信息。但随着序列长度的增加,RNN 会慢慢忘记早前的信息,这就导致了长期依赖问题。除此之外,循环结构也使得 RNN 无法并行计算,这使得 RNN 的训练速度十分缓慢。
Transformer 放弃了循环结构,而采用了自注意力机制,这使得 Transformer 可以并行计算,从而大大提高了训练速度。同时,自注意力机制也使得 Transformer 可以捕获任意距离的依赖关系,从而解决了长期依赖问题。
但由于 Transformer 不包含任何循环结构,各个单词在 Transformer 中都同时经过 Decoder-Encoder 的变换,这就导致了 Transformer 无法捕获单词的位置信息。
为了解决这个问题,我们需要在输入的单词向量中加入某种信息,以区分每个单词的位置。这一信息被称为位置编码。
一个简单的想法是:我们可以将单词的位置信息映射到 [ 0 , 1 ] [0,1] [0,1] 的范围上,第一个单词的位置信息为 0 0 0,最后一个单词的位置信息为 1 1 1,中间的单词按照固定间隔均匀分配。但这显然会带来一个问题,即在不同长度的句子中,单词位置信息的间隔不统一。
另一个容易想到的做法是:我们可以线性地为单词分配位置编号,第一个单词为 1 1 1,第二个单词为 2 2 2,以此类推。显然,这样可能会导致位置编码在数值上很大,并且模型可能会在后续遇到更长的句子,这其中包含了模型在训练中从未遇见过的位置编号,这可能会影响模型的泛化能力。
因此,一个好的位置编码方式通常需要满足以下条件:
- 它应当为每个时间步(单词在句子中的位置)输出唯一的编码
- 在不同长度的句子中,任何两个时间步之间的距离都应保持一致
- 这个方法应当能够推广到任意长的句子,即位置编码的数值应当是有界的
- 位置编码应当是确定的,即对于相同长度的输入,应当输出相同的位置编码
Transformer 中的位置编码
Transformer 中的位置编码方式满足上述所有条件,是一种简单而有效的位置编码方式。它没有为每个时间步输出单一的数字,而是为每个时间步输出一个 d 维向量,这个向量的维度与 Transformer 的词向量维度相同,这个向量被加到输入的单词向量中,从而为单词向量添加了位置信息。
设 t t t 为单词在句子中的位置, p t ⃗ ∈ R d \vec{p_t} \in \mathbb{R}^d pt∈Rd 为其对应的位置编码, d d d 为位置编码的维度, d ≡ 0 ( m o d 2 ) d \equiv 0 (\mod 2) d≡0(mod2),则函数 f : N → R d f : \mathbb{N} \rightarrow \mathbb{R}^d f:N→Rd 即为位置编码函数,其定义如下:
p t ⃗ ( i ) = f ( t ) ( i ) : = { sin ( ω k . t ) , if i = 2 k cos ( ω k . t ) , if i = 2 k + 1 \begin{align*} \vec{p_t}^{(i)} = f(t)^{(i)} & := \begin{cases} \sin({\omega_k} . t), & \text{if}\ i = 2k \\ \cos({\omega_k} . t), & \text{if}\ i = 2k + 1 \end{cases} \end{align*} pt(i)=f(t)(i):={sin(ωk.t),cos(ωk.t),if i=2kif i=2k+1
其中
ω k = 1 1000 0 2 k / d \omega_k = \frac{1}{10000^{2k / d}} ωk=100002k/d1
从定义中我们可以看出三角函数的频率 ω k \omega_k ωk 沿着向量维度不断减小,因此它的波长形成了一个 2 π 2 \pi 2π 到 10000 ⋅ 2 π 10000 \cdot 2 \pi 10000⋅2π 的等比数列。
对于第 t t t 个单词的位置编码 p t ⃗ \vec{p_t} pt,可以看成由不同频率的正弦余弦对组成的向量( d d d 为偶数):
p t ⃗ = [ sin ( ω 1 . t ) cos ( ω 1 . t ) sin ( ω 2 . t ) cos ( ω 2 . t ) ⋮ sin ( ω d / 2 . t ) cos ( ω d / 2 . t ) ] d × 1 \vec{p_t} = \begin{bmatrix} \sin({\omega_1}.t)\\ \cos({\omega_1}.t)\\ \\ \sin({\omega_2}.t)\\ \cos({\omega_2}.t)\\ \\ \vdots\\ \\ \sin({\omega_{d/2}}.t)\\ \cos({\omega_{d/2}}.t) \end{bmatrix}_{d \times 1} pt= sin(ω1.t)cos(ω1.t)sin(ω2.t)cos(ω2.t)⋮sin(ωd/2.t)cos(ωd/2.t) d×1
直观理解
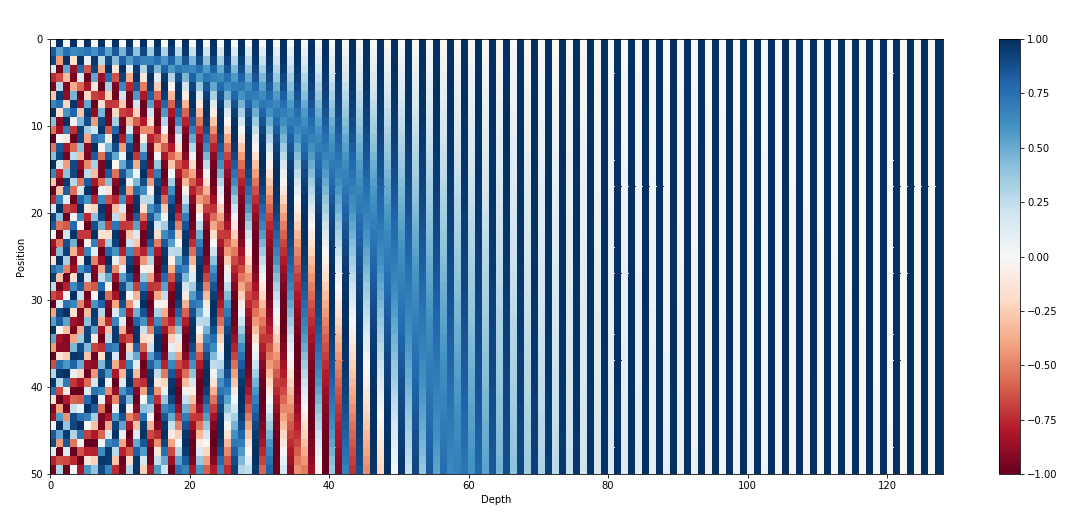
你可能会想知道为什么要用不同频率的正弦余弦对的组合来编码位置信息?
其实这是一个很简单的想法,考虑用二进制编码来表示一个数字的情况:
0 : 0 0 0 0 8 : 1 0 0 0 1 : 0 0 0 1 9 : 1 0 0 1 2 : 0 0 1 0 10 : 1 0 1 0 3 : 0 0 1 1 11 : 1 0 1 1 4 : 0 1 0 0 12 : 1 1 0 0 5 : 0 1 0 1 13 : 1 1 0 1 6 : 0 1 1 0 14 : 1 1 1 0 7 : 0 1 1 1 15 : 1 1 1 1 \begin{align*} 0: \ \ \ \ \color{orange}{\texttt{0}} \ \ \color{green}{\texttt{0}} \ \ \color{blue}{\texttt{0}} \ \ \color{red}{\texttt{0}} & & 8: \ \ \ \ \color{orange}{\texttt{1}} \ \ \color{green}{\texttt{0}} \ \ \color{blue}{\texttt{0}} \ \ \color{red}{\texttt{0}} \\ 1: \ \ \ \ \color{orange}{\texttt{0}} \ \ \color{green}{\texttt{0}} \ \ \color{blue}{\texttt{0}} \ \ \color{red}{\texttt{1}} & & 9: \ \ \ \ \color{orange}{\texttt{1}} \ \ \color{green}{\texttt{0}} \ \ \color{blue}{\texttt{0}} \ \ \color{red}{\texttt{1}} \\ 2: \ \ \ \ \color{orange}{\texttt{0}} \ \ \color{green}{\texttt{0}} \ \ \color{blue}{\texttt{1}} \ \ \color{red}{\texttt{0}} & & 10: \ \ \ \ \color{orange}{\texttt{1}} \ \ \color{green}{\texttt{0}} \ \ \color{blue}{\texttt{1}} \ \ \color{red}{\texttt{0}} \\ 3: \ \ \ \ \color{orange}{\texttt{0}} \ \ \color{green}{\texttt{0}} \ \ \color{blue}{\texttt{1}} \ \ \color{red}{\texttt{1}} & & 11: \ \ \ \ \color{orange}{\texttt{1}} \ \ \color{green}{\texttt{0}} \ \ \color{blue}{\texttt{1}} \ \ \color{red}{\texttt{1}} \\ 4: \ \ \ \ \color{orange}{\texttt{0}} \ \ \color{green}{\texttt{1}} \ \ \color{blue}{\texttt{0}} \ \ \color{red}{\texttt{0}} & & 12: \ \ \ \ \color{orange}{\texttt{1}} \ \ \color{green}{\texttt{1}} \ \ \color{blue}{\texttt{0}} \ \ \color{red}{\texttt{0}} \\ 5: \ \ \ \ \color{orange}{\texttt{0}} \ \ \color{green}{\texttt{1}} \ \ \color{blue}{\texttt{0}} \ \ \color{red}{\texttt{1}} & & 13: \ \ \ \ \color{orange}{\texttt{1}} \ \ \color{green}{\texttt{1}} \ \ \color{blue}{\texttt{0}} \ \ \color{red}{\texttt{1}} \\ 6: \ \ \ \ \color{orange}{\texttt{0}} \ \ \color{green}{\texttt{1}} \ \ \color{blue}{\texttt{1}} \ \ \color{red}{\texttt{0}} & & 14: \ \ \ \ \color{orange}{\texttt{1}} \ \ \color{green}{\texttt{1}} \ \ \color{blue}{\texttt{1}} \ \ \color{red}{\texttt{0}} \\ 7: \ \ \ \ \color{orange}{\texttt{0}} \ \ \color{green}{\texttt{1}} \ \ \color{blue}{\texttt{1}} \ \ \color{red}{\texttt{1}} & & 15: \ \ \ \ \color{orange}{\texttt{1}} \ \ \color{green}{\texttt{1}} \ \ \color{blue}{\texttt{1}} \ \ \color{red}{\texttt{1}} \\ \end{align*} 0: 0 0 0 01: 0 0 0 12: 0 0 1 03: 0 0 1 14: 0 1 0 05: 0 1 0 16: 0 1 1 07: 0 1 1 18: 1 0 0 09: 1 0 0 110: 1 0 1 011: 1 0 1 112: 1 1 0 013: 1 1 0 114: 1 1 1 015: 1 1 1 1
可以看到每个位置的比特都在以特定的频率周期性变化,最低位每过一个数字就会变化一次,次低位每过两个数字就会变化一次,依次类推。
对于浮点数空间,使用二进制编码是极其浪费的。因此我们可以使用更适合浮点数空间的三角函数来引入周期性。在位置编码中,正弦余弦函数相当于二进制编码中的比特位,通过改变它们的频率,我们相当于控制了不同的比特位。
位置编码如何结合到词向量中
在 Transformer 中,位置编码是通过加法的方式结合到词向量中的,即对于一个句子 [ w 1 , . . . w n ] [w_1,...w_n] [w1,...wn] 中的第 t t t 个单词 w t w_t wt,Transformer 的输入为:
ψ ′ ( w t ) = ψ ( w t ) + p t ⃗ \begin{align*} \psi^\prime(w_t) = \psi(w_t) + \vec{p_t} \end{align*} ψ′(wt)=ψ(wt)+pt
其中 ψ ( w t ) \psi(w_t) ψ(wt) 为单词 w t w_t wt 的词向量, p t ⃗ \vec{p_t} pt 为单词 w t w_t wt 的位置编码。
由上式可知,位置编码的维度 d d d 必须与词向量的维度相同,这样才能保证它们可以相加。
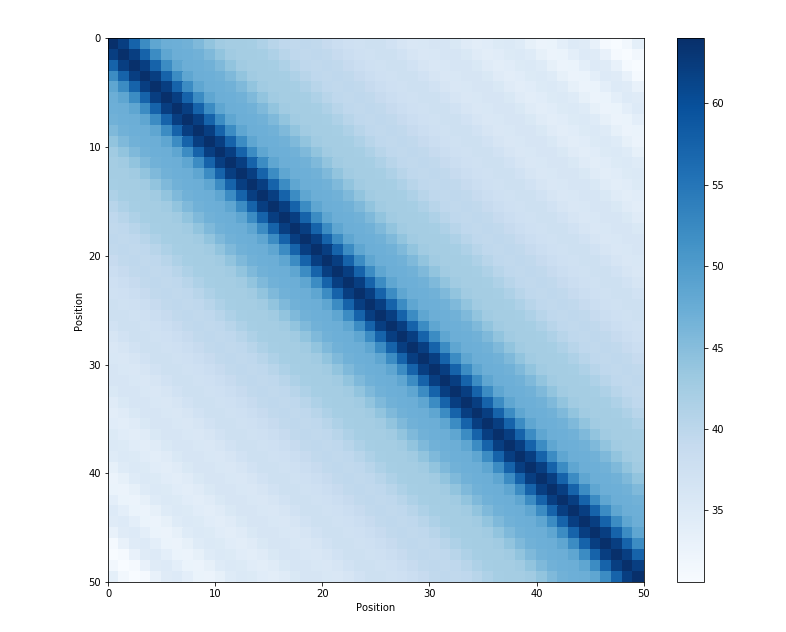
相对位置
正弦位置编码的另一个特点是,它能让模型更加轻松地捕捉到相对位置信息。下面是原论文中的一段话:
We chose this function because we hypothesized it would allow the model to easily learn to attend by relative positions, since for any fixed offset k k k, P E p o s + k PE_{pos+k} PEpos+k can be represented as a linear function of P E p o s PE_{pos} PEpos.
即对于任意固定的偏移量 k k k,位置编码 P E p o s + k PE_{pos+k} PEpos+k 总能被 P E p o s PE_{pos} PEpos 线性表示。
笔者水平有限,在这里就不进行证明了。
除此之外,正弦位置编码的另一个特点是,相邻时间步长之间的距离是对称的(正弦位置编码对距离的衡量是无向的),即 P E p o s ⋅ P E p o s + k = P E p o s ⋅ P E p o s − k PE_{pos} \cdot PE_{pos+k} = PE_{pos} \cdot PE_{pos-k} PEpos⋅PEpos+k=PEpos⋅PEpos−k
其他问题
为什么位置编码与词向量结合是使用相加而不是连接
首先,连接位置编码与词向量会提高输入的维度,这将提高模型的参数量。
其次,从前文的图中可以看出,位置编码的信息并不是均匀分布于每个维度之上,而是几乎所有的位置信息都分布在较低的维度之内(在原文中,词向量的维度为 512 512 512 维)。由于 Transformer 的 Word Embedding 层是重新训练的,因此可能 Word Embedding 层在训练过程中根本没有往靠前维度存储语义信息,以免干扰位置编码。在这种情况下, 512 512 512 维的位置编码与 512 512 512 维的词向量相加似乎就等价于 x x x 维的位置编码与 512 − x 512-x 512−x 维的词向量连接。
位置编码信息如何传递到模型深层
理论上,位置编码信息在经过自注意力机制层或者前馈神经网络层后,就会被丢失。但 Transformer 为各个网络层添加了残差连接,这使得位置编码信息可以通过残差链接来逐步传递到模型的深层。
为什么要同时使用正弦和余弦函数
只有同时使用正弦和余弦函数才能将 sin ( x + k ) \sin(x+k) sin(x+k) 和 cos ( x + k ) \cos(x+k) cos(x+k) 表示为 sin ( x ) \sin(x) sin(x) 和 cos ( x ) \cos(x) cos(x) 的线性变换,即位置编码 P E p o s PE_{pos} PEpos 一定要包含正弦和余弦函数才能线性表示 P E p o s + k PE_{pos+k} PEpos+k,这对模型捕获相对位置信息具有很大的帮助。
| Tiny-Vicuna-1B:Tiny Models轻量化系列Top One)






)



)





机器人栅格路径规划,输出做短路径图和适应度曲线。)

