day18 找树左下角的值路径总和路径总和Ⅱ 从中序与后序遍历序列构造二叉树从前序与中序遍历序列构造二叉树

题目1：513 找树左下角的值

题目链接：513 找树左下角的值

题意

找出二叉树的最底层最左边节点的值 (假设二叉树中至少有1个节点)

最底层节点确保是深度最大的叶子节点，最左边的节点却不一定是左孩子

递归遍历

深度最大的叶子节点最左侧的值，使用前序（中左右）中序（左中右）后序（左右中）遍历均可，因为都是先遍历左，后遍历右，这样确保先遍历左节点，如果左节点满足，就会直接放入result中，如果没有左节点，才会遍历同层的右节点这样保证遍历的是二叉树的深度最大的叶子节点的最左边的值

递归三部曲

1）确定递归函数的参数和返回值

2）确定终止条件

3）确定单层递归逻辑

代码

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode() : val(0), left(nullptr), right(nullptr) {}*     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}*     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:int maxdepth = INT_MIN;//记录最大深度int result = 0;//记录最大深度对应的节点数值void traversal(TreeNode* node,int depth){//终止条件  叶子节点if(node->left==NULL && node->right==NULL){if(maxdepth < depth){maxdepth = depth;result = node->val;}}//单层递归逻辑if(node->left){depth++;traversal(node->left,depth);depth--;//回溯}if(node->right){depth++;traversal(node->right,depth);depth--;//回溯}}int findBottomLeftValue(TreeNode* root) {int depth = 0;traversal(root,depth);return result; }
};

逻辑

如果右节点的值大于本层左节点的值，会改变result吗？

Answer：并不会

层序遍历

记录最后一层遍历到的第一个节点的值就可

代码

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode() : val(0), left(nullptr), right(nullptr) {}*     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}*     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:int findBottomLeftValue(TreeNode* root) {queue<TreeNode*> que;int result = 0;if(root!=NULL) que.push(root);while(!que.empty()){int size = que.size();for(int i=0;i<size;i++){TreeNode* node = que.front();que.pop();if(i==0) result = node->val;//记录每一层的第一个节点的值 直到更新到最后一层if(node->left) que.push(node->left);if(node->right) que.push(node->right);}}return result;}
};

题目2：112 路径总和

题目链接：112 路径总和

题意

判断是否存在：根节点到叶子节点的路径上所有节点值相加等于目标和targetsum

如果存在，返回true，如果不存在，返回false

递归

前序遍历，中序遍历，后序遍历均可，因为没有中节点的处理逻辑

递归三部曲：

1）确定递归函数的返回值和参数只要有1条路径就行，返回true 所以递归函数需要返回值

2）确定终止条件

3）确定单层递归逻辑

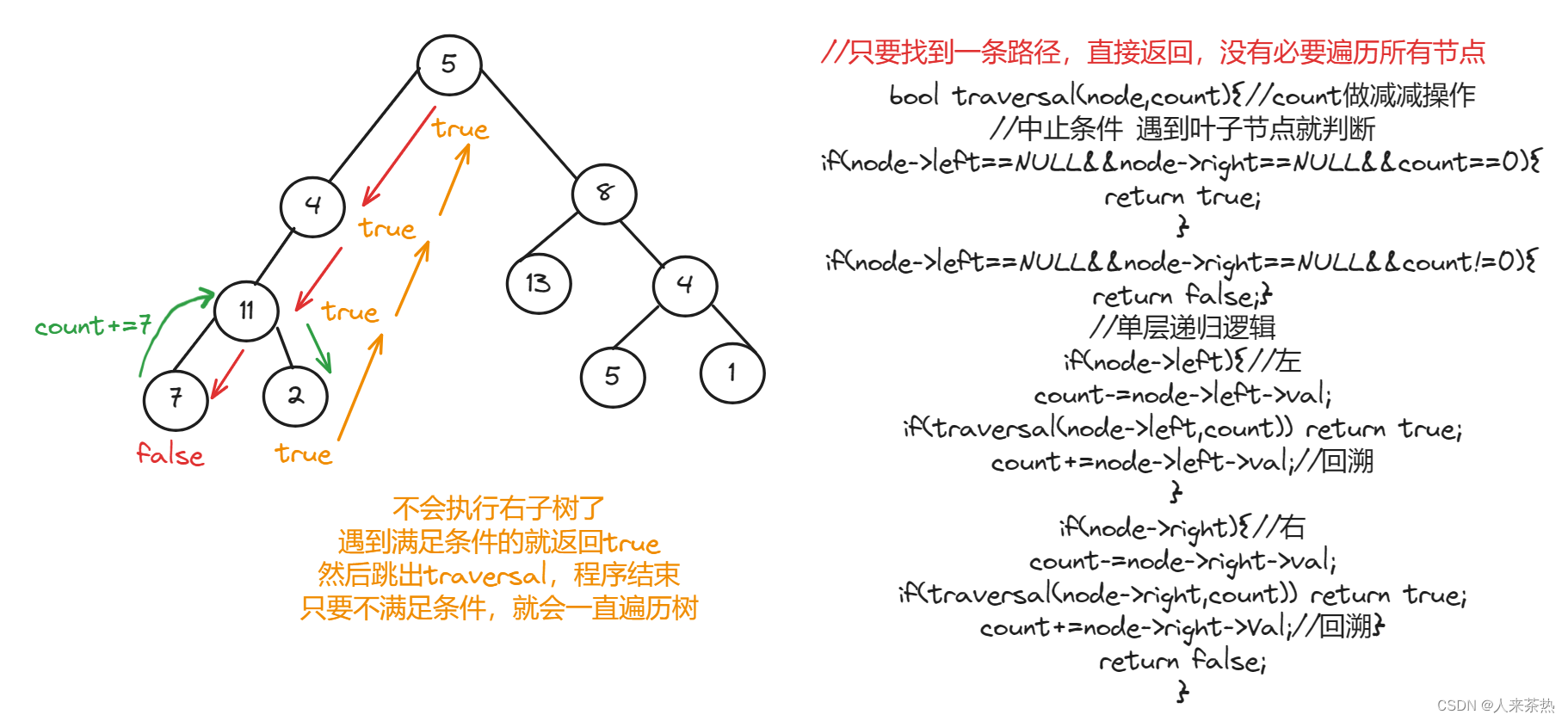
代码

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode() : val(0), left(nullptr), right(nullptr) {}*     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}*     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:bool traversal(TreeNode* node,int count){//终止条件  遇到叶子节点就判断一下if(node->left==NULL && node->right==NULL && count==0) return true;if(node->left==NULL && node->right==NULL && count!=0) return false;//单层递归逻辑if(node->left){count -= node->left->val;if(traversal(node->left,count)) return true;count += node->left->val;}if(node->right){count -= node->right->val;if(traversal(node->right,count)) return true;count += node->right->val;}return false;}bool hasPathSum(TreeNode* root, int targetSum) {if(root==NULL) return false;return traversal(root,targetSum-root->val);}
};

迭代遍历

使用栈的方法代替递归遍历栈中放入两个值：当前节点当前总和

代码

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode() : val(0), left(nullptr), right(nullptr) {}*     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}*     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:bool hasPathSum(TreeNode* root, int targetSum) {if(root==NULL) return false;stack<pair<TreeNode*,int>> st;st.push(pair<TreeNode*,int>(root,root->val));//st的第二个位置处的整数做加加操作while(!st.empty()){pair<TreeNode*,int> node = st.top();st.pop();if(node.first->left==NULL && node.first->right==NULL && node.second==targetSum) return true;if(node.first->right) st.push(pair<TreeNode*,int>(node.first->right,node.second+node.first->right->val));//左if(node.first->left) st.push(pair<TreeNode*,int>(node.first->left,node.second+node.first->left->val));//右}return false;}
};

题目3：113 路径总和Ⅱ

题目链接：路径总和Ⅱ

题意

找出所有根节点到叶子节点的路径总和等于targetsum的路径

递归遍历

要遍历所有的节点，所以递归函数不需要返回值

代码

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode() : val(0), left(nullptr), right(nullptr) {}*     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}*     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:vector<int> path;vector<vector<int>> result;void traversal(TreeNode* node,int count){//终止条件if(node->left==NULL && node->right==NULL && count==0){result.push_back(path);return;}//单层递归逻辑if(node->left){path.push_back(node->left->val);count -= node->left->val;traversal(node->left,count);count += node->left->val;path.pop_back();}if(node->right){path.push_back(node->right->val);count -= node->right->val;traversal(node->right,count);count += node->right->val;path.pop_back();}}vector<vector<int>> pathSum(TreeNode* root, int targetSum) {if(root==NULL) return result;path.push_back(root->val);traversal(root,targetSum-root->val);return result;}
};

迭代遍历较为复杂

题目4：106 从中序与后序遍历序列二叉构造树

题目链接：106 从中序遍历与后序遍历序列构造二叉树

题意

根据中序遍历数组inorder和后序遍历数组postorder构造二叉树

递归

递归三部曲：

1）确定递归函数的参数和返回值

2）确定终止条件

3）确定单层递归逻辑

数组

代码

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode() : val(0), left(nullptr), right(nullptr) {}*     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}*     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder) {//终止条件if(postorder.size()==0) return NULL;//单层递归逻辑//中节点int rootvalue = postorder[postorder.size()-1];TreeNode* root = new TreeNode(rootvalue);if(postorder.size()==1) return root;//叶子节点//寻找中序数组的切割点indexint index;for(index=0;index<inorder.size();index++){if(inorder[index]==rootvalue){break;}}//切割中序数组(左中右)  左闭右开  循环不变量//中序左vector<int> inorderleft(inorder.begin(),inorder.begin()+index);//中序右  //注意抛除掉中节点vector<int> inorderright(inorder.begin()+index+1,inorder.end());//切割后序数组(左右中)//去除掉中节点postorder.resize(postorder.size()-1);//后序左vector<int> postorderleft(postorder.begin(),postorder.begin()+inorderleft.size());//后序右vector<int> postorderright(postorder.begin()+inorderleft.size(),postorder.end());//左子树root->left = buildTree(inorderleft,postorderleft);//右子树root->right = buildTree(inorderright,postorderright);return root;}
};

下标（节省空间复杂度）

代码

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode() : val(0), left(nullptr), right(nullptr) {}*     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}*     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:TreeNode* traversal(vector<int>& inorder,int inorderbegin,int inorderend,vector<int>& postorder,int postorderbegin,int postorderend){//终止条件if(postorderbegin == postorderend) return NULL;//单层递归逻辑//中节点int rootvalue = postorder[postorderend-1];TreeNode* root = new TreeNode(rootvalue);if(postorderend-postorderbegin==1) return root;//中序数组切割点int index;for(index=inorderbegin;index<inorderend;index++){if(inorder[index]==rootvalue){break;}}//切割中序数组（左中右）  左闭右开//中序左int inorderleftbegin = inorderbegin;int inorderleftend = index;//注意使用的是索引的方法，所以这里直接使用索引//中序右  抛除掉中节点int inorderrightbegin = index + 1;int inorderrightend = inorderend;//切割后序数组（左右中）  左闭右开//后序左int postorderleftbegin = postorderbegin;int postorderleftend = postorderbegin + (inorderleftend - inorderleftbegin);//由于后序是通过中序左的的大小得到的，所以前面要加上postorderbegin//后序右  抛除掉中节点int postorderrightbegin= postorderbegin + (inorderleftend - inorderleftbegin);int postorderrightend = postorderend - 1;// cout<<"inorderleft:";//中序左// for(int i=inorderleftbegin;i<inorderleftend;i++){//     cout<<inorder[i]<<" ";// }// cout<<endl;// cout<<"inorderright:";//中序右// for(int j=inorderrightbegin;j<inorderrightend;j++){//     cout<<inorder[j]<<" ";// }// cout<<endl;// cout<<"postorderleft:";//后序左// for(int i=postorderleftbegin;i<postorderleftend;i++){//     cout<<postorder[i]<<" ";// }// cout<<endl;// cout<<"postorderright:";//后序右// for(int i=postorderrightbegin;i<postorderrightend;i++){//     cout<<postorder[i]<<" ";// }// cout<<endl;root->left = traversal(inorder,inorderleftbegin,inorderleftend,postorder,postorderleftbegin,postorderleftend);root->right = traversal(inorder,inorderrightbegin,inorderrightend,postorder,postorderrightbegin,postorderrightend);return root;}TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder) {//终止条件if(postorder.size()==0) return NULL;return traversal(inorder,0,inorder.size(),postorder,0,postorder.size());  //左闭右开}
};

题目5：105 从前序与中序遍历序列构造二叉树

题目链接：105 从前序与中序遍历序列构造二叉树

题意

根据前序遍历数组preorder和中序遍历数组inorder构造二叉树

递归

数组

代码

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode() : val(0), left(nullptr), right(nullptr) {}*     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}*     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) {//终止条件//空节点if(preorder.size()==0) return NULL;//单层递归逻辑//中节点int rootvalue = preorder[0];TreeNode* root = new TreeNode(rootvalue);if(preorder.size()==1) return root;//叶子节点//中序数组切割点int index;for(index=0;index<inorder.size();index++){if(inorder[index]==rootvalue){break;}}//切割中序数组(左中右)   左闭右开//中序左vector<int> inorderleft(inorder.begin(),inorder.begin()+index);//中序右   抛除掉中节点元素vector<int> inorderright(inorder.begin()+index+1,inorder.end());//切割前序数组(中左右)  左闭右开//抛除掉中节点元素//前序左vector<int> preorderleft(preorder.begin()+1,preorder.begin()+1+inorderleft.size());//前序右vector<int> preorderright(preorder.begin()+1+inorderleft.size(),preorder.end());root->left = buildTree(preorderleft,inorderleft);root->right = buildTree(preorderright,inorderright);return root;}
};

下标

代码

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode() : val(0), left(nullptr), right(nullptr) {}*     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}*     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:TreeNode* traversal(vector<int>& preorder, int preorderbegin, int preorderend, vector<int>& inorder,int inorderbegin, int inorderend){//终止条件if(preorderend-preorderbegin==0) return NULL;//单层递归逻辑//中节点int rootvalue = preorder[preorderbegin];TreeNode* root = new TreeNode(rootvalue);//叶子节点if(preorderend-preorderbegin==1) return root;//中序数组切割点int index;for(index=0;index<inorderend;index++){if(inorder[index]==rootvalue){break;}}//切割中序数组 左中右//中序左int inorderleftbegin = inorderbegin;int inorderleftend = index;//中序右  抛除中节点indexint inorderrightbegin = index + 1;int inorderrightend = inorderend;//切割前序数组  中左右//前序左  抛除中节点preorderbeginint preorderleftbegin = preorderbegin + 1;int preorderleftend = preorderbegin + 1 + (index - inorderbegin);//前序右  int preorderrightbegin = preorderbegin + 1 + (index - inorderbegin);int preorderrightend = preorderend;root->left = traversal(preorder,preorderleftbegin,preorderleftend,inorder,inorderleftbegin,inorderleftend);root->right = traversal(preorder,preorderrightbegin,preorderrightend,inorder,inorderrightbegin,inorderrightend);return root;}TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) {if(preorder.size()==0) return NULL;return traversal(preorder,0,preorder.size(),inorder,0,inorder.size());}
};