- 智能体学习（learning）：一个智能体通过对世界进行观测来提高它的性能
- 机器学习（machine learning）：智能体是一台计算机 —— 一台计算机观测到一些数据，基于这些数据构建一个模型（model），并将这个模型作为关于世界的一个假设（hypothesis）以及用于求解问题的软件的一部分
为什么希望一台机器进行学习？
- 程序的设计者无法预见未来所有可能发生的情形
- 有时候设计者并不知道如何设计一个程序来求解目标问题——大多数人都能辨认自己家人的面孔，但是他们实现这一点利用的是潜意识
1 学习的形式
- 归纳（induction）：从一组特定的观测结果得出一个普遍的规则—— 归纳的结论可能是不正确【只要前提是正确的，演绎（deduction）的结论就保证是正确的】
- 分类（classification）：输出是一个有限集合中的某个值时
- 回归（regression）：输出是一个数值
根据输入有3种类型的反馈（feedback），学习可分为3类：
- 监督学习（supervised learning）：智能体观测到输入-输出对，并学习从输入到输出的一个函数映射 —— 输出称之为标签（label）
- 无监督学习（unsupervised learning）：智能体从没有任何显式反馈的输入中学习模式；最常见的无监督学习任务是聚类（clustering）
- 强化学习（reinforcement learning）中：智能体从一系列的强化——奖励与惩罚——中进行学习，智能体判断之前采取的哪个动作该为这一结果负责，并且改变它的动作以在未来得到更多的奖励
2 监督学习
监督学习的任务：
- 给定一个训练集（training set）含有N个“输入-输出”对样例： ( x 1 , y 1 ) , ( x 2 , y 2 ) , ( x 3 , y 3 ) , . . . , ( x N , y N ) (x_1,y_1),(x_2,y_2),(x_3,y_3),...,(x_N,y_N) (x1,y1),(x2,y2),(x3,y3),...,(xN,yN)
- 每一对数据都由一个未知的函数 y = f ( x ) y=f(x) y=f(x)生成
- 目标：寻找一个函数 h h h来近似真实的函数 f f f
- 函数 h h h ：关于世界的假设（hypothesis），取自一个包含所有可能的函数 假设空间（hypothesis space） H \mathcal{H} H【其他说法，模型-模型类，函数-函数类】
- 输出 y i y_i yi：真实数据（ground truth）
如何选择一个假设空间
- 关于数据生成过程的先验知识【如果有的话】
- 采用探索性数据分析（exploratory data analysis）：通过统计检验和可视化方法——直方图、散点图、箱形图——来探索数据以获得对数据的一些理解，以及洞察哪些假设空间可能是合适的
- 直接尝试多种不同的假设空间，然后评估哪个假设空间的效果最好
如何从假设空间中选择一个好的假设
- 寻找一个一致性假设（consistent hypothesis）：假设 h h h ，对训练集中的任意一个 x i x_i xi，都有 h ( x i ) = y i h(x_i) = yi h(xi)=yi
- 如果输出是连续值，不能期望模型输出与真实数据精确匹配,而是寻找一个最佳拟合函数（best-fit function），使得每一个 h ( x i ) h(x_i) h(xi)与 y i y_i yi非常接近
- 衡量一个假设的标准不是看它在训练集上的表现，而是取决于它如何处理尚未观测到的输入：使用一个测试集（test set）—— 如果 h h h 准确地预测了测试集的输出，称 h h h 具有很好的泛化（generalize）能力
如何分析假设空间：
- 偏差（bias）：（不严格地）在不同的训练集上，假设所预测的值偏离期望值的平均趋势：
- 常常是由假设空间所施加的约束造成的，如假设空间是线性函数时会导致较大的偏差，分段线性函数具有较小的偏差
- 欠拟合（underfitting）：一个假设不能找到数据中的模式
- 方差（variance）：由训练数据波动而导致假设的变化量
- 过拟合（overfitting）：一个函数过于关注它用来训练的特定训练数据集，进而导致它在没有见过的数据上表现较差
- 偏差-方差权衡（bias-variance tradeoff）：在更复杂、低偏差的能较好拟合训练集的假设与更简单、低方差的可能泛化得更好的假设中做出选择
- 奥卡姆剃刀原则（Ockham’s razor）：如无必要，勿增实体
表达能力与复杂性的权衡：
- 表达性语言使简单的假设能够与数据相匹配
- 限制语言的表达能力则意味着任何一致性假设都必定是复杂的
3 决策树学习
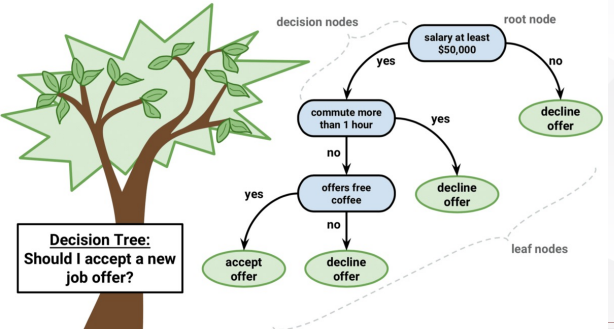
决策树（decision tree）：将属性值向量映射到单个输出值（即“决策”）的函数
- 决策树通过执行一系列测试来实现其决策：从根节点出发，沿着适当的分支，直到到达叶节点为止
- 树中的每个内部节点对应于一个输入属性的测试，该节点的分支用该属性的所有可能值进行标记，叶节点指定了函数要返回的值
3.1 决策树的表达能力
- 命题逻辑中的任何函数都可以表示为决策树
一棵布尔型的决策树的逻辑语句：
-
O u t p u t ⇔ （ P a t h 1 ∨ P a t h 2 ∨ … ） Output \Leftrightarrow （Path_1 \vee Path_2 \vee …） Output⇔（Path1∨Path2∨…）
-
P a t h i Path_i Pathi：根节点到true叶节点的路径上的属性-值测试形式 A m = v x ∧ A n = v y ∧ … ） A_m = v_x \wedge A_n = v_y \wedge …） Am=vx∧An=vy∧…）的合取
-
所有的决策树将空间分割为矩形，即与坐标轴平行的方框
-
不存在一种表示方式使得任何函数都能被有效地表示
最重要的属性：对一个样例的分类结果能产生最大影响的属性
