将强化学习与机器学习、深度学习区分开的最重要的特征为:它通过训练中信息来评估所采取的动作,而不是给出正确的动作进行指导,这极大地促进了寻找更优动作的需求。
1、多臂老虎机(Multi-armed Bandits)问题
赌场的老虎机有一个绰号叫单臂强盗(single-armed bandit),因为它即使只有一只胳膊,也会把你的钱拿走。而一排老虎机就引申出多臂强盗(多臂老虎机)。
多臂老虎机(Multi-armed Bandits)问题可以描述如下:一个玩家走进一个赌场,赌场里有 k k k 个老虎机,每个老虎机的期望收益不一样。假设玩家总共可以玩 t t t 轮, 在每一轮中,玩家可以选择这 k k k 个老虎机中的任一个,投入一枚游戏币,拉动摇杆,观察是否中奖以及奖励的大小。
问题,玩家采取怎么样的策略才能最大化这 t t t 轮的总收益?
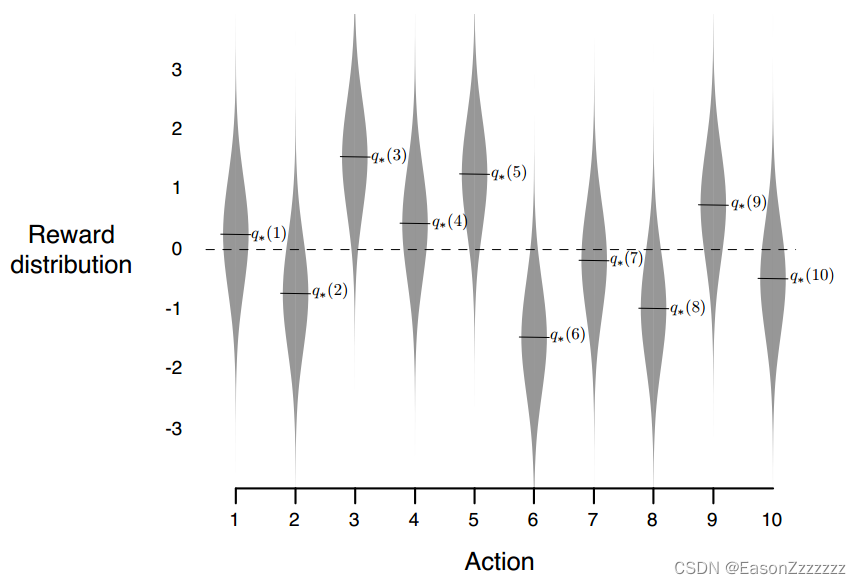
k k k 个老虎机(对应 k k k 个动作选择),每一个动作都有其预期的奖励,称其为该动作的价值。记第 t t t 轮选择的动作为 A t A_t At,相应的奖励为 R t R_t Rt,那么任意动作 a a a 的价值记为 q ∗ ( a ) q_\ast(a) q∗(a),即动作 a a a 的期望奖励:
q ∗ ( a ) ≐ E [ R t ∣ A t = a ] q_\ast(a)\doteq\Bbb{E}[R_t|A_t=a] q∗(a)≐E[Rt∣At=a]
如果知道每个动作的价值,那么问题就简单了:总是选择价值最高的动作。如果不知道的话,我们需要对其进行估计,令动作 a a a 在时间步长为 t t t 的价值估计为 Q t ( a ) Q_t(a) Qt(a),我们希望 Q t ( a ) Q_t(a) Qt(a) 尽可能地接近 q ∗ ( a ) q_\ast(a) q∗(a)。
2、动作价值方法
通过估计动作价值,然后依据动作价值作出动作选择的方法,统称为动作价值方法。某个动作的真实价值应当是该动作被选择时的期望奖励,即
Q t ( a ) ≐ t 时刻之前, a 被选中的总奖励 t 时刻之前, a 被选中的次数 = ∑ i = 1 t − 1 R i ⋅ I A i = a ∑ i = 1 t − 1 I A i = a Q_t(a)\doteq\dfrac{t\ 时刻之前,a\ 被选中的总奖励}{t\ 时刻之前,a\ 被选中的次数}=\dfrac{\sum_{i=1}^{t-1}R_i\cdot\Bbb{I}_{A_i=a}}{\sum_{i=1}^{t-1}\Bbb{I}_{A_i=a}} Qt(a)≐t 时刻之前,a 被选中的次数t 时刻之前,a 被选中的总奖励=∑i=1t−1IAi=a∑i=1t−1Ri⋅IAi=a
其中,若 A i = a A_i=a Ai=a,则 I A i = a = 1 \Bbb{I}_{A_i=a}=1 IAi=a=1,否则 I A i = a = 0 \Bbb{I}_{A_i=a}=0 IAi=a=0,若分母为 0,则定义 Q t ( a ) Q_t(a) Qt(a) 为一默认值(例如 0),根据大数定律,当分母趋于无穷时, Q t ( a ) Q_t(a) Qt(a) 收敛于 q ∗ ( a ) q_\ast(a) q∗(a),称这种方法为样本平均法(sample-average method),这是估计动作价值的一种方法,当然并不一定是最好的方法,下面我们使用该方法来解决问题。
最简单的动作选择就是选择价值估计值最大的动作,称为贪心方法,其数学表示为:
A t ≐ arg max a Q t ( a ) A_t\doteq\argmax_a Q_t(a) At≐aargmaxQt(a)
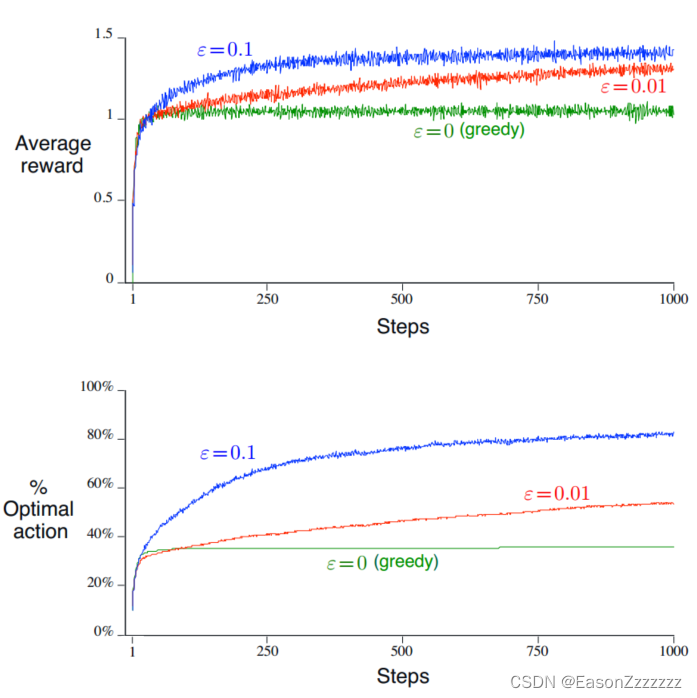
另一种替代的方法是,大多数情况是贪心的,偶尔从动作空间中随机选择,称为 ϵ \epsilon ϵ -贪心方法。这种方法的优点是,随着步数增加,每个动作会被无限采样,则 Q t ( a ) Q_t(a) Qt(a) 会逐渐收敛到 q ∗ ( a ) q_\ast(a) q∗(a),也意味着选择最优动作的概率收敛到 1 − ϵ 1-\epsilon 1−ϵ。
3、贪心动作价值方法有效性
在 2000 个随机生成的 10 臂老虎机问题中,其动作价值 q ∗ ( a ) , a = 1 , ⋯ , 10 q_\ast(a),a=1,\cdots,10 q∗(a),a=1,⋯,10,服从期望为 0,方差为 1的正态分布;另外每次动作 A t A_t At 的实际奖励 R t R_t Rt 服从期望为 q ∗ ( A t ) q_\ast(A_t) q∗(At) ,方差为 1 的正态分布。
部分代码
import numpy as npstep = 1000
q_true = np.random.normal(0, 1, 10) # 真实的动作价值
q_estimate = np.zeros(10) # 估计的动作价值
epsilon = 0.9 # 贪心概率
action_space = [0, 1, 2, 3, 4, 5, 6, 7, 8, 9]
action_count = np.zeros(10)
reward_sum = 0
for i in range(step):if (np.random.uniform() > epsilon1) or (q_estimate1.all() == 0):machine_name = np.random.choice(action_space)reward_sum += np.random.normal(q_true[machine_name], 1, 1)action_count[machine_name] += 1q_estimate[machine_name] = reward_sum / action_count[machine_name]else:machine_name = np.argmax(q_estimate)reward_sum += np.random.normal(q_true[machine_name], 1, 1)action_count[machine_name] += 1q_estimate[machine_name] = reward_sum / action_count[machine_name]
)










 》)







