.

个人主页：晓风飞
专栏：数据结构|Linux|C语言
路漫漫其修远兮，吾将上下而求索

---

---

引言

在数据结构中，二叉树因其在搜索、排序和平衡等操作中的高效性而显得尤为重要。在这篇博客文章中，我们将深入探讨二叉树的概念，探索它们在C语言中的实现，并了解它们的实际应用。

结构定义

在C语言中，可以使用结构来表示二叉树，定义数据以及指向左右子节点的指针：

typedef char BTDataType;typedef struct BinaryTreeNode
{BTDataType _data;struct BinaryTreeNode* _left;struct BinaryTreeNode* _right;
}BTNode;

---

接口需求

// 通过前序遍历的数组"ABD##E#H##CF##G##"构建二叉树
BTNode* BinaryTreeCreate(BTDataType* a, int n, int* pi);
// 二叉树销毁
void BinaryTreeDestory(BTNode** root);
// 二叉树节点个数
int BinaryTreeSize(BTNode* root);
// 二叉树叶子节点个数
int BinaryTreeLeafSize(BTNode* root);
// 二叉树第k层节点个数
int BinaryTreeLevelKSize(BTNode* root, int k);
// 二叉树查找值为x的节点
BTNode* BinaryTreeFind(BTNode* root, BTDataType x);
// 二叉树前序遍历 
void BinaryTreePrevOrder(BTNode* root);
// 二叉树中序遍历
void BinaryTreeInOrder(BTNode* root);
// 二叉树后序遍历
void BinaryTreePostOrder(BTNode* root);
// 层序遍历
void BinaryTreeLevelOrder(BTNode* root);
// 判断二叉树是否是完全二叉树
int BinaryTreeComplete(BTNode* root);

---

构建二叉树

//通过前序遍历的数组"ABD##E#H##CF##G##"构建二叉树
BTNode* BinaryTreeCreate(BTDataType* a, int n, int* pi)
{if (a[(*pi)] == '#'  || *pi > n)  //判断是否遍历完成或者遇到#，都返回NULL{(*pi)++;return NULL;}BTNode* root = (BTNode*)malloc(sizeof(BTNode)); // 创建新节点root->_data = a[*pi]; // 设置节点数据(*pi)++;root->_left = BinaryTreeCreate(a, n, pi); // 递归构建左子树root->_right = BinaryTreeCreate(a, n, pi); // 递归构建右子树return root;
}

---

销毁二叉树

// 二叉树销毁
void BinaryTreeDestory(BTNode** root)
{	if(*root == NULL)return NULL;BinaryTreeDestory(*root->left);BinaryTreeDestory(*root->right);free(*root);
}

---

计算节点和叶子的数量

二叉树节点个数

// 二叉树节点个数
int BinaryTreeSize(BTNode* root)
{return root == NULL ? 0 : BinaryTreeSize(root->_left) + BinaryTreeSize(root->_right) + 1;
}

二叉树叶子节点个数

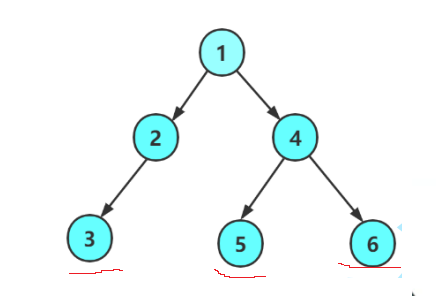
叶节点：位于树底部的节点，没有子节点，就像树上的叶子。

// 二叉树叶子节点个数
int BinaryTreeLeafSize(BTNode* root)
{if (root == NULL)return 0;if (root->_left == NULL  && root->_right == NULL)return 1;return BinaryTreeLeafSize(root->_left) + BinaryTreeLeafSize(root->_right);
}

二叉树第k层节点个数

// 二叉树第k层节点个数
int BinaryTreeLevelKSize(BTNode* root, int k)
{if (root == NULL || k < 1)return 0;if (k == 1)return 1;return BinaryTreeLevelKSize(root->_left, k - 1) + BinaryTreeLevelKSize(root->_right, k - 1);
}

---

二叉树查找值为x的节点

// 二叉树查找值为x的节点
BTNode* BinaryTreeFind(BTNode* root, BTDataType x)
{// 如果当前节点为空，返回 NULL。这意味着我们已经到达树的末端或者树本身为空。if (root == NULL)return NULL;// 如果当前节点的值等于要查找的值 x，返回当前节点的指针。if (root->_data == x)printf("找到了它是：%c",root->_data);elseprintf("没有找到！", root->_data);return root;// 在左子树中递归查找值为 x 的节点。BTNode* leftResult = BinaryTreeFind(root->_left, x);// 如果在左子树中找到了这个值，返回该节点的指针。if (leftResult != NULL)return leftResult;// 如果左子树中没有找到，继续在右子树中递归查找。return BinaryTreeFind(root->_right, x);
}

---

二叉树的遍历

遍历是二叉树中的一个关键操作，允许我们按特定顺序访问每个节点：

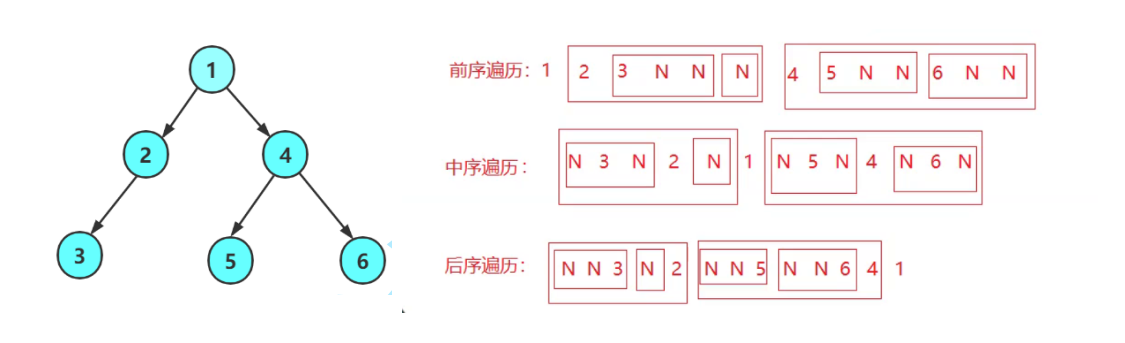
前序遍历：遍历顺序是根节点，左子树，右子树。
中序遍历：遍历顺序是左子树，根节点，右子树。
后序遍历：遍历顺序是左子树，右子树，根节点。

二叉树前序遍历

// 二叉树前序遍历 
void BinaryTreePrevOrder(BTNode* root)
{if (root == NULL)return NULL;printf("%c ", root->_data);BinaryTreePrevOrder(root->_left);BinaryTreePrevOrder(root->_right);
}

前序遍历首先访问根节点，然后递归地遍历左子树和右子树。这种遍历方法首先处理当前节点，然后处理子节点。

二叉树中序遍历

// 二叉树中序遍历
void BinaryTreeInOrder(BTNode* root)
{if (root == NULL)return NULL;BinaryTreeInOrder(root->_left);printf("%c ", root->_data);BinaryTreeInOrder(root->_right);
}

中序遍历首先递归地遍历左子树，然后访问根节点，最后遍历右子树。这对于二叉搜索树来说，可以按顺序访问所有节点。

二叉树后序遍历

// 二叉树后序遍历
void BinaryTreePostOrder(BTNode* root)
{if (root == NULL)return NULL;BinaryTreePostOrder(root->_left);BinaryTreePostOrder(root->_right);printf("%c ", root->_data);
}

后序遍历先递归地遍历左子树和右子树，最后访问根节点。这种遍历方法通常用于先处理子节点，然后再处理父节点的场景，如在二叉树中释放或删除节点。

二叉树层序遍历

// 二叉树层序遍历
void BinaryTreeLevelOrder(BTNode* root) 
{if (root == NULL) return; // 如果树为空，则直接返回Queue q;QInit(&q); // 初始化队列QPush(&q, root); // 将根节点入队while (!QueueEmpty(&q)){BTNode* front = QueueFront(&q); // 取得队首元素QPop(&q); // 将队首元素出队// 处理当前节点，例如打印节点的值printf("%c ", front->_data);if (front->_left != NULL) {QPush(&q, front->_left); // 将左子节点入队}if (front->_right != NULL) {QPush(&q, front->_right); // 将右子节点入队}}QDestroy(&q); // 销毁队列，释放资源
}

层序遍历使用队列来迭代地访问每一层的所有节点，从根节点开始，依次遍历每一层的左右子节点。这种遍历方法可以确保按照树的层次顺序访问每个节点，从上到下，从左到右。

深度优先遍历（DFS）

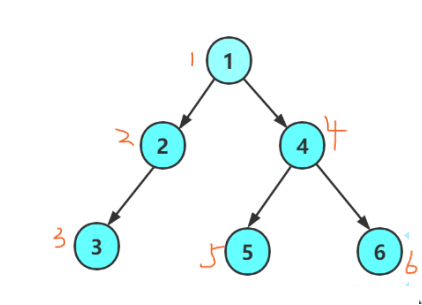
遍历方式：DFS 从根节点开始，沿着树的深度向下遍历，直到没有子节点可以访问，然
后回溯到上一个节点，继续遍历未探索的分支。这个过程一直重复，直到访问了所有可达的节点。

使用的数据结构：通常使用栈（Stack）来实现，这可以是递归实现的隐式栈（函数调用栈）或显式的数据结构栈。

特点：DFS 能够深入到树的底部，但可能会在树的某一分支上“走得太远”，尤其是在处理具有大量节点和深层次结构的树时。

应用场景：DFS 更适用于目标路径较深或树的结构不规则的情况。在图论中，DFS 常用于拓扑排序和检查图中的环。

以下是遍历顺序：

广度优先遍历（BFS）

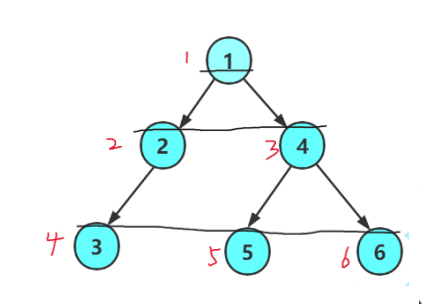
遍历方式：BFS 从根节点开始，先遍历根节点的所有邻接节点，然后再遍历这些邻接节点的邻接节点，以此类推。BFS 逐层遍历树的节点，从根节点开始向外扩散。

使用的数据结构：通常使用队列（Queue）来实现。遍历过程中，先进入队列的节点先遍历，确保了节点是按照层级顺序访问的。

特点：BFS 能够快速访问到从根节点开始的每一层节点，但在宽度较大的树或图中，可能会消耗更多的内存。

应用场景：BFS 更适用于目标节点离根节点比较近或需要按层次遍历的情况。在图论中，BFS 常用于寻找最短路径。

总结来说，DFS 优先沿着树的深度遍历，直到遇到叶子节点，然后回溯并探索其他分支，而 BFS 优先遍历距离根节点最近的节点，逐层向外扩展。两者在解决不同类型的问题时各有优势。DFS 在树的深度较大时更有效，而 BFS 在寻找最短路径或树的宽度较大时更有优势。

以下是遍历顺序

---

判断二叉树是否是完全二叉树

// 判断二叉树是否是完全二叉树
int BinaryTreeComplete(BTNode* root) {if (root == NULL) {return 1; // 空树认为是完全二叉树}Queue q;QInit(&q);QPush(&q, root);int level = 0; // 记录层级bool mustBeLeaf = false; // 标记是否必须为叶子节点while (!QueueEmpty(&q)) {int size = QueueSize(&q); // 当前层的节点数level++;for (int i = 0; i < size; i++) {BTNode* front = QueueFront(&q);QPop(&q);// 如果标记为必须是叶子节点，但当前节点不是叶子节点，则不是完全二叉树if (mustBeLeaf && (front->_left != NULL || front->_right != NULL)) {return 0;}// 如果当前节点有右孩子但没有左孩子，则不是完全二叉树if (front->_left == NULL && front->_right != NULL) {return 0;}if (front->_left != NULL) {QPush(&q, front->_left);}else {// 如果左孩子为空，则后面的节点都必须是叶子节点mustBeLeaf = true;}if (front->_right != NULL) {QPush(&q, front->_right);}else {// 如果右孩子为空，则后面的节点都必须是叶子节点mustBeLeaf = true;}}}QDestroy(&q);return 1; // 遍历结束没有发现违反完全二叉树的规则，返回1
}

这个函数用来判断一个二叉树是否是完全二叉树。它通过层序遍历来实现，检查每个节点是否符合完全二叉树的性质：如果某个节点的右子节点存在，而左子节点不存在，则不是完全二叉树；如果某个节点的左子节点或右子节点不存在，则该节点后的所有节点必须是叶子节点。

实际应用

二叉树不仅仅是理论构造，它们在现实世界中有着广泛的应用：

数据库系统：在索引中使用，实现高效的数据检索。
文件系统：用于组织文件的层级结构。
网络路由算法：帮助优化数据包的传输路径。

完整代码

可以来我的github参观参观，看完整代码
路径点击这里–>数据结构二叉树的实现

结论

通过深入了解和实现二叉树，我们不仅能够提高我们的编程技能，还能更好地理解这些结构在现代计算中的重要性。无论是在学术研究还是实际应用中，二叉树都是一个值得掌握的关键概念。