文章目录
- 概念
- 思路
- 绝对映射:
- 相对映射
- 代码实现
- 特性
- 结果演示
概念
计数排序是一个非基于比较的排序算法,该算法于1954年由 Harold H. Seward 提出。它的优势在于在对一定范围内的整数排序时,它的复杂度为Ο(n+k)(其中k是整数的范围),快于任何比较排序算法。 [1] 当然这是一种牺牲空间换取时间的做法,而且当O(k)>O(nlog(n))的时候其效率反而不如基于比较的排序(基于比较的排序的时间复杂度在理论上的下限是O(nlog(n)), 如归并排序,堆排序)
思路
- 统计相同元素出现次数
- 根据统计的结果将序列回收到原来的序列中
绝对映射:
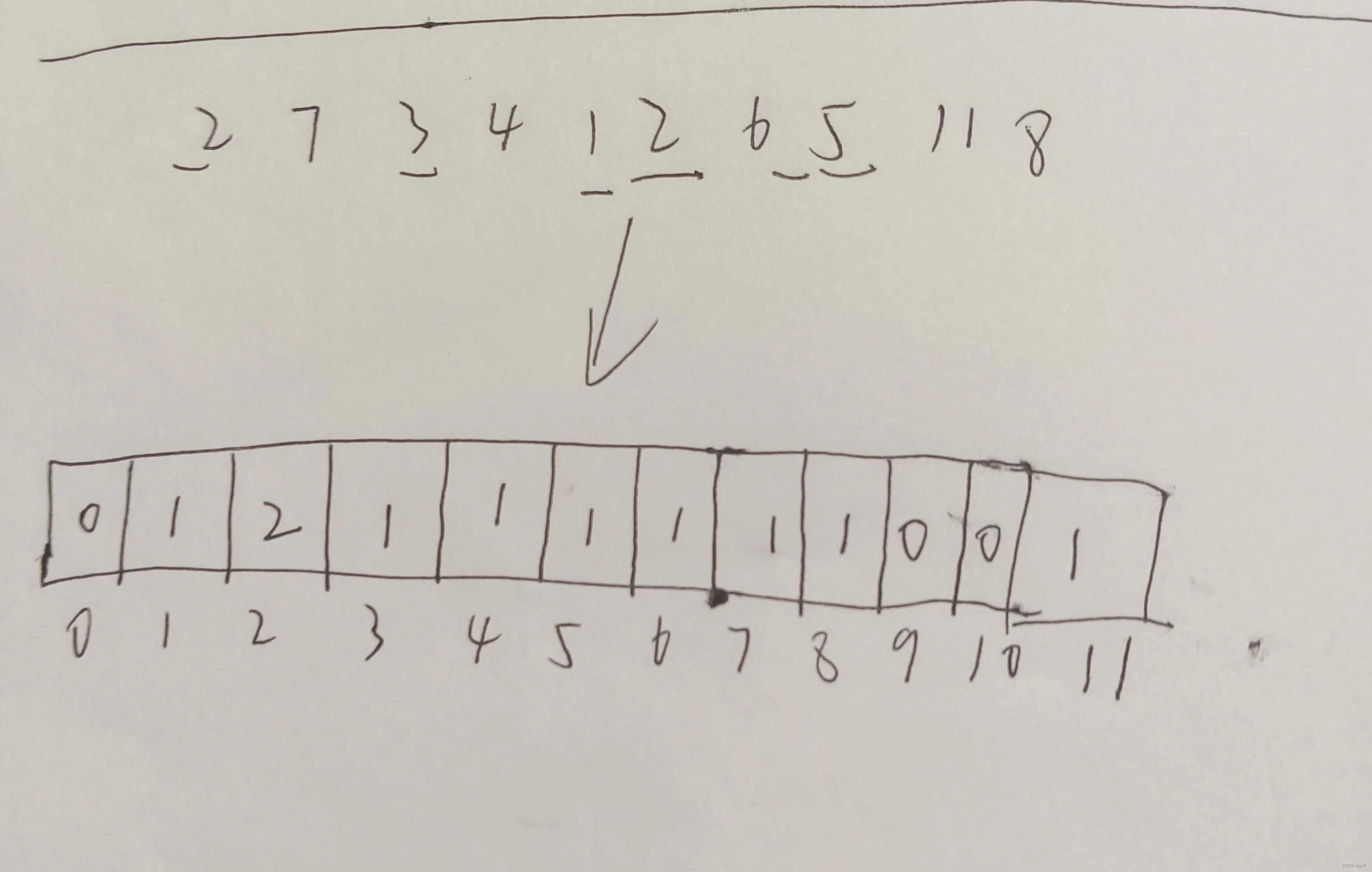
要排序的数字是多少,对应存放的下标就是多少。
相对映射
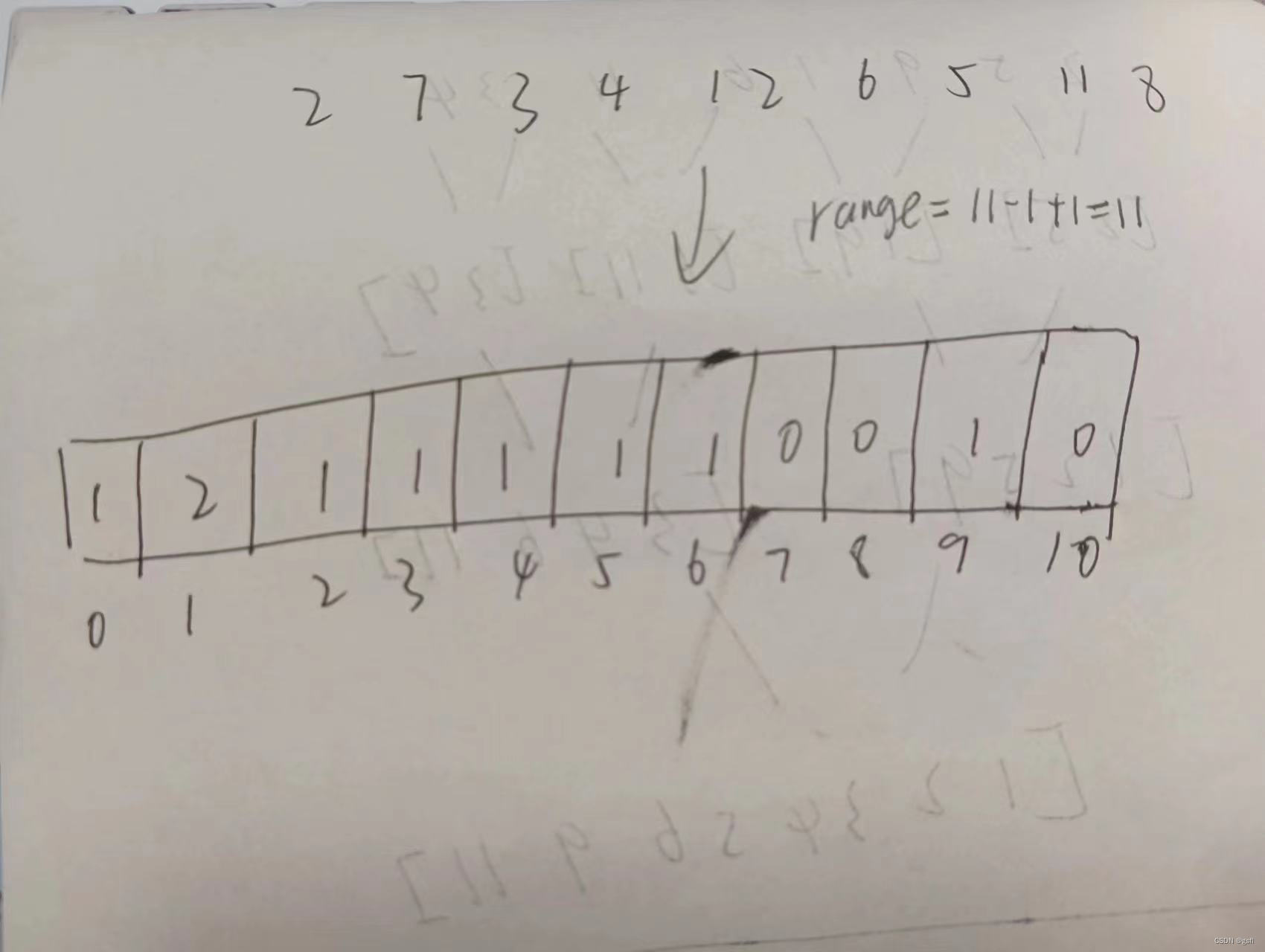
使最小数据和0下标对应,其他数据-最小数据=该数据对应下标。
相对映射解决了决定映射不能存放负数和元素很大时浪费空间的缺点。
代码实现
void CountSort(int* a, int n)
{int min = a[0], max = a[0];for (int i = 0; i < n; i++){if (a[i] < min){min = a[i];}if (a[i] > max){max = a[i];}}int range = max - min + 1;//找出最大最小值确定映射的范围int* count = (int*)calloc(range, sizeof(int));//用calloc可以把count数组初始化为0,方便后续计数统计for (int i = 0; i < n; i++){count[a[i] - min]++;}int i = 0;for (int j = 0; j < range; j++){while (count[j]--){a[i++] = j + min;//相对映射时减去了min,这里加上min得出原来的数据}}
}
特性
- 计数排序在数据范围集中时,效率很高,但是适用范围及场景有限。
- 时间复杂度:O(MAX(N,范围))
- 空间复杂度:O(范围)
- 稳定性:稳定
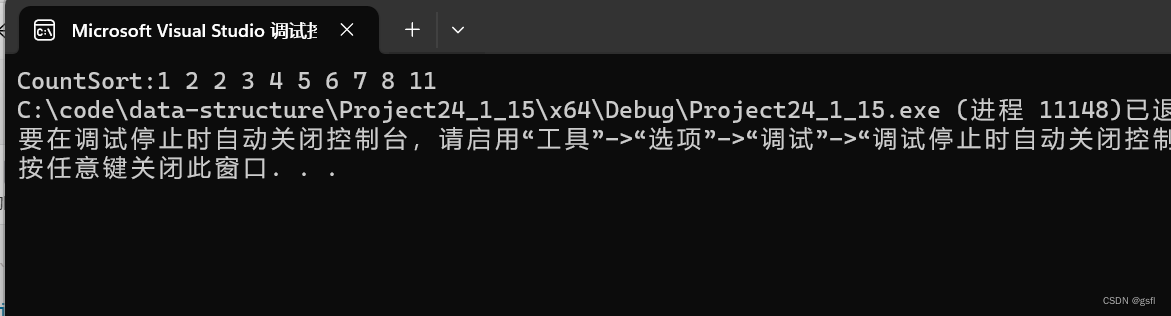
结果演示
int main()
{int b[] = { 2,7,3,4,1,2,6,5,11,8 };int n2 = sizeof(b) / sizeof(b[0]);CountSort(b, n2);
printf("CountSort:");for (int i = 0; i < n2; i++){printf("%d ", b[i]);}return 0;
}
![内网穿透[让你在家里也能榨干学校的服务器]Yep!](http://pic.xiahunao.cn/内网穿透[让你在家里也能榨干学校的服务器]Yep!)

4个技巧和靶场实战)






自定义字典及分词器)
:Passthrough 透视配置)


)


)
】螺旋数字矩阵(JavaPythonC++JS实现))

