适用平台：Matlab+Yalmip+Cplex/Gurobi；

文章提出了一种电动汽车充电站的两阶段规划方法，第一阶段通过蒙特卡洛法模拟充电车辆需求和电池充放电数据来确定充电站位置；第二阶段通过数据驱动的分布鲁棒优化方法优化充电站的新能源和电池容量。程序中算例丰富、注释清晰、干货满满，创新性很高！下面对文章和程序做简要介绍！

文章创新点：

数据驱动; 电动汽车充电站位置及容量规划； 两阶段分布鲁棒优化; 公路交通流量及充电需求; 新能源发电及容量规划

主要工作：

文中提出了一种电动汽车充电站的选址和容量两阶段规划方法。在第一阶段，通过交通需求和电池数据的蒙特卡洛模拟获得车辆需要充电服务的位置；，从潜在的候选充电站中确定充电站的最佳位置，确保每辆车都能在不耗尽电池的情况下访问至少一个充电站；提出了可以模拟充电站充电需求的时-空分布整数规划模型。在第二阶段，建立了基于数据驱动的分布式鲁棒优化模型，以优化充电站中可再生能源发电和储能单元的容量。不确定的发电量和需求由一组基于经验的不精确分布来描述，并且在Kullback–Leibler散度意义上，它们的距离由可调节的标量控制。提出了基于风险理论-稳健模型的两种重构方法。第一种方法依赖于风险值（VaR），并产生了更准确的混合整数线性规划（MILP）；第二中方法提供了一个基于条件VaR的保守近似，并归结为一个更易于处理的线性方案。

文章框架：

 

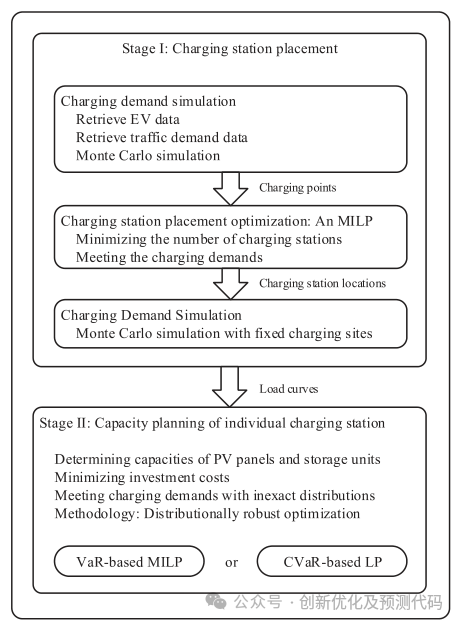
 文章结果：

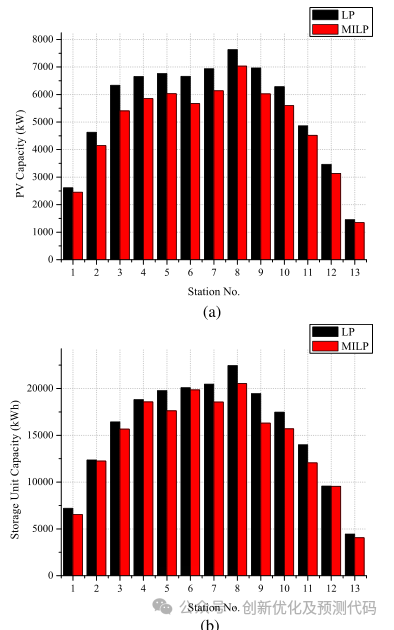
程序结果：

 

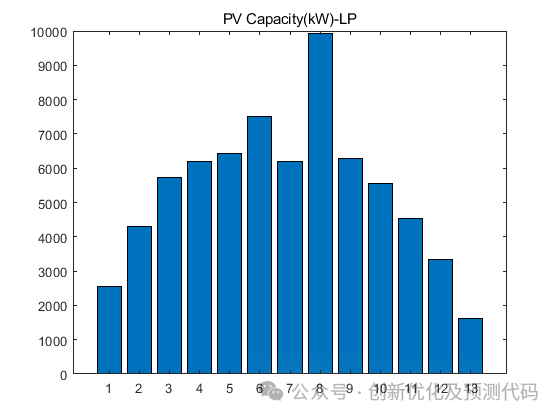
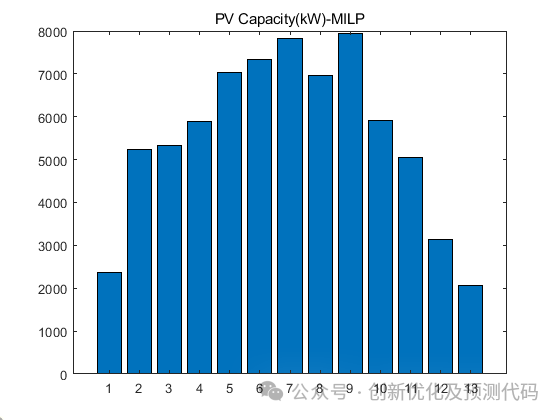
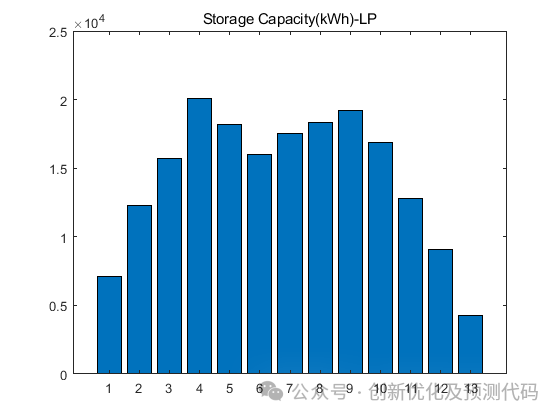
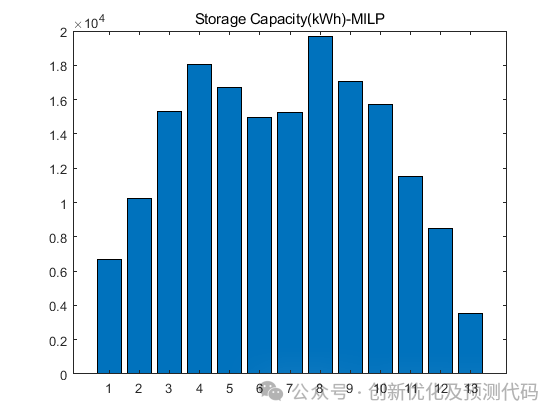
 部分程序：

 %% 优化
% 变量
x_1 = sdpvar(1, 1); % 定义光伏变量
x_2 = sdpvar(1, 1); % 定义充电站变量% w_0 = sdpvar(1, 1);
p_1 = sdpvar(T, q); % 新能源出力
p_2 = sdpvar(T, q); % 储能充放电
p_3 = sdpvar(T, q); % 电动汽车充放电f = sdpvar(q, 1);
g = sdpvar(q, 1);
gamma = sdpvar(1, 1);% 目标函数
Objective = Pr_1 * x_1 + Pr_2 * x_2; % 运行成本% 约束
Constraint1 = [x_1 >= 0, x_2 >= 0,  w_0 >= 0]; % 新能源、光伏约束Constraint2 = [];
for i = 1: qConstraint2 = [Constraint2, p_1(:, i) >= 0, p_2m * x_2 >= p_2(:, i) >= 0, p_3m * x_2 >= p_3(:, i) >= 0]; %设备出力约束
endallonestril = tril(ones(T));
Constraint3 = [];
for i = 1: qConstraint3 = [Constraint3, w_l * x_2 * ones(T, 1) <= w_0 * x_2 + allonestril * (eta_1 * p_2(:, i) - 1 / eta_2 * p_3(:, i)) * delta_t <= w_h * x_2 * ones(T, 1)]; %文中公式
endConstraint4 = [];
for i = 1: qConstraint4 = [Constraint4, sum(eta_1 * p_2(:, i) - 1 / eta_2 * p_3(:, i)) == 0 ];% 文中公式
endConstraint5 = [];Constraint6 = [];
for k = 1: qConstraint6 = [Constraint6, p_1(:, k) + p_2(:, k)  - xi_1(:, k) * x_1 <= 0]; %文中公式
endConstraint7 = [];
for k = 1: qConstraint7 = [Constraint7, xi_2(:, k) - p_1(:, k) - p_3(:, k) - f(k) <= 0]; % 文中公式
end
Constraint8 = [g >= f - gamma * ones(q, 1)];Constraint9 = [g >= 0];Constraint10 = [gamma + 1 / q / alpha_h * sum(g) <= 0];Constraints = [Constraint1, Constraint2, Constraint3, Constraint4, Constraint5, Constraint6, Constraint7, Constraint8, Constraint9, Constraint10];

欢迎感兴趣的小伙伴关注，小编会不定期更新高质量的学习资料、文章和程序代码，为您的科研加油助力！