概率图模型是一种用图形表示概率分布和条件依赖关系的数学模型。概率图模型可以分为两大类：有向图模型和无向图模型。有向图模型也叫贝叶斯网络，它用有向无环图表示变量之间的因果关系。无向图模型也叫马尔可夫网络，它用无向图表示变量之间的相关关系。概率图模型可以用于机器学习，人工智能，自然语言处理，计算机视觉，生物信息学等领域。

一、马尔科夫模型

随机过程

马尔科夫过程

马尔科夫链

状态转移矩阵通过训练样本学习得到，采用最大似然估计

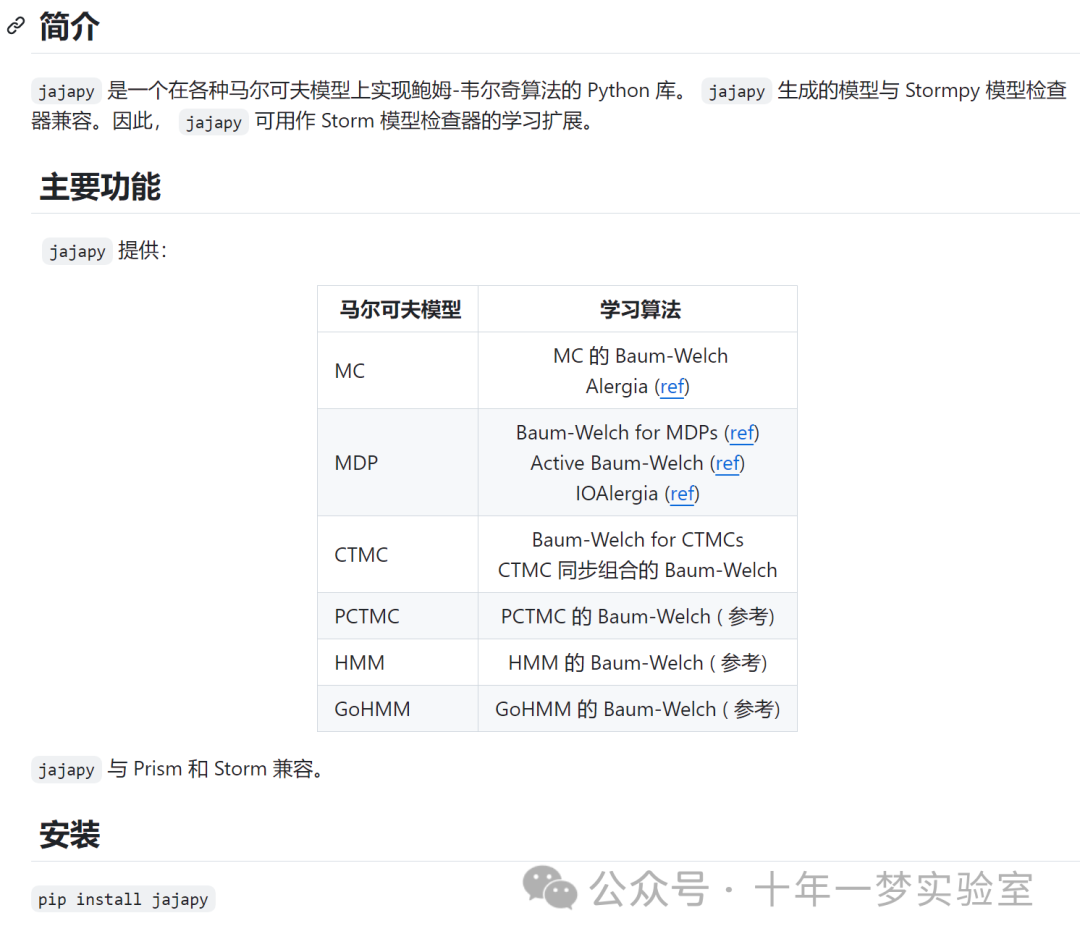
二、隐马尔可夫模型简介

2.1 模型结构

隐马尔可夫模型（Hidden Markov Model，HMM）

隐马尔可夫模型（Hidden Markov Model，HMM）是一种统计模型，用于描述一个含有隐含未知参数的马尔可夫过程。在隐马尔可夫模型中，隐藏状态（Hidden State）和观测值（Observation）的数量是根据实际问题人工设定的，例如，如果我们用隐马尔可夫模型来进行中文分词，那么隐藏状态的数量可以设为4，分别表示词语的开始（B）、中间（M）、结束（E）和单字词（S），观测值的数量可以设为汉字的种类数。状态转移矩阵（Transition Matrix）和混淆矩阵（Confusion Matrix）是隐马尔可夫模型的两个重要参数，分别描述了隐藏状态之间的转移概率和隐藏状态与观测值之间的发射概率。这两个参数可以通过样本学习得到，例如，可以使用最大似然估计或贝叶斯估计的方法，根据给定的状态序列和观测序列，估计这两个参数的值。

隐马尔可夫模型需要解决以下三个基本问题：

• 概率计算问题：给定模型参数和观测序列，计算该观测序列出现的概率。这个问题可以使用前向算法（Forward Algorithm）或后向算法（Backward Algorithm）来求解，它们都是基于动态规划（Dynamic Programming）的方法，可以有效地利用中间结果，避免重复计算，提高效率。

• 学习问题：给定观测序列，估计模型参数。这个问题可以使用鲍姆-韦尔奇算法（Baum-Welch Algorithm）或期望最大化算法（Expectation-Maximization Algorithm）来求解，它们都是基于迭代（Iteration）的方法，可以从一个初始的参数值开始，不断地更新参数，直到收敛到一个局部最优解。

• 预测问题：给定模型参数和观测序列，求最有可能的隐藏状态序列。这个问题可以使用维特比算法（Viterbi Algorithm）来求解，它也是基于动态规划的方法，可以找到一条最优的状态路径，使得该路径下的观测序列的概率最大。

2.2 中文分词

三、估值问题

四、解码问题

五、训练算法

六、应用

示例代码：

• 该代码是一个用 jajapy 库实现的隐马尔可夫模型（HMM）的例子，用于生成和学习观测序列。

• 该代码首先创建了一个 HMM，指定了状态转移矩阵、发射矩阵和初始状态概率，然后用该模型生成了一个训练集，包含 1000 个长度为 10 的观测序列。

• 该代码接着创建了一个随机的初始假设模型，然后用鲍姆-韦尔奇算法（BW）对其进行训练，得到一个输出模型，该模型尽可能地拟合训练集。

• 该代码最后用原始模型和输出模型分别生成了一个测试集，包含 1000 个长度为 10 的观测序列，然后计算了两个模型在测试集上的对数似然，并用对数似然之差作为评估指标，输出到屏幕上。

import jajapy as ja # 导入 jajapy 库，这是一个用于创建和训练隐马尔可夫模型的库def example_7():# 模型创建#----------------# 在下一个状态 (s0) 中，我们以 0.4 的概率生成 'x'，以 0.6 的概率生成 'y'# 一旦生成了一个观测值，我们就以 0.5 的概率转移到状态 1 或 2transitions = [(0,1,0.5),(0,2,0.5),(1,3,1.0),(2,4,1.0),(3,0,0.8),(3,1,0.1),(3,2,0.1),(4,3,1.0)] # 定义转移矩阵，每个元素表示从一个状态到另一个状态的概率emission = [(0,"x",0.4),(0,"y",0.6),(1,"a",0.8),(1,"b",0.2),(2,"a",0.1),(2,"b",0.9),(3,"x",0.5),(3,"y",0.5),(4,"y",1.0)] # 定义发射矩阵，每个元素表示在一个状态下生成一个观测值的概率original_model = ja.createHMM(transitions,emission,initial_state=0,name="My HMM") # 使用转移矩阵和发射矩阵创建一个隐马尔可夫模型，初始状态为 0，模型名称为 "My HMM"#original_model.save("my_model.txt") # 将模型保存到文件中#original_model = ja.loadHMM("my_model.txt") # 从文件中加载模型# 训练集生成#------------------------# 我们生成 1000 个长度为 10 的观测序列training_set = original_model.generateSet(set_size=1000, param=10) # 使用模型生成训练集，参数 set_size 表示训练集的大小，param 表示每个序列的长度#training_set.save("my_training_set.txt") # 将训练集保存到文件中#training_set = ja.loadSet("my_training_set.txt") # 从文件中加载训练集# 学习#---------initial_hypothesis = ja.HMM_random(5,alphabet=list("abxy"),random_initial_state=False) # 创建一个随机的假设模型，参数 5 表示状态的数量，alphabet 表示观测值的集合，random_initial_state 表示是否随机选择初始状态output_model = ja.BW().fit(training_set, initial_hypothesis) # 使用鲍姆-韦尔奇算法（BW）对假设模型进行训练，参数 training_set 表示训练集，initial_hypothesis 表示初始假设，返回一个训练后的模型# 输出评估#------------------# 我们生成 1000 个长度为 10 的观测序列test_set = original_model.generateSet(set_size=1000, param=10) # 使用原始模型生成测试集，参数 set_size 表示测试集的大小，param 表示每个序列的长度ll_original = original_model.logLikelihood(test_set) # 计算原始模型在测试集上的对数似然ll_output   =   output_model.logLikelihood(test_set) # 计算训练后的模型在测试集上的对数似然quality = abs(ll_original - ll_output) # 计算两个模型的对数似然之差，作为评估指标print("loglikelihood distance:",quality) # 打印评估指标if __name__ == "__main__":example_7() # 调用 example_7 函数

输出：

/07-hmm.py

WARNING: Stormpy not found.

Learning an HMM...

WARNING: stormpy not found. The output model will be a Jajapy model

|████████████████████████████████████████| 104 in 3:22.9 (0.51/s)

loglikelihood distance: 0.4953666912796937