谷禾健康

生态学家在分析微生物组和感兴趣的协变量(如临床结果或环境因素)之间的关联时，经常以两种方式查看物种分类计数数据。

一种是将计数视为定量的(即作为相对丰度数据进行分析)；另一种是将计数数据离散化，只表明一个分类单元在样本中是否存在。

虽然第一种方法在医学文献中可能更常见，但这种关联也可能是由于样本中存在或不存在的分类群的变化所驱动的。例如，在人类肠道中，物种丰富度的增加与更稳定的生态系统有关，生态系统往往对饮食、抗生素使用和病原体入侵等环境压力更具有抵抗力。

相比之下，健康的阴道微生物群的特点往往是以Lactobacilli为主的低多样性。研究人员认为当常见的分类群占主导地位时，基于相对丰度的分析可能更合理，而当稀有分类群占主导地位时，基于存在或不存在的分析可能表现更好。

目前最常用的分析方法是基于未加权的UniFrac和Jaccard距离的PERMANOVA统计检验，但是它只给出了整个群落的关联，没有给出与单个分类群的关联。Fisher’s精确检验可以检验协变量与单个分类群是否存在关联，对于更复杂的情况，可以使用精确的逻辑回归，但计算成本较高。

LDM本身是一种线性模型，研究人员对它进行了扩展，使得该方法可以基于稀疏计数数据，来分析协变量与群落或单个分类群之间的关联，同时控制混杂协变量（例如实验中出现的提取和扩增偏差），协变量可以是离散的也可以是连续的。

方法

在LDM中，元数据被放入矩阵X中(行对应N个样本，列对应协变量)。将X的列分为K组，这里可以理解为”子模型“，每个子模型代表一组想要联合检验的变量。

LDM使X的列正交。设Y为N×J（原始）分类群计数表，共有J个分类群。

Hk为子模型的帽子矩阵

H0为完整模型X的帽子矩阵

↘
计算帽子矩阵得到模型预测值

通过计算完整模型的帽子矩阵可以得到在整个模型下的预测值。帽子矩阵可以用来计算残差，即实际观测值与模型预测值之间的差异。

同时，帽子矩阵也可以用来评估模型的拟合优度，例如通过计算决定系数（R-squared）来衡量模型对数据的解释程度。

研究人员表示由于LDM使用排列法评估显著性，在计算中没有考虑通常涉及自由度的乘法因子，并对通常的F-statisc加1。因此，LDM的检验统计量是在排除子模型k的模型中计算的残差平方和（RSS）与包含子模型k的模型中计算的RSS之比。

Fkj指所有分类群上特定于分类群的检验统计量的比值之和。总而言之，LDM使用残差来衡量子模型的效应，然后计算F-statisc来判断子模型是否对分类群产生显著影响，计算公式：

↘
如何使用LDM结合稀疏的数据

其中B的元素根据Y是否大于0来确定，I是指示函数。然后使用上面的公式，将矩阵Y替换为矩阵B，计算F-statisc。

最后作者给出来两种方式来结合稀疏的数据，选择取平均值或比值，并通过对协变量进行排列来进行分类群水平和整个群落的检验。但是作者也表示选择平均值较为稳妥。

使用模拟数据集测试LDM

模拟数据由50个病例和50个对照构成，根据上呼吸道微生物组（URT）的856个物种的相对丰度进行了模拟。

为了模拟在病例中存在而在对照中不存在的物种，从中均匀的选择了100个物种，并与病例-对照状态相关联。同时，单独选择了另外100个物种与混杂因子相关联，这是一个二元变量，在对照组与病例组中的分布为7:3。其中与病例-对照状态、混杂因子相关联的物种可能会有重叠。

↘
不同LDM使用方式的性能

在模拟数据集中，作者比较了不同LDM使用方式的性能。

LDM-A作为基准，也是本篇文章的中心—一种扩展的LDM方法，它代表对所有稀释后的数据计算残差平方和（RSS）的平均值。

LDM-F(R)，指通过对R次稀释后的数据计算平均F-statisc，这里的R在文中等于1或5。

LDM-UR，指对未稀释的矩阵（方法中的矩阵B）进行分析。

LDM-L，指在未稀释的数据中将库大小调整为一个协变量，并在LDM中应用。比较的结果基于10000次模拟重复实验。显著性水平定义为0.05。

结果如上图所示，LDM-UR的性能随着病例和对照之间的文库大小差异增加而变差，而其他方法都可以控制文库大小差异带来的影响。其中LDM-L的成功可能是因为文库大小本质上是一个二元变量，如果不是这个数据类型，LDM-L在更复杂的情况下可能表现不佳。

接着作者将平均文库大小统一固定为10k、5k和1.5k、1k，在此基础上比较LDM-A、LDM-F(5)和LDM-L的性能。

结果如下图所示，纵坐标为Power的图表示在整个群落中的表现能力，其中LDM-A表现最出色。

文中的Power指的是统计功效（statistical power）值，指在进行假设检验时，能够正确拒绝一个错误的零假设的概率。

纵坐标为sensitivity的图表示在分类群中，检验差异存在的敏感性，其中LDM-A具有最高的敏感性，相比之下，LDM-F(5)和LDM-L较低。

纵坐标为empirical FDR表示假阳性发现率，所有方法都在可接受范围内（＜10%）。

编辑​

虽然LDM-UR方法在控制文库大小差异影响表现最差，但作者发现LDM-UR对未稀释的数据进行分析是有效的，并且可以期望达它达到最佳的功效，因为它使用了全部reads。

★ 使用适当的稀释深度，功效损失将很小

于是作者将LDM-A和LDM-UR进行了比较，给定两个稀释深度水平，即均值库大小的25%和10%（稀释深度也是数据中生成的最小库大小），观察当没有文库大小这类系统差异时，这两种LDM方法在不同稀释比例数据中的表现。

结果如下图所示，与分析完整数据的相比，稀释确实会导致功效损失，但随着均值库大小的增加，功效损失逐渐减小。

在较高的稀释深度下，当均值库大小超过一定阈值时，LDM-A的功效与LDM-UR相当。因此，考虑到现代测序技术产生的大型文库的大小，只要使用适当的稀释深度，预计功效损失将很小。

使用IBD数据集测试LDM

对来自RISK队列的数据子集进行了分析，该队列研究了新发炎性肠病(IBD)的儿童患者以及非IBD对照组。

作者选择了该数据子集中的来自直肠黏膜组织活检的数据。过滤掉了文库大小＜10000的样本，相当于丢失了10%的样本。此外还过滤掉了在少于5个样本中存在的分类群。

最终留下267个样本的2565个分类群，共169个病例和98个对照。由于数据中男性比例存在不平衡（病例组为62%，对照组为44%），作者便将性别和抗生素使用作为需要控制的混杂因子，使用LDM检验直肠微生物组与IBD状态的存在-缺失关联。重点关注在群落水平上进行的关联分析，并检测对群落水平关联有显著贡献的个别分类群。

↘
病例和对照组的文库大小分布

首先调查了所选数据中病例和对照组的文库大小分布，结果如下图所示，发现文库大小分布确实存在系统差异（同模拟数据）。因此对所有样本的读取计数数据进行了稀释，将测序深度稀释到最小值10081。

作者在文中提到在补充数据中，对去除性别和抗生素使用影响后的数据利用Jaccard距离绘制排序图，分别进行了无稀释和一次稀释的分析。

结果显示病例组与对照组在稀释前后都有明显的差异。且在没有稀释的情况下，两组差异更明显，这证实了文库大小的混杂效应。

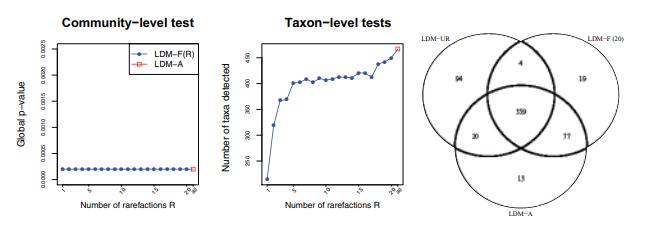
接着作者对数据集应用LDM-A和LDM-F(R)方法，其中稀释次数R在1到20之间变化。分析结果如下图。

最左的图展示了在群落水平上，直肠微生物组与炎症性肠病状态存在-缺失关联分析的P值，这些P值表明，在群落水平上，炎症性肠病状态与直肠微生物组之间存在非常强的存在-缺失关联。

中间的图展示了在FDR为10%时，在病例和对照之间检测到差异的分类群数量，数据表明随着稀释次数从1增加到5，LDMF(R)检测到的分类群数量急剧增加，并在5次稀释后趋于稳定，这进一步证实数据至少需要进行5次稀释。

最右的韦恩图展示了LDM-UR、LDM-F(20)和LDM-A检测到的唯一或共同存在的分类群数目，数据显示，LDM-F(20)和LDM-A检测到的分类群集合有很大的重叠，而LDM-UR检测到的分类群集合中有很多（94个）与其他任何集合都不重叠，作者认为这些可能是由于文库大小混杂导致的假阳性结果。

编辑​

结论

作者在文中提出了两种有效的LDM扩展方法，LDM-A和LDM-F(R)，它们分别使用不同的F-statisc计算方法。

LDM-A将分子和分母的残差平方和分别进行平均，取比值。而LDM-F(R)则对R次稀释重复的F-statisc进行平均。

根据测试结果，作者建议使用LDM-A而不是LDM-F(R)，因为它有以下优点：(i) 不需要选择稀释重复次数；(ii) 在功效以及对于检测个别分类群的敏感性方面比LDM-F(R)更强；(iii) 计算效率更高。

注：作者已将该方法构建为R包，可使用’devtools::install_github("yijuanhu/LDM", build_vignettes=TRUE)’安装。

// Tips

在比这篇文章迟些发表的”A comprehensive evaluation of microbial differential abundance analysis methods: current status and potential solutions.”文章中提到，LDM方法虽然在统计方面有最好的功效，但在强成分效应存在的情况下，其对假阳性控制并不好。

该文章对多种差异分析方法做了比较评估。虽然它引用的文章是”Testing hypotheses about the microbiome using the linear decomposition model (LDM).”，这时的LDM方法还未进行上述的扩展。但我们仍然推荐阅读，以提供不同的视角。

参考文献：

Hu YJ, Lane A, Satten GA. A rarefaction-based extension of the LDM for testing presence-absence associations in the microbiome. Bioinformatics. 2021 Jul 19;37(12):1652-1657.