day13 滑动窗口最大值前K个高频元素

题目1：239 滑动窗口最大值

题目链接：239 滑动窗口最大值

题意

长度为K的滑动窗口从整数数组的最左侧移动到最右侧，每次只移动1位，求滑动窗口中的最大值

不能使用优先级队列，如果使用大顶堆，最终要pop的元素不知道是哪一个，因为大顶堆已经对队列中的元素进行排序了，元素的顺序发生了改变

暴力解法

对窗口内的所有元素进行排序

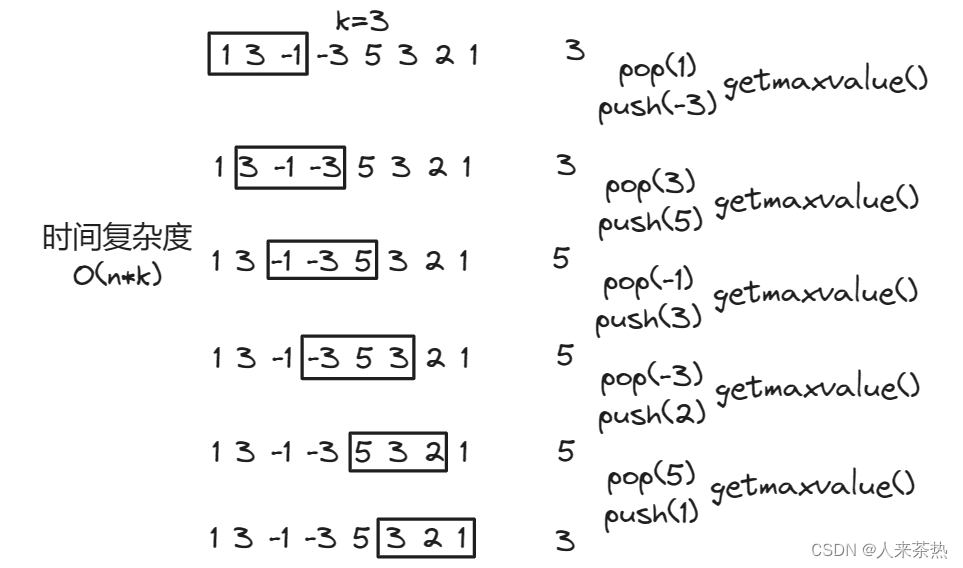
单调队列

由于窗口每次只移动1步，所以每真正push一次，就收集一次最大值即可，最大值放到队列的出口

队列只维护窗口中的最大值即可，且队列里的元素是从左到右依次递减的

pop()：若滑动窗口原本要移除的元素(val)就是单调队列的出口(front)元素(滑动窗口的最大值)，那么就弹出元素

push()：如果要放入的元素(val)大于入口(back)的元素，就将入口处(back)小于val的元素逐个卷走，元素再在入口处(back)处入栈

getmaxvalue()：每次移动窗口时，队列出口处(front())的元素即为当前窗口的最大值

伪代码

逻辑

例1：前一个滑动窗口删除的元素会不会影响后一个滑动窗口？

代码

class Solution {  
private:class MyQueue{public:deque<int> que;//双向队列void pop(int val){if(!que.empty()&&que.front()==val){que.pop_front();}}void push(int val){//去掉入口处比其小的元素while(!que.empty()&&que.back()<val){que.pop_back();}que.push_back(val);}int getmaxvalue(){return que.front();}};    
public:vector<int> maxSlidingWindow(vector<int>& nums, int k) {MyQueue que;vector<int> result;for(int i=0;i<k;i++){que.push(nums[i]);}//第一个滑动窗口的元素result.push_back(que.getmaxvalue());for(int i=k;i<nums.size();i++){//先弹出元素，因为窗口的大小是一定的，只能先弹出元素，再放入元素que.pop(nums[i-k]);//再放入元素que.push(nums[i]);//求最大值result.push_back(que.getmaxvalue());}return result;}
};

时间复杂度: O(n)
空间复杂度: O(k)

题目2：347 前K个高频元素

题目链接：347 前K个高频元素

题意

返回整数数组nums中出现频率前k高的元素

暴力解法

使用map数组，元素是key，频率是value，然后将value从大到小排序，输出前k个元素（所有元素进行排序）

优先级队列(小顶堆)

为了优化时间复杂度，可以只维护k个元素，没有必要排序所有元素，想到使用优先级队列。

大顶堆，小顶堆擅长求解在大数据集内求排名靠前的元素，堆的底层实现是二叉树

那么使用大顶堆还是使用小顶堆呢？

如果使用大顶堆，那么加入该元素时，弹出最大值，不符题意

如果使用小顶堆，那么加入该元素时，弹出最小值，符合题意，所以，使用小顶堆

使用优先级队列实现大顶堆的话，cmopare函数从大到小排，实现小顶堆的话，compare函数从小到大排

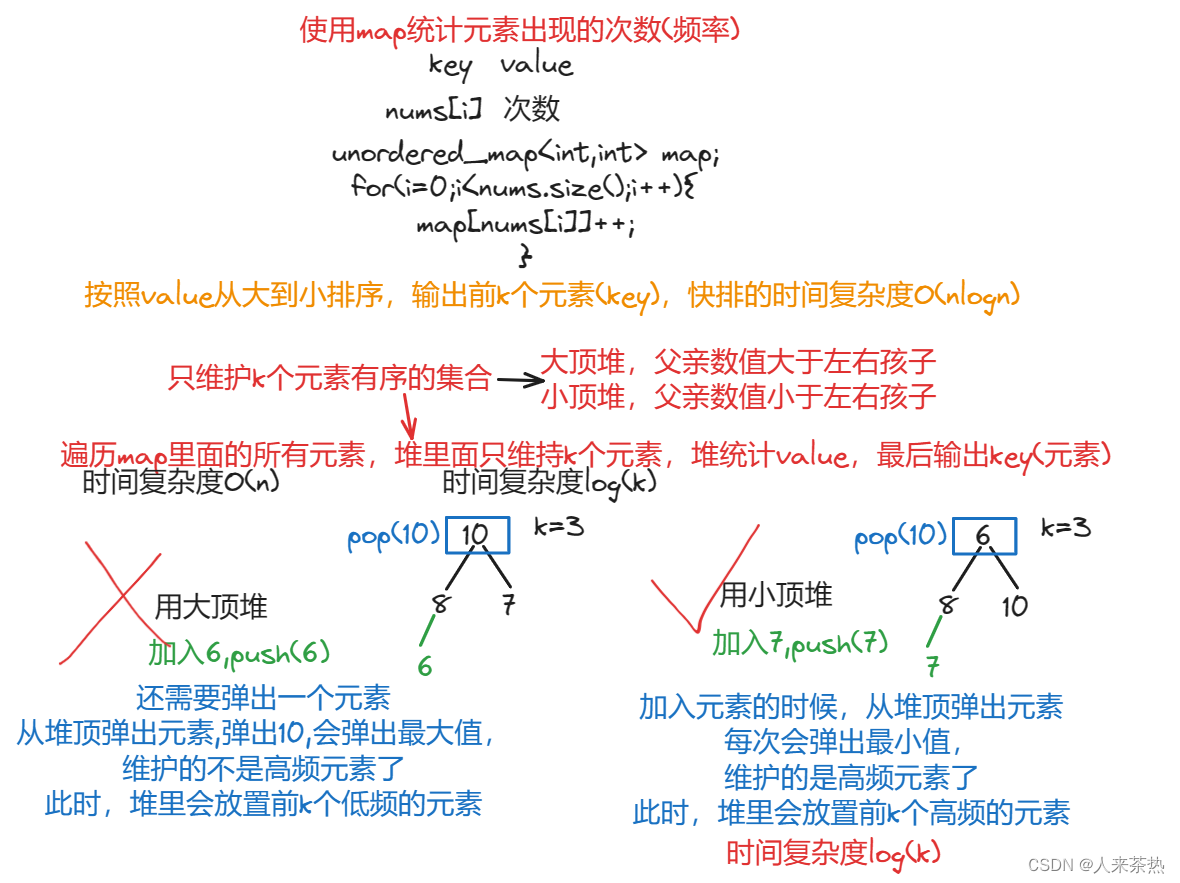
伪代码

代码

class Solution {
public:class mycomparision{public:bool operator()(const pair<int,int>& kv1,const pair<int,int>& kv2){return kv1.second > kv2.second;}};//定义一个类之后，一定要添加;vector<int> topKFrequent(vector<int>& nums, int k) {unordered_map<int,int> map;//统计元素出现的频率for(int i=0;i<nums.size();i++){map[nums[i]]++;}//使用优先级队列定义小顶堆priority_queue<pair<int,int>,vector<pair<int,int>>,mycomparision> que;//pair<int,int>表示键值对的数据类型<元素(int),频率(int)>//vector<pair<int,int>>表示vector作为que的底层容器，存储元素//遍历map中的元素，小顶堆只维护前k个高频元素for(unordered_map<int,int>::iterator it=map.begin();it!=map.end();it++){que.push(*it);//*it代表迭代器it指向的key-value键值对if(que.size()>k){que.pop();//弹出当前小顶堆中的最小值}}//将小顶堆中频率排名前k的key元素按照频率从高到低放到数组中vector<int> result(k);//这里一定要定义result的大小，因为后续是对result的下标位置进行操作for(int i=k-1;i>=0;i--){result[i] = que.top().first;que.pop();}return result;}
};

时间复杂度: O(nlogk)
空间复杂度: O(n)