文章目录
- 前言
- 1. 排序算法的复杂度及稳定性分析
- 2. 排序算法的性能测试
- 2.1 重复率较低的随机值排序测试
- 2.2 重复率较高的随机值排序测试
前言
本篇是基于我这几篇博客做的一个总结:
- 《简单排序》(含:冒泡排序,直接插入排序,选择排序,计数排序)
- 《希尔排序》
- 《堆排序》
- 《快速排序》
- 《归并排序》
我会再对他们的时间复杂度、空间复杂度以及稳定性再做一次总结,并且在不同的场景下,测试他们的性能怎么样。
1. 排序算法的复杂度及稳定性分析
| 排序方法 | 平均情况 | 最好情况 | 最坏情况 | 辅助空间 | 稳定性 |
|---|---|---|---|---|---|
| 冒泡排序 | O O O( N N N2) | O O O( N N N) | O O O( N N N2) | O O O( 1 1 1) | 稳定 |
| 选择排序 | O O O( N N N2) | O O O( N N N2) | O O O( N N N2) | O O O( 1 1 1) | 不稳定 |
| 直接插入排序 | O O O( N N N2) | O O O( N N N) | O O O( N N N2) | O O O( 1 1 1) | 稳定 |
| 计数排序 | O O O( N + r a n g e N+range N+range) | O O O( N N N) | O O O( N + r a n g e N+range N+range) | O O O( r a n g e range range) | — |
| 希尔排序 | O O O( N ∗ l o g N N*logN N∗logN) ~ O O O( N N N2) | O O O( N N N1.3) | O O O( N N N2) | O O O( 1 1 1) | 不稳定 |
| 堆排序 | O O O( N ∗ l o g N N*logN N∗logN) | O O O( N ∗ l o g N N*logN N∗logN) | O O O( N ∗ l o g N N*logN N∗logN) | O O O( 1 1 1) | 不稳定 |
| 归并排序 | O O O( N ∗ l o g N N*logN N∗logN) | O O O( N ∗ l o g N N*logN N∗logN) | O O O( N ∗ l o g N N*logN N∗logN) | O O O( N N N) | 稳定 |
| 快速排序 | O O O( N ∗ l o g N N*logN N∗logN) | O O O( N ∗ l o g N N*logN N∗logN) | O O O( N N N2) | O O O( l o g N logN logN) ~ O O O( N N N) | 不稳定 |
2. 排序算法的性能测试
⚠️:我这里只是测试一遍的结果截图,目的是让大家看看,判断一个排序的优劣需要不同场景下的大量测试。
我们比较排序时,应该换成release版本来测试,这样性能才会全部拉满
先写一段测试代码
// 测试排序的性能对比
// 测试排序的性能对比
void TestOP()
{srand(time(0));const int N = 100000; // 十万个数的比较int* a1 = (int*)malloc(sizeof(int) * N);int* a2 = (int*)malloc(sizeof(int) * N);int* a3 = (int*)malloc(sizeof(int) * N);int* a4 = (int*)malloc(sizeof(int) * N);int* a5 = (int*)malloc(sizeof(int) * N);int* a6 = (int*)malloc(sizeof(int) * N);int* a7 = (int*)malloc(sizeof(int) * N);int* a8 = (int*)malloc(sizeof(int) * N);for (int i = 0; i < N; ++i){a1[i] = rand() + i; // 生成十万个重复率低的随机值//a1[i] = rand() % 100; // 生成十万个重复率高的随机值a2[i] = a1[i];a3[i] = a1[i];a4[i] = a1[i];a5[i] = a1[i];a6[i] = a1[i];a7[i] = a1[i];a8[i] = a1[i];}int begin1 = clock();InsertSort(a1, N);int end1 = clock();int begin2 = clock();SelectSort(a2, N);int end2 = clock();int begin3 = clock();ShellSort(a3, N);int end3 = clock();int begin4 = clock();HeapSort(a4, N);int end4 = clock();int begin5 = clock();QuickSort(a5, 0, N);int end5 = clock();int begin6 = clock();MergeSort(a6, N);int end6 = clock();int begin7 = clock();QuickSortNonR(a7, 0, N);int end7 = clock();int begin8 = clock();MergeSortNonR(a8, N);int end8 = clock();printf("InsertSort:%d\n", end1 - begin1);printf("SelectSort:%d\n", end2 - begin2);printf("ShellSort:%d\n", end3 - begin3);printf("HeapSort:%d\n", end4 - begin4);printf("QuickSort:%d\n", end5 - begin5);printf("MergeSort:%d\n", end6 - begin6);printf("QuickSortNonR:%d\n", end7 - begin7);printf("MergeSortNonR:%d\n", end8 - begin8);free(a1);free(a2);free(a3);free(a4);free(a5);free(a6);
}int main()
{srand((unsigned)time(NULL)); // 生成随机数种子TestOP();return 0;
}
2.1 重复率较低的随机值排序测试
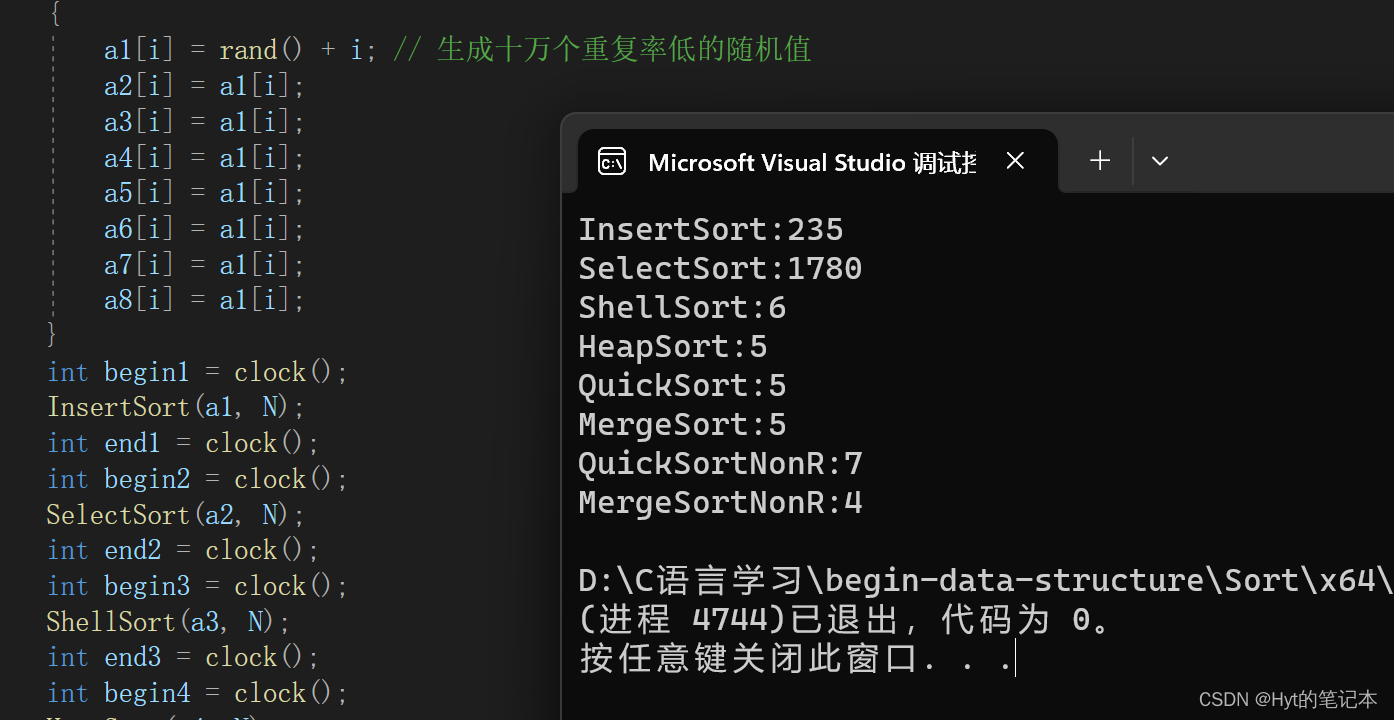
可以看到,直接插入排序在比较低阶的排序算法中,算是很优秀的一个排序了。
我们继续加大数据,但是我得把效率比较低的排序关掉,单独来比那些比较高阶的排序:
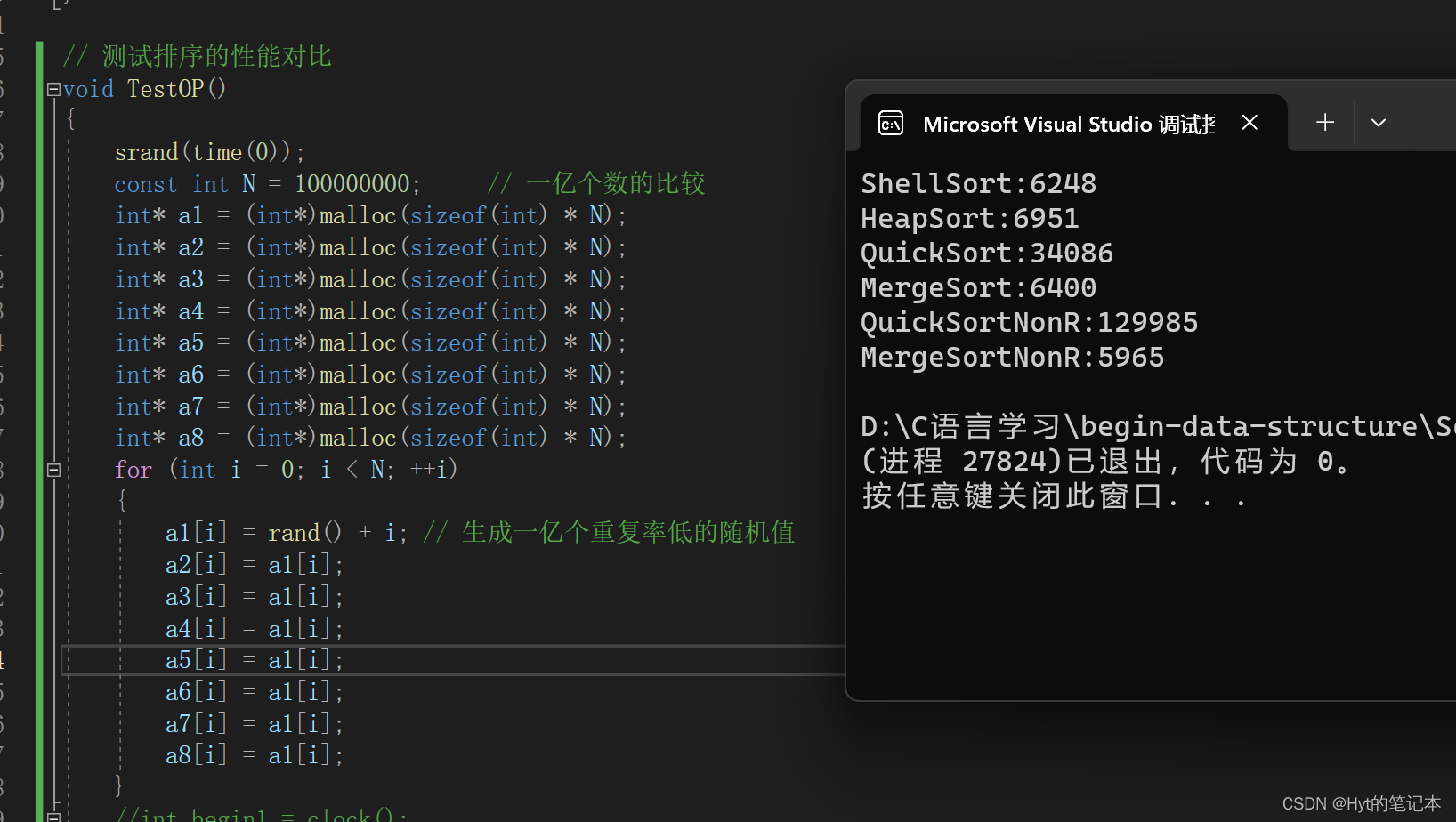
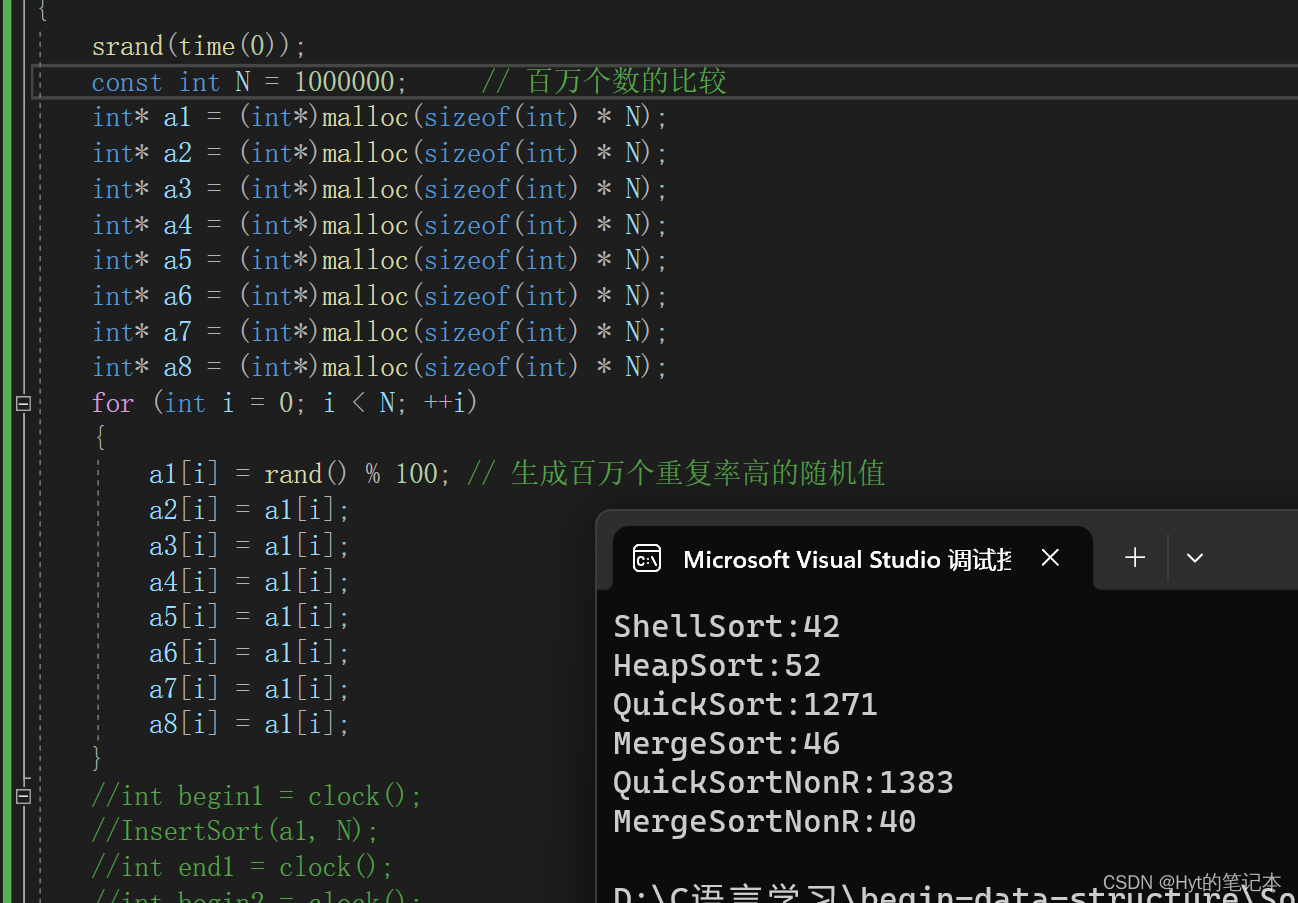
2.2 重复率较高的随机值排序测试
直接看结果:
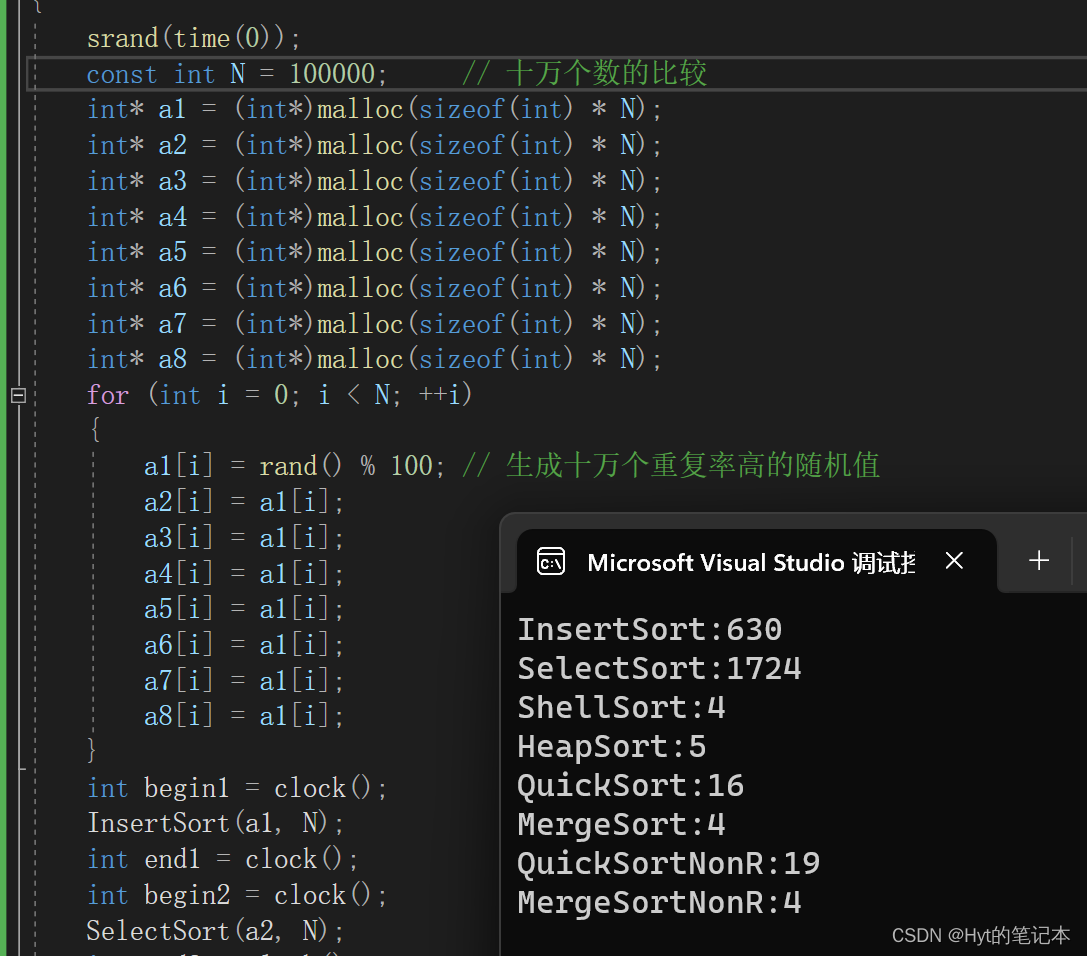
继续加大数据,把效率比较低的排序关掉,单独来比那些比较高阶的排序:
消息的持久化)
?)




,成为Linq高手!)







)




