一、题目

给你一个n * n矩阵grid，矩阵由若干0和1组成。请你用四叉树表示该矩阵grid。你需要返回能表示矩阵grid的四叉树的根结点。四叉树数据结构中，每个内部节点只有四个子节点。此外，每个节点都有两个属性：
【1】val：储存叶子结点所代表的区域的值。1对应True，0对应False。注意，当isLeaf为False时，你可以把True或者False赋值给节点，两种值都会被判题机制接受。
【2】isLeaf: 当这个节点是一个叶子结点时为True，如果它有4个子节点则为False。

class Node {public boolean val;public boolean isLeaf;public Node topLeft;public Node topRight;public Node bottomLeft;public Node bottomRight;
}

我们可以按以下步骤为二维区域构建四叉树：
【1】如果当前网格的值相同（即，全为0或者全为1），将isLeaf设为True，将val设为网格相应的值，并将四个子节点都设为Null然后停止。
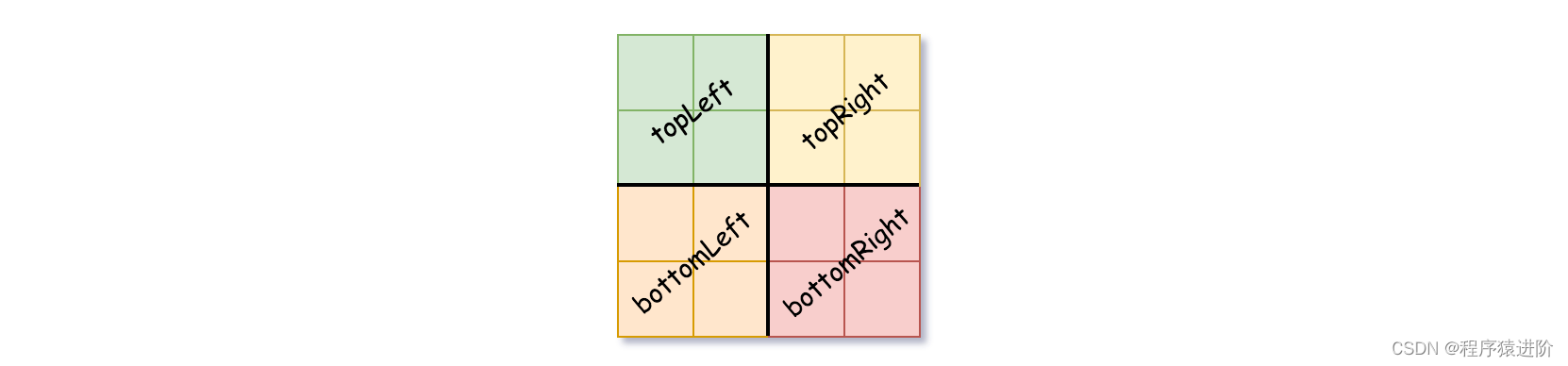
【2】如果当前网格的值不同，将isLeaf设为False，将val设为任意值，然后如下图所示，将当前网格划分为四个子网格。
【3】使用适当的子网格递归每个子节点。

四叉树格式： 你不需要阅读本节来解决这个问题。只有当你想了解输出格式时才会这样做。输出为使用层序遍历后四叉树的序列化形式，其中null表示路径终止符，其下面不存在节点。它与二叉树的序列化非常相似。唯一的区别是节点以列表形式表示[isLeaf, val]。如果isLeaf或者val的值为True，则表示它在列表[isLeaf, val]中的值为1；如果isLeaf或者val的值为False，则表示值为0。

示例 1：

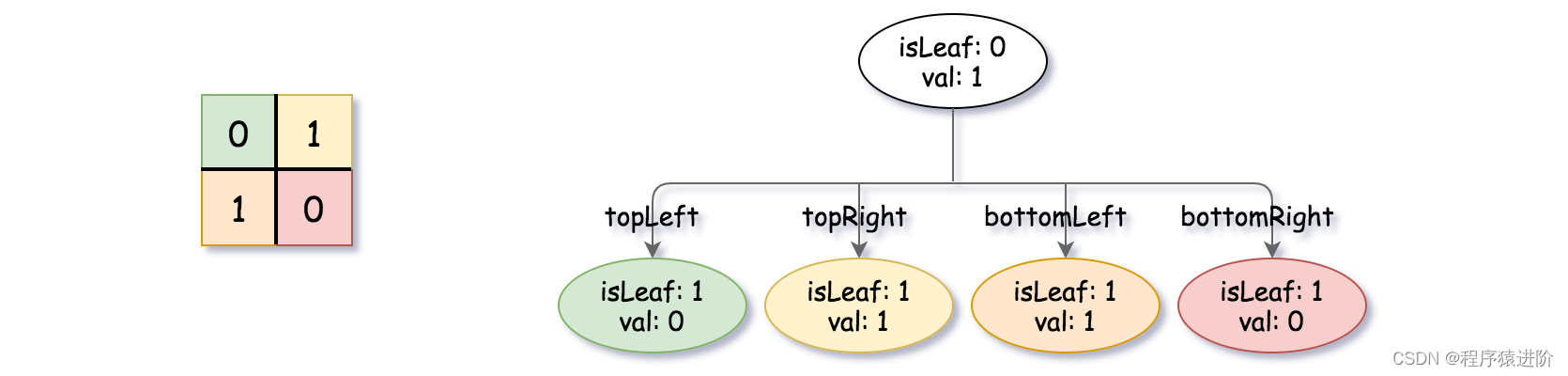
输入：grid = [[0,1],[1,0]]
输出：[[0,1],[1,0],[1,1],[1,1],[1,0]]
解释：此示例的解释如下：请注意，在下面四叉树的图示中，0表示false，1表示True。

示例 2：

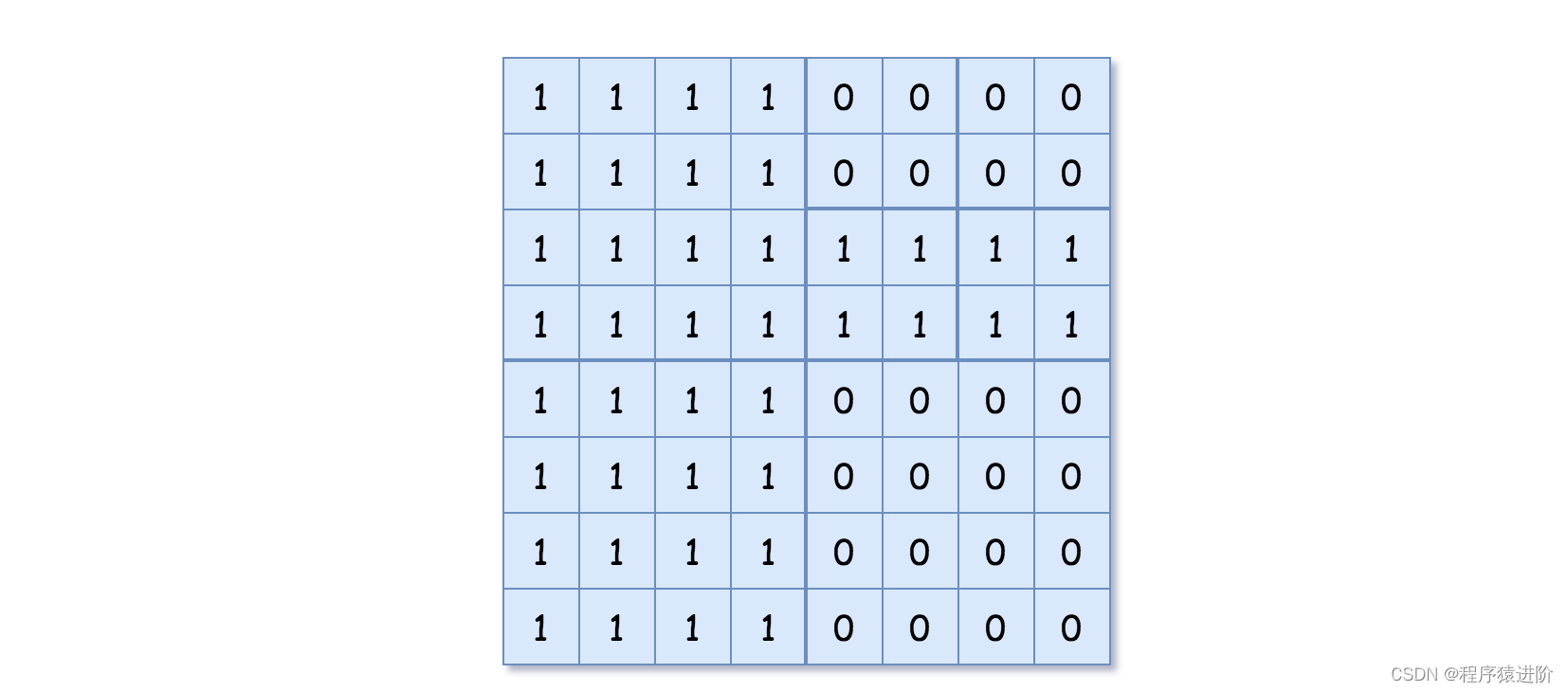
输入：grid = [[1,1,1,1,0,0,0,0],[1,1,1,1,0,0,0,0],[1,1,1,1,1,1,1,1],[1,1,1,1,1,1,1,1],[1,1,1,1,0,0,0,0],[1,1,1,1,0,0,0,0],[1,1,1,1,0,0,0,0],[1,1,1,1,0,0,0,0]]
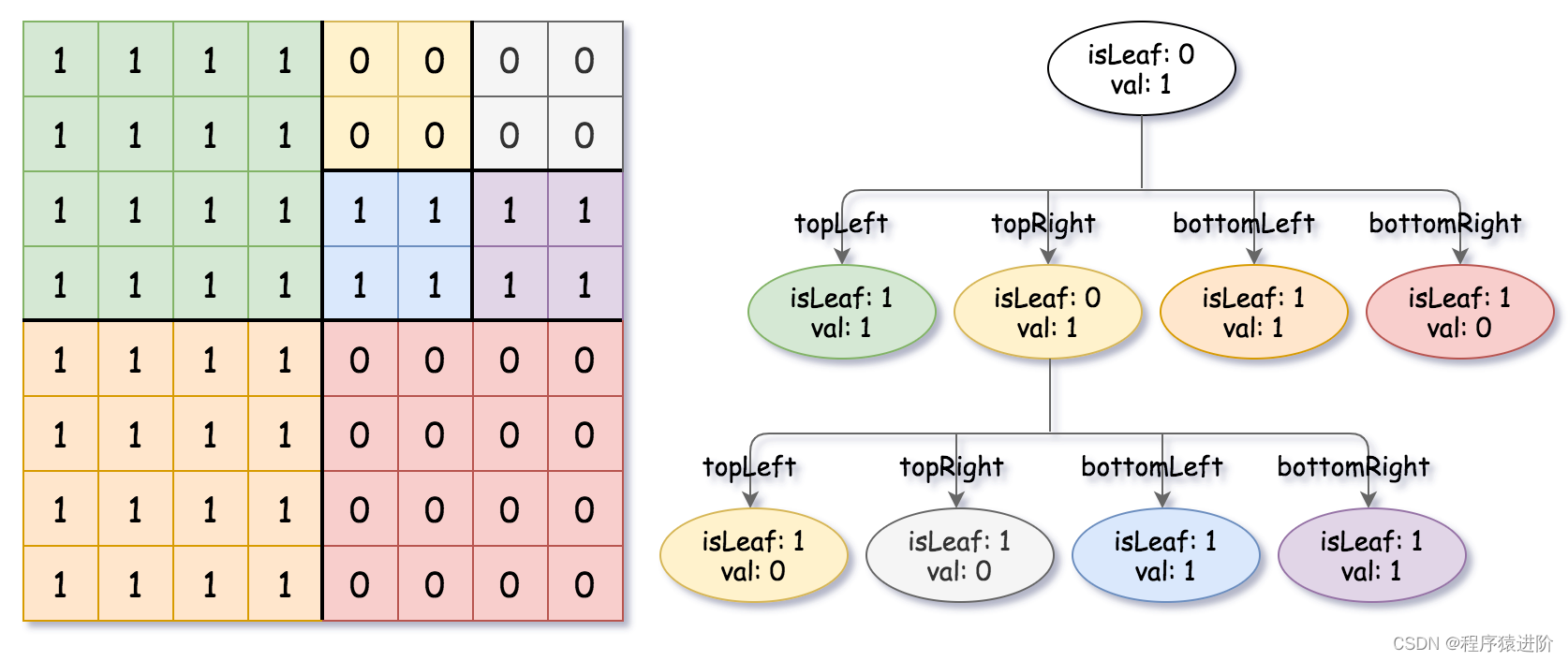
输出：[[0,1],[1,1],[0,1],[1,1],[1,0],null,null,null,null,[1,0],[1,0],[1,1],[1,1]]
解释：网格中的所有值都不相同。我们将网格划分为四个子网格。topLeft，bottomLeft和bottomRight均具有相同的值。topRight具有不同的值，因此我们将其再分为4个子网格，这样每个子网格都具有相同的值。解释如下图所示：

n == grid.length == grid[i].length
n == 2x其中0 <= x <= 6

二、代码

【1】递归： 我们可以使用递归的方法构建出四叉树。具体地，我们用递归函数dfs(r0,c0,r1,c1)处理给定的矩阵grid从r0行开始到r1−1行，从c0和c1−1列的部分。我们首先判定这一部分是否均为0或1，如果是，那么这一部分对应的是一个叶节点，我们构造出对应的叶节点并结束递归；如果不是，那么这一部分对应的是一个非叶节点，我们需要将其分成四个部分：行的分界线为(r0+r1)/2​​，列的分界线为(c0+c1)/2​​，根据这两条分界线递归地调用dfs函数得到四个部分对应的树，再将它们对应地挂在非叶节点的四个子节点上。

class Solution {public Node construct(int[][] grid) {return dfs(grid, 0, 0, grid.length, grid.length);}public Node dfs(int[][] grid, int r0, int c0, int r1, int c1) {boolean same = true;for (int i = r0; i < r1; ++i) {for (int j = c0; j < c1; ++j) {if (grid[i][j] != grid[r0][c0]) {same = false;break;}}if (!same) {break;}}if (same) {return new Node(grid[r0][c0] == 1, true);}Node ret = new Node(true,false,dfs(grid, r0, c0, (r0 + r1) / 2, (c0 + c1) / 2),dfs(grid, r0, (c0 + c1) / 2, (r0 + r1) / 2, c1),dfs(grid, (r0 + r1) / 2, c0, r1, (c0 + c1) / 2),dfs(grid, (r0 + r1) / 2, (c0 + c1) / 2, r1, c1));return ret;}
}

时间复杂度： O(n^2log⁡n)。这里给出一个较为宽松的时间复杂度上界。记T(n)为边长为n的数组需要的时间复杂度，那么「判定这一部分是否均为0或1」需要的时间为O(n^2)，在这之后会递归调用4规模为n/2的子问题，那么有：T(n)=4T(n/2)+O(n^2)以及：T(1)=O(1)根据主定理，可以得到T(n)=O(n^2log⁡n)。但如果判定需要的时间达到了渐近紧界Θ(n^2)，那么说明这一部分包含的元素大部分都是相同的，也就是说，有很大概率在深入递归时遇到元素完全相同的一部分，从而提前结束递归。因此O(n^2log⁡n)的时间复杂度是很宽松的，实际运行过程中可以跑出与方法二O(n^2)时间复杂度代码相似的速度。
空间复杂度： O(log⁡n)，即为递归需要使用的栈空间。

【2】递归 + 二维前缀和优化： 我们可以对方法一中暴力判定某一部分是否均为0或1的代码进行优化。具体地，当某一部分均为0时，它的和为0；某一部分均为1时，它的和为这一部分的面积大小。我们可以与处理出数组grid的二维前缀和，这样一来，当我们需要判定某一部分是否均为0或1时，可以在O(1)的时间内得到这一部分的和，从而快速地进行判断。

class Solution {public Node construct(int[][] grid) {int n = grid.length;int[][] pre = new int[n + 1][n + 1];for (int i = 1; i <= n; ++i) {for (int j = 1; j <= n; ++j) {pre[i][j] = pre[i - 1][j] + pre[i][j - 1] - pre[i - 1][j - 1] + grid[i - 1][j - 1];}}return dfs(grid, pre, 0, 0, n, n);}public Node dfs(int[][] grid, int[][] pre, int r0, int c0, int r1, int c1) {int total = getSum(pre, r0, c0, r1, c1);if (total == 0) {return new Node(false, true);} else if (total == (r1 - r0) * (c1 - c0)) {return new Node(true, true);}Node ret = new Node(true,false,dfs(grid, pre, r0, c0, (r0 + r1) / 2, (c0 + c1) / 2),dfs(grid, pre, r0, (c0 + c1) / 2, (r0 + r1) / 2, c1),dfs(grid, pre, (r0 + r1) / 2, c0, r1, (c0 + c1) / 2),dfs(grid, pre, (r0 + r1) / 2, (c0 + c1) / 2, r1, c1));return ret;}public int getSum(int[][] pre, int r0, int c0, int r1, int c1) {return pre[r1][c1] - pre[r1][c0] - pre[r0][c1] + pre[r0][c0];}
}

时间复杂度： O(n^2)。在最坏情况下，数组grid中交替出现0和1，此时每一个叶节点对应着1×1的区域。记T(n)为边长为n的数组需要的时间复杂度，那么有：T(n)=4T(n/2)+O(1)以及：T(1)=O(1)根据主定理，可以得到T(n)=O(n^2)。预处理二维前缀和需要的时间也为O(n^2)，因此总时间复杂度为O(n^2)。
空间复杂度： O(n^2)，即为二维前缀和需要使用的空间。