堆的应用
- 1、堆排序
- 2、TopK问题
- 3、堆的相关习题
- 总结
1、堆排序
要学习堆排序,首先要学习堆的向下调整算法,因为要用堆排序,你首先得建堆,而建堆需要执行多次堆的向下调整算法。
但是,使用向下调整算法需要满足一个前提:
若想将其调整为小堆,那么根结点的左右子树必须都为小堆。
若想将其调整为大堆,那么根结点的左右子树必须都为大堆。

向下调整算法的基本思想(大堆):
1.从根结点处开始,选出左右孩子中值较大的孩子。
2.让大的孩子与其父亲进行比较。 若大的孩子比父亲还大,则该孩子与其父亲的位置进行交换。并将原来大的孩子的位置当成父亲继续向下进行调整,直到调整到叶子结点为止。
若大的孩子比父亲小,则不需处理了,调整完成,整个树已经是大堆了。

使用堆的向下调整算法需要满足其根结点的左右子树均为大堆或是小堆才行,那么如何才能将一个任意树调整为堆呢?
答案很简单,我们只需要从倒数第一个非叶子结点开始,从后往前,按下标,依次作为根去向下调整即可。

建堆代码
//建堆for (int i = (n - 1 - 1) / 2; i >= 0; i--){AdjustDown(php->a, php->size, i);}
根据上一弹堆的向下调整算法时间复杂度计算可知,建堆的时间复杂度为O(N)。
那么堆建好后,如何进行堆排序呢?
步骤如下:
1、将堆顶数据与堆的最后一个数据交换,然后对根位置进行一次堆的向下调整,但是调整时被交换到最后的那个最大的数不参与向下调整。
2、完成步骤1后,这棵树除最后一个数之外,其余数又成一个大堆,然后又将堆顶数据与堆的最后一个数据交换,这样一来,第二大的数就被放到了倒数第二个位置上,然后该数又不参与堆的向下调整…反复执行下去,直到堆中只有一个数据时便结束。此时该序列就是一个升序。
为什么升序用到的是大堆呢?
大堆的堆顶是最大的数,可以将其放在数组尾,然后再通过向下调整算法找到次大的数。而小堆的堆顶是最小的数,需要放在第一个位置,如果用原来的堆找不到次小的数,而重新建堆则会更加繁琐。
堆排序实现
//升序 大堆
void HeapSort(int arr[], int size)
{assert(arr);//1.建堆 向上调整 O(N*logN)//for (int i = 1; i < size; i++)//{// AdjustUp(arr, i);//}//1.向下调整建堆 O(N)//从第一个非叶子结点开始向下调整,一直到根for (int i = (size - 1 - 1) / 2; i >= 0; i--){AdjustDown(arr, size, i);}//2.向下调整 O(N*logN)int end = size - 1;//记录堆的最后一个数据的下标while (end > 0){Swap(&arr[0], &arr[end]);//将堆顶的数据和堆的最后一个数据交换AdjustDown(arr, end, 0);//对根进行一次向下调整end--;//堆的最后一个数据的下标减一}
}
2、TopK问题
TOP-K问题:即求数据结合中前K个最大的元素或者最小的元素,一般情况下数据量都比较大。
比如:专业前10名、世界500强、富豪榜、游戏中前100的活跃玩家等。
对于Top-K问题,能想到的最简单直接的方式就是排序,但是:如果数据量非常大,排序就不太可取了(可能
数据都不能一下子全部加载到内存中)。最佳的方式就是用堆来解决,基本思路如下:
1. 用数据集合中前K个元素来建堆
前k个最大的元素,则建小堆
前k个最小的元素,则建大堆
2. 用剩余的N-K个元素依次与堆顶元素来比较,不满足则替换堆顶元素
将剩余N-K个元素依次与堆顶元素比完之后,堆中剩余的K个元素就是所求的前K个最小或者最大的元素。
假设我们要找出10亿个随机数中的前k个最大的数。
假设数据类型为int,那么占用的内存是多少?
1GB=1024MB
1MB=1024Kb
1KB=1024Byte
10亿个数则是10亿字节,40亿Byte=3,906,250KB=3,814.697MB=3.725GB
因为内存的空间是有限的,所以在处理这么大内存的数据时,我们需要用到文件处理。
为了让速度较快一些,我们就假设在一千万个随机数中求前K个数。
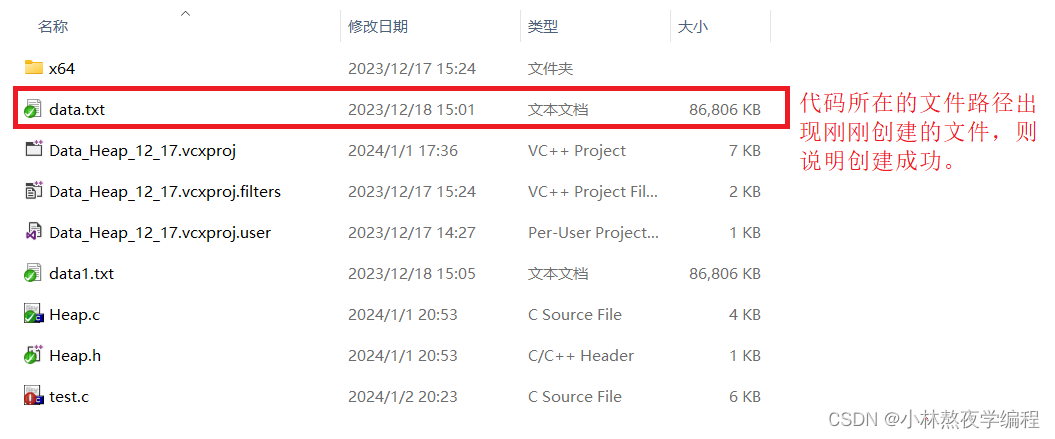
1、我们需要创建一个有一万个数的文件。
此处我们需要用到两个文件处理函数和文件打开关闭函数。
//文件打开
FILE * fopen ( const char * filename, const char * mode );//前面参数为文件名 后面参数为文件打开方式
//文件关闭
int fclose ( FILE * stream );
int fprintf ( FILE * stream, const char * format, ... );//将后面函数写入的信息写入stream
int fscanf ( FILE * stream, const char * format, ... );//将stream的信息写入后面的函数
创建随机值,需要用到srand(),但是随机数的范围为0-32767。最多只有32768个,远小于一千万,为了减少随机输的重复,我们需要将随机数加上一个数。单纯的使用srand不是真正的随机时,这些我们需要用到时间这个参数,使它为真正的随机数。srand的头文件是#include<stdlib.h>。time的头文件是#include<time.h>。
srand((unsigned int)time(NULL));
代码实现
//1.创造随机数到文件中
void CreateNDate()
{int n = 10000000;srand((unsigned int)time(NULL));FILE* pf = fopen("data.txt", "w");//以写的方式打开文件if (pf == NULL){perror("fopen fail");return;}for (int i = 0; i < n; i++){//rand随机数有限制 只有几万个 所以+iint x = (rand() + i) % 10000000;fprintf(pf, "%d\n", x);//将数据写入文件中}fclose(pf);//关闭文件pf = NULL;//手动置空
}
测试

2、 用数据集合中前K个元素来建堆,用剩余的N-K个元素依次与堆顶元素来比较,不满足则替换堆顶元素
此处找最大的前k个,建小堆。
建小堆大的数据才能进来,最后留下的也是大的数据。
建大堆则只能进来小的数据,不符合题意。
2.1、打开文件
//打开文件
FILE* pf = fopen("data.txt", "r");
if (pf == NULL)
{perror("fopen error");return;
}2.2、读取文件并将前k个数据创建小堆
int* minheap = (int*)malloc(sizeof(int) * k);
if (minheap == NULL)
{perror("malloc fail");return;
}
//1.读取文件前k个建小堆
for (int i = 0; i < k; i++)
{fscanf(pf, "%d", &minheap[i]);AdjustUp(minheap, i);
}
2.3、用剩余的N-K个元素依次与堆顶元素来比较
//2.读取文件的数据与堆顶数据进行比较 如果大则 向下调整
int x = 0;
while (fscanf(pf, "%d", &x) != EOF)
{if (x > minheap[0]){minheap[0] = x;AdjustDown(minheap, k, 0);}
}
2.4、将前k个数据打印出来并关闭文件
for (int i = 0; i < k; i++)
{printf("%d ", minheap[i]);
}
free(minheap);
fclose(pf);
pf = NULL;
测试
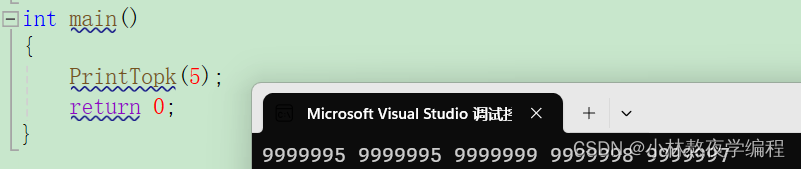
虽然我们打印出了前k大值,那我们怎么知道这个算法就是对的呢?
此处博主的解决办法是修改文件中的k个值,改为都是超过一千万的值,如果打印出来的K个值是修改的值,那么此算法就是正确的。

经过修改打印出来的就是修改的值,说明算法没有问题。此处如果需要升序或者降序打印,进行一个排序算法即可。
3、堆的相关习题
1.下列关键字序列为堆的是:()
A 100,60,70,50,32,65
B 60,70,65,50,32,100
C 65,100,70,32,50,60
D 70,65,100,32,50,60
E 32,50,100,70,65,60
F 50,100,70,65,60,32

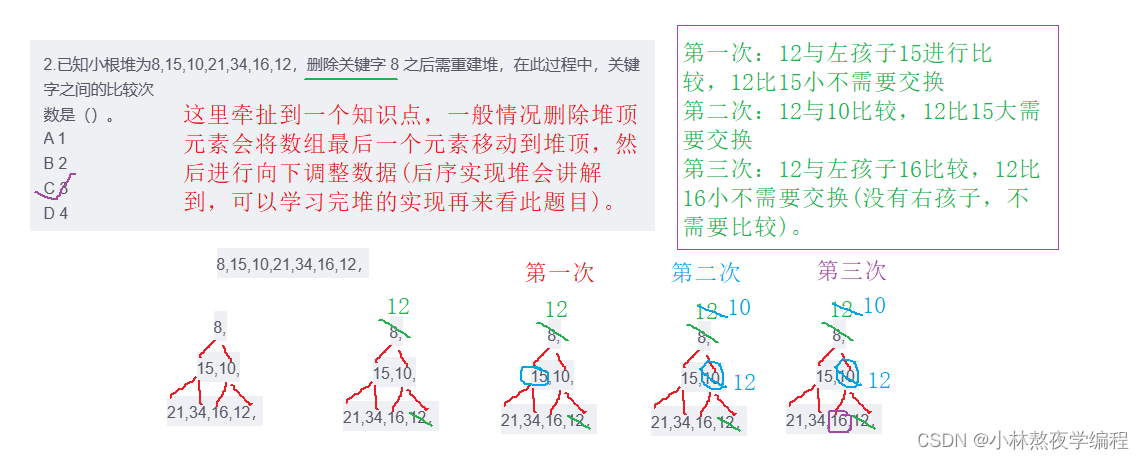
2.已知小根堆为8,15,10,21,34,16,12,删除关键字 8 之后需重建堆,在此过程中,关键字之间的比较次
数是()。
A 1
B 2
C 3
D 4
3.一组记录排序码为(5 11 7 2 3 17),则利用堆排序方法建立的初始堆为
A(11 5 7 2 3 17)
B(11 5 7 2 17 3)
C(17 11 7 2 3 5)
D(17 11 7 5 3 2)
E(17 7 11 3 5 2)
F(17 7 11 3 2 5)

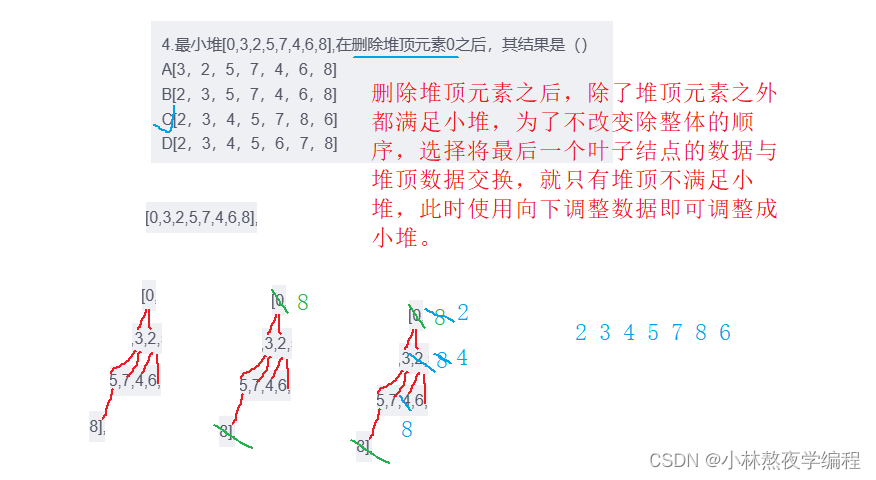
4.最小堆[0,3,2,5,7,4,6,8],在删除堆顶元素0之后,其结果是()
A[3,2,5,7,4,6,8]
B[2,3,5,7,4,6,8]
C[2,3,4,5,7,8,6]
D[2,3,4,5,6,7,8]
总结
本篇博客就结束啦,谢谢大家的观看,如果公主少年们有好的建议可以留言喔,谢谢大家啦!

圆、直线)

---Mysql多版本共存(Mac系统))















)