在接下来的几章中,我们将讨论一组重要的并行计算模式。这些模式是许多并行应用中出现的广泛并行算法的基础。我们将从卷积开始,这是一种流行的阵列操作,以各种形式用于信号处理、数字记录、图像处理、视频处理和计算机视觉。在这些应用领域,卷积通常作为过滤器执行,将信号和像素转换为更理想的值。我们的图像模糊内核是一个过滤器,可以平滑信号值,以便人们可以看到大画面的趋势。另一个例子是,高斯滤波器是卷积滤波器,可用于锐化图像中对象的边界和边缘。
在高性能计算中,卷积模式通常被称为模板计算,这在求解微分方程的数值方法中广泛出现。它还构成了模拟模型中许多力计算算法的基础。卷积通常涉及每个数据元素上的大量算术运算。对于高清图像和视频等大型数据集,计算量可能非常大。每个输出数据元素都可以相互独立计算,这是并行计算的理想特征。另一方面,在具有一定挑战性的边界条件的输出数据元素之间有相当程度的输入数据共享。这使得卷积成为复杂的tile方法和输入数据暂存方法的重要用例。
7.1 BACKGROUND
卷积是一种数组操作,其中每个输出数据元素是相邻输入元素集合的加权和。加权和计算中使用的权重由输入掩码数组定义,通常称为卷积内核。由于CUDA内核函数和卷积内核之间存在不幸的名称冲突,我们将这些掩码数组称为卷积掩码,以避免混淆。相同的卷积掩码通常用于数组的所有元素。

在音频数字信号处理中,输入数据为ID形式,并表示采样信号量作为时间函数。图7.1显示了1D数据的卷积示例,其中5元卷积掩码数组M应用于7元输入数组N。我们将遵循C语言惯例,其中N和P元素从0到6索引,M元素从0到4索引。我们使用5元素掩码M的事实意味着每个P元素是由对应位置的N个元素的加权和生成的,左边是两个N个元素,右边是两个N个元素。
例如, P[2] 的值生成为 N[0](即 N[2-2])到N[4](即N[2+2])的加权和。在这个例子中,我们任意假设N个元素的值是1,2,3,…,7。M元素定义了权重,在本例中,其值为3、4、5、4、3。在将乘积加在一起之前,每个权重值乘以相应的N个元素值。如图7.1所示,P[2]的计算如下:

通常,掩码的大小往往是一个奇数,这使得加权和计算围绕正在计算的元素是对称的。也就是说,一个奇数的掩码元素定义了加权和,以包括被计算元素两侧相同数量的元素。在图7.1,掩码尺寸是5。每个输出元素计算为相应输入元素、左侧两个元素和右侧两个元素的加权和。

在图7.1中,P[i] 的计算可以看作是从 N[i-2] 开始的N子数组和M数组之间的内积。图7.2显示了P[3]的计算。计算由一个N个元素从图7.1.中的N个元素移动。也就是说,P[3] 的值是N[1](即N[3-2])通过N[5](即N[3 + 2])的加权和。
我们可以认为 P[3] 的计算如下:
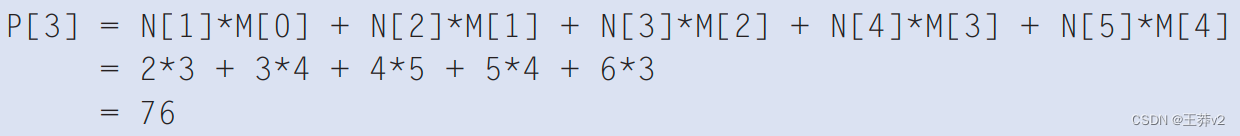
由于卷积是根据相邻元素定义的,因此接近数组末端的输出元素自然会出现边界条件。如图7.3所示,当我们计算P[1]时,N[1]左边只有一个N个元素。也就是说,根据我们的卷积定义,没有足够的N个元素来计算P[1]。处理此类边界条件的典型方法是定义这些缺失的N个元素的默认值。对于大多数应用程序,默认值是0,这是我们在图7.3.中使用的。例如,在音频信号处理中,我们可以假设信号音量在录制开始前和结束后为0。在这种情况下,P[1]的计算如下:
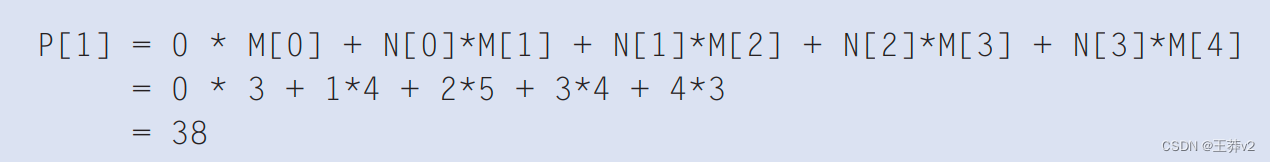
此计算中不存在的N元素在图7.3.中显示为虚数框。应该清楚的是,P[0]的计算将涉及两个缺失的N个元素,在本例中,这两个元素都将被假定为0。我们把P[0]的计算作为练习。这些缺失的元素在文献中通常被称为“ghost cells”或“halo cells”。由于在并行计算中使用 tile,还有其他类型的 ghost cells。这些幽灵细胞可以对tile的有效性和/或效率产生重大影响。我们很快就会回到这一点上。

此外,并非所有应用程序都假设幽灵单元格包含0。例如,一些应用程序可能会假设幽灵单元格包含与最接近的有效数据元素相同的值。
对于图像处理和计算机视觉,输入数据通常是二维数组,像素在x-y空间中。因此,图像卷积是二维卷积,如图7.4.所示。在二维卷积中,掩码M是一个二维数组。它的x和y维度决定了加权和计算中要包含的邻居的范围。在图7.4中,为了简单起见,我们使用5×5的掩码。总的来说,掩码不一定是正方形数组。要生成输出元素,我们取中心位于输入数组N中相应位置的子数组。然后,我们在掩码数组的元素和图像数组的元素之间进行成对乘法。在我们的示例中,结果显示为图7.4.中N和P下方的5×5乘积数组。输出元素的值是乘积数组所有元素的总和。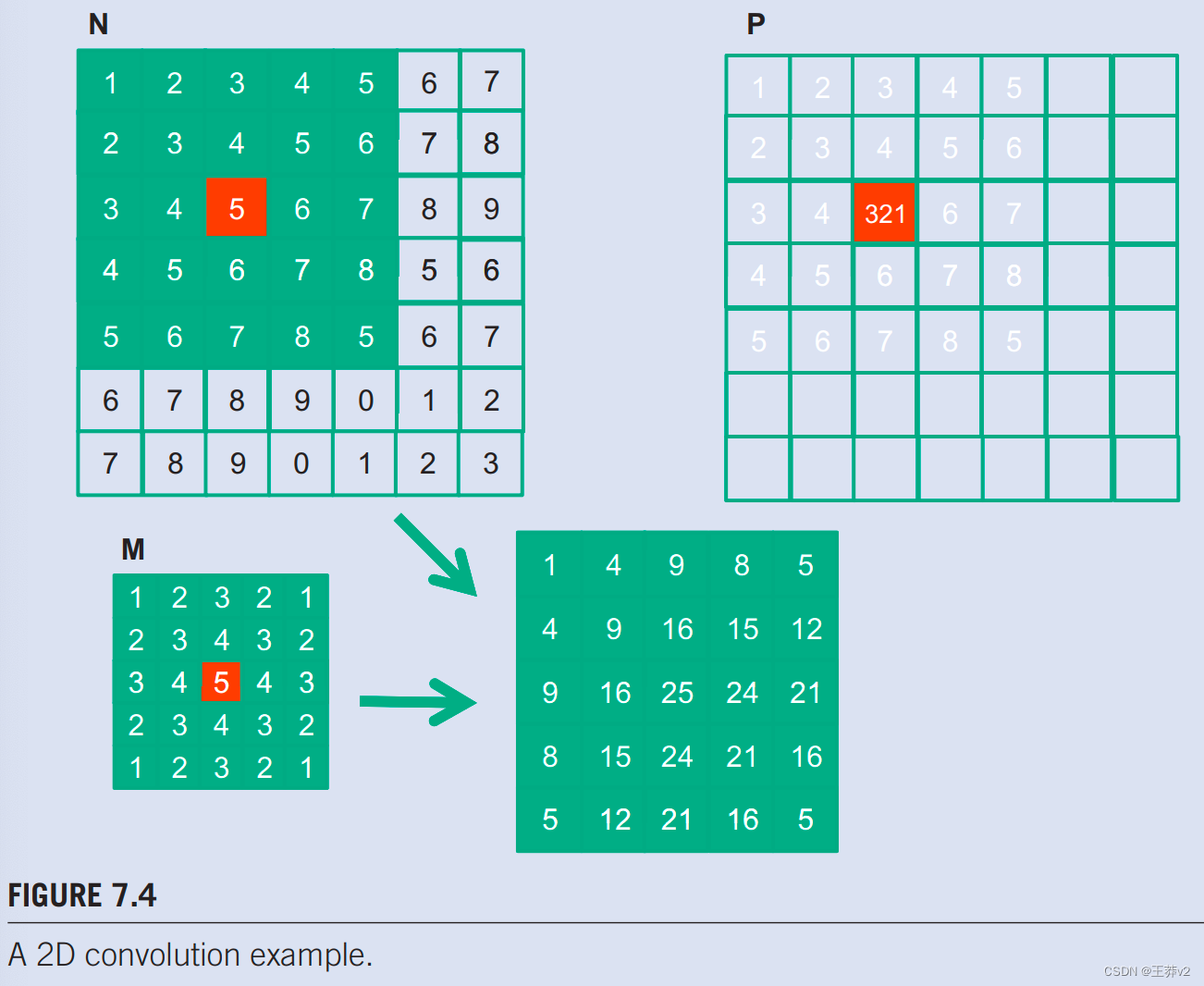
图7.4中的例子。显示了 P 2.2 P_{2.2} P2.2的计算。为了简洁,我们将使用Ny.x在寻址C数组时表示N[y][x]。由于N和P很可能是动态分配的数组,我们将在实际代码示例中使用线性化索引。N的子数组用于计算P2.2的值,在x或水平方向上从N0.0到N0.4,在y或垂直方向上从N0.0到N4.0。计算方法如下:
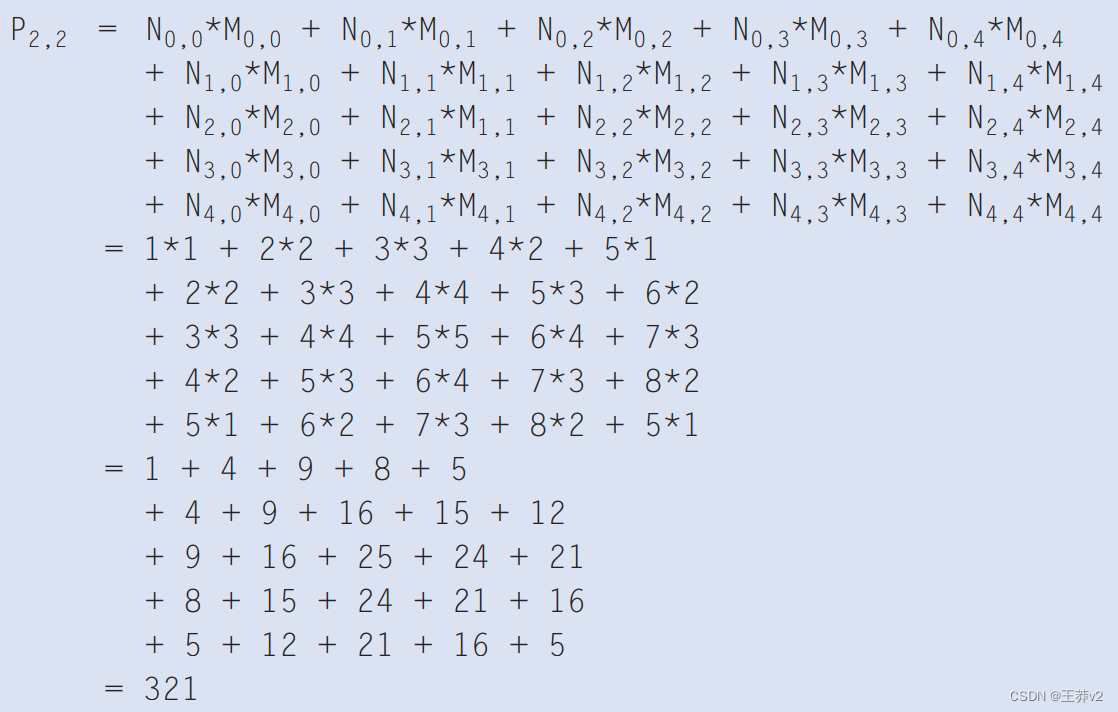
与1D卷积一样,2D卷积也必须处理边界条件。对于x和y维度的边界,有更复杂的边界条件:输出元素的计算可能涉及沿水平边界、垂直边界或两者的边界条件。图7.5说明了涉及两个边界的P元素的计算。来自图7.5,P1.0 的计算涉及N子数组中缺少两列和一个缺失的水平行。与1D卷积一样,不同的应用程序对这些缺失的N个元素假设不同的默认值。在我们的示例中,我们假设默认值为0。这些边界条件也会影响瓷砖的效率。我们很快就会回到这一点上。













)

)


 .net core实现分片上传)
)